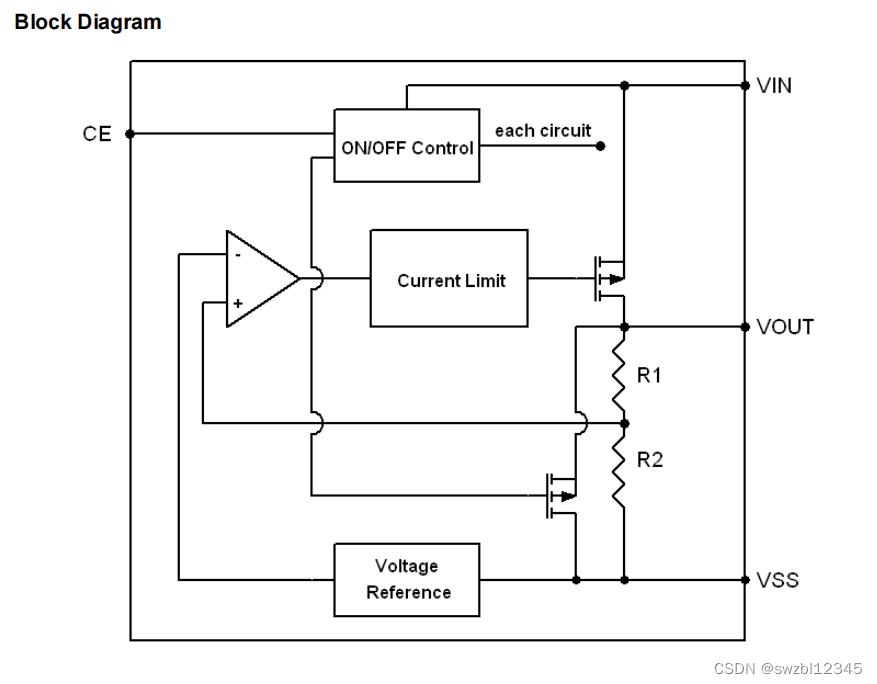
LSM Tree 的存储模型，包括 Tidb，HBase等

特点

通过将大量的随机写转换为顺序写，从而极大地提升了数据写入的性能，虽然与此同时牺牲了部分读的性能。

只适合存储 key 值有序且写入大于读取的数据，或者读取操作通常是 key 值连续的数据。

存储模型

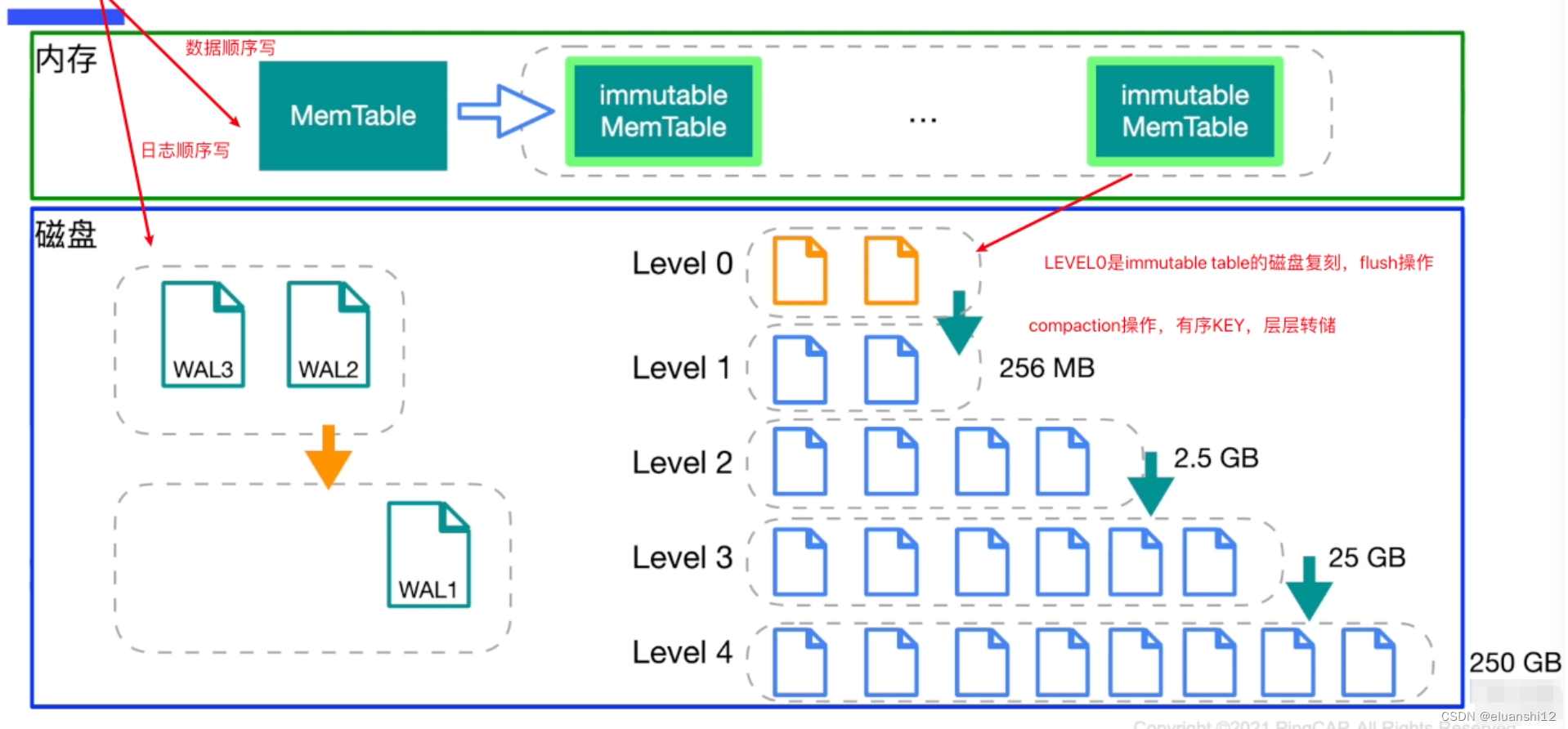
WAL

在设计数据库的时候经常被使用，当插入数据时，先顺序写入 WAL 文件中，之后插入到内存中的 MemTable 中。
1.保证了数据的持久化，不会丢失数据，并且都是顺序写，速度很快。
2.当程序挂掉重启时，可以从 WAL 文件中重新恢复内存中的 MemTable。

MemTable

MemTable 对应的就是 WAL 文件在内存中的存储结构，通常用 跳跃表SkipList 来实现。MemTable 提供了 k-v 数据的写入、删除以及读取的操作接口。其内部将 k-v 对按照 key 值有序存储，这样方便之后快速序列化到 SSTable 文件中，仍然保持数据的有序性。

为了维持有序性在内存里面可以采用红黑树或者跳跃表相关的数据结构。

Immutable Memtable

在内存中只读的 MemTable，由于内存是有限的，通常我们会设置一个阀值，当 MemTable 占用的内存达到阀值后就自动转换为 Immutable Memtable，Immutable Memtable 是只读不写的，系统此时会生成新的 MemTable 供写操作继续写入。

之所以要使用 Immutable Memtable，就是为了避免将Immutable MemTable 中的内容序列化到磁盘中时会阻塞写操作。

为什么LSM不直接顺序写入磁盘，而是需要在内存中缓冲一下？
单条写的性能肯定没有批量写来的块。例如kafka给我们的感觉是写入后就落地，但其实并不是，可以根据条数或者时间比如200ms刷入磁盘一次，这样能大大提升写入效率。此外在LSM中，在磁盘缓冲的另一个好处是，针对新增的数据，可以直接查询返回，能够避免一定的IO操作。

SSTable（Sorted String Table）

SSTable 就是Immutable MemTable 中的数据在磁盘上的有序存储，其内部数据是根据 key 从小到大排列的。通常为了加快查找的速度，需要在 SSTable 中加入数据索引，可以快读定位到指定的 k-v 数据。

SSTable 通常采用的分级的结构（默认至多 6 层）。Immutable MemTable 中的数据达到指定阀值后会在 Level 0 层创建一个新的 SSTable。每一层的数据达到一定阈值后会挑选一部分 SST 合并到下一层（旧的文件删除），每一层的数据是上一层的 10 倍（因此 90% 的数据存储在最后一层）。
SSTable 中的 k-v 数据都是有序的，相当于是多路归并排序（Merge sort），合并操作相当快速。

L0层的SSTable是没有进行合并的，所以这里的key range在多个SSTable中可能会出现重叠，在层数大于0层之后的SSTable，不存在重叠key。

（Minor/Major Compaction：
Minor Compaction：Memtable到SSTable层；
Major Compaction：当每层的磁盘上的SSTable的体积超过一定的大小或者个数，也会周期的进行合并。清除掉被标记删除掉的数据以及多版本数据的合并，避免浪费空间）

更新

更新操作其实并不真正存在，和写入一个 k-v 数据没有什么不同，只是在读取的时候，会从 Level0 层的 SSTable 文件开始查找数据，数据在上层的 SSTable 文件中必然比下层的文件中要新，所以总能读取到最新的那条数据。也就是说此时在整个 LSM Tree 中可能会同时存在多个 key 值相同的数据，只有在之后合并 SSTable 文件的时候，才会将旧的值删除。

删除

删除一条记录的操作比较特殊，并不立即将数据从文件中删除，而是记录下对这个 key 的删除操作标记，同插入操作相同，插入操作插入的是 k-v 值，而删除操作插入的是 k-del 标记，只有当合并 SSTable 文件时才会真正的删除。

合并Compaction（size-tiered和leveled）

当数据不断从 Immutable Memtable 序列化到磁盘上的 SSTable 文件中时，SSTable 文件的数量就不断增加，而且其中可能有很多更新和删除操作并不立即对文件进行操作，而只是存储一个操作记录，这就造成了整个 LSM Tree 中可能有大量相同 key 值的数据，占据了磁盘空间。为了节省磁盘空间占用，控制 SSTable 文件数量，需要将多个 SSTable 文件进行合并，生成一个新的 SSTable 文件。

1）读放大:读取数据时实际读取的数据量大于真正的数据量。例如在LSM树中需要先在MemTable查看当前key是否存在，不存在继续从SSTable中寻找。
2）写放大:写入数据时实际写入的数据量大于真正的数据量。例如在LSM树中写入时可能触发Compact操作，导致实际写入的数据量远大于该key的数据量。
3）空间放大:数据实际占用的磁盘空间比数据的真正大小 大更多。冗余存储，对于一个key来说，只有最新的那条记录是有效的，而之前的记录都是可以被清理回收的。

1) size-tiered 策略

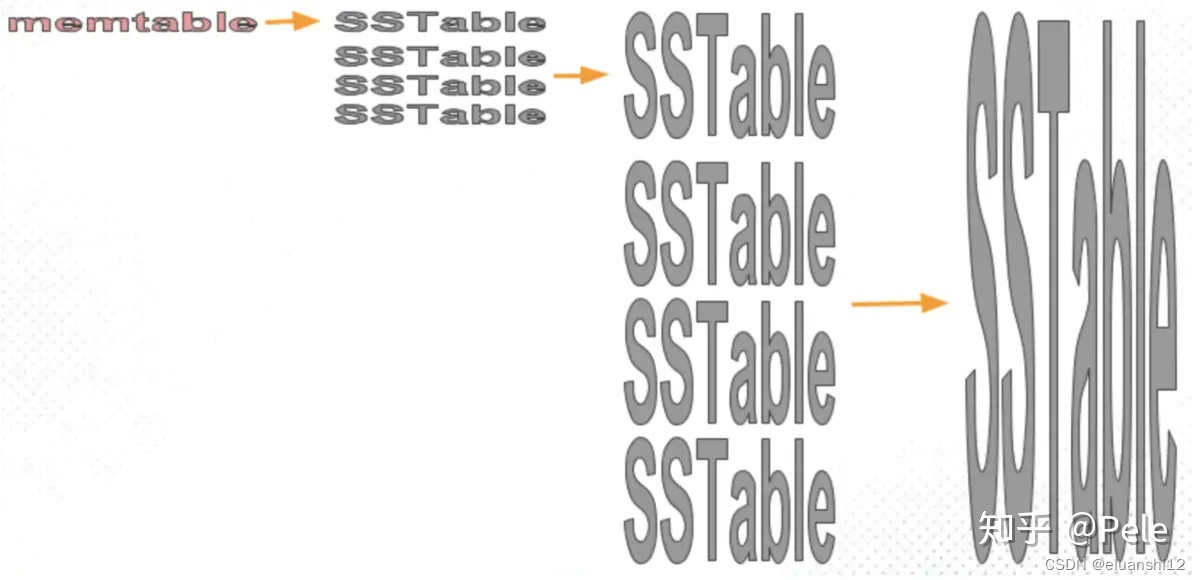
保证每层SSTable的大小相近，同时限制每一层SSTable的数量。如上图，每层限制SSTable为N，当每层SSTable达到N后，则触发Compact操作合并这些SSTable，并将合并后的结果写入到下一层成为一个更大的sstable。

由此可以看出，当层数达到一定数量时，最底层的单个SSTable的大小会变得非常大。并且size-tiered策略会导致空间放大比较严重。即使对于同一层的SSTable，每个key的记录是可能存在多份的，只有当该层的SSTable执行compact操作才会消除这些key的冗余记录。

2) leveled策略

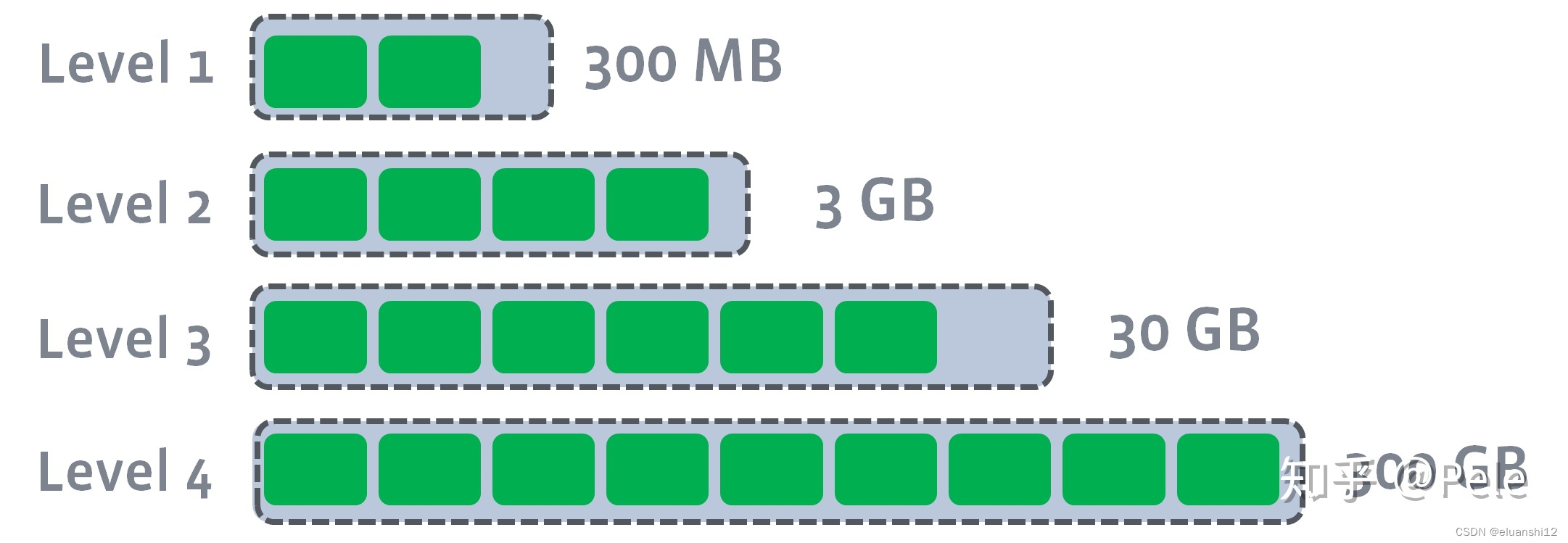每一层的总大小固定，从上到下逐渐变大
采用分层思想，每一层限制总文件的大小。
将每一层切分成多个大小相近的SSTable。这些SSTable是这一层是全局有序的。
知乎-LSM树详解

读取

LSM Tree 的读取效率并不高，当需要读取指定 key 的数据时，

1. 先在内存中的 MemTable 和 Immutable MemTable 中查找，查询到就返回。
2. 如果没有找到，则从 Level 0 层开始依次下沉，直到把所有的Level层查询一遍得到最终结果，如果查找失败，说明整个 LSM Tree 中都不存在这个 key 的数据。如果中间在任何一个地方找到这个 key 的数据，那么按照这个路径找到的数据都是最新的。

在每一层的 SSTable 文件的 key 值范围是不重复的，所以只需要查找其中一个 SSTable 文件即可确定指定 key 的数据是否存在于这一层中。Level 0 层比较特殊，因为数据是 Immutable MemTable 直接写入此层的，所以 Level 0 层的 SSTable 文件的 key 值范围可能存在重复，查找数据时有可能需要查找多个文件。

优化读取

因为这样的读取效率非常差，通常会进行一些优化，例如 LevelDB 中的 Mainfest 文件，这个文件记录了 SSTable 文件的一些关键信息，例如 Level 层数，文件名，最小 key 值，最大 key 值等，这个文件通常不会太大，可以放入内存中，可以帮助快速定位到要查询的 SSTable 文件，避免频繁读取。
另外一个经常使用的方法是布隆解析器(Bloom filter)，布隆解析器是一个使用内存判断文件是否包含一个关键字的有效方法。对每一个 SSTable 添加 Bloom Filter。
压缩
SSTable 是可以启用压缩功能的，并且这种压缩不是将整个 SSTable 一起压缩，而是根据 locality 将数据分组，每个组分别压缩，这样的好处当读取数据的时候，我们不需要解压缩整个文件而是解压缩部分 Group 就可以读取。
缓存
因为SSTable在写入磁盘后，除了Compaction之外，是不会变化的，所以我可以将Scan的Block进行缓存，从而提高检索的效率
合并

B+Tree VS LSM-Tree

数据拆分

LSM-Tree的设计思路是，将数据拆分为几百M大小的Segments（SSTable），并是顺序写入。
B+Tree则是将数据拆分为固定大小的Block或Page, 一般是4KB大小，和磁盘一个扇区的大小对应，Page是读写的最小单位。

更新

在数据的更新和删除方面，B+Tree可以做到原地更新和删除，这种方式对数据库事务支持更加友好，因为一个key只会出现一个Page页里面。
LSM-Tree只能追加写，并且在L0层key的rang会重叠，所以对事务支持较弱，只能在Segment Compaction的时候进行真正地更新和删除。

读写

LSM-Tree的优点是支持高吞吐的写（可认为是O（1）），这个特点在分布式系统上更为看重，当然针对读取普通的LSM-Tree结构，读取是O（N）的复杂度，在使用索引或者缓存优化后的也可以达到O（logN）的复杂度。
而B+tree的优点是支持高效的读（稳定的O（logN）），但是在大规模的写请求下（复杂度O(LogN)），效率会变得比较低，因为随着insert的操作，为了维护B+树结构，节点会不断的分裂和合并。操作磁盘的随机读写概率会变大，故导致性能降低。

基于LSM-Tree分层存储能够做到写的高吞吐，带来的副作用是整个系统必须频繁的进行compaction，写入量越大，Compaction的过程越频繁。而compaction是一个compare & merge的过程，非常消耗CPU和存储IO，在高吞吐的写入情形下，大量的compaction操作占用大量系统资源，必然带来整个系统性能断崖式下跌，对应用系统产生巨大影响，当然我们可以禁用自动Major Compaction，在每天系统低峰期定期触发合并，来避免这个问题。

总结

LSM Tree 的思想非常实用，将随机写转换为顺序写来大幅提高写入操作的性能，但是牺牲了部分读的性能。