三、栈、队列和数组
目录
- 三、栈、队列和数组
- 栈
- 基本概念
- 顺序栈
- 链式栈
- 队列
- 基本概念
- 顺序存储
- 链式存储
- 双端队列
- 应用
- 括号匹配
- 前中后缀表达式
- 栈在递归中的运用
- 队列的运用
- 数组
- 数组的存储
- 对称矩阵
- 三角矩阵
- 三对角矩阵
- 稀疏矩阵
栈
基本概念
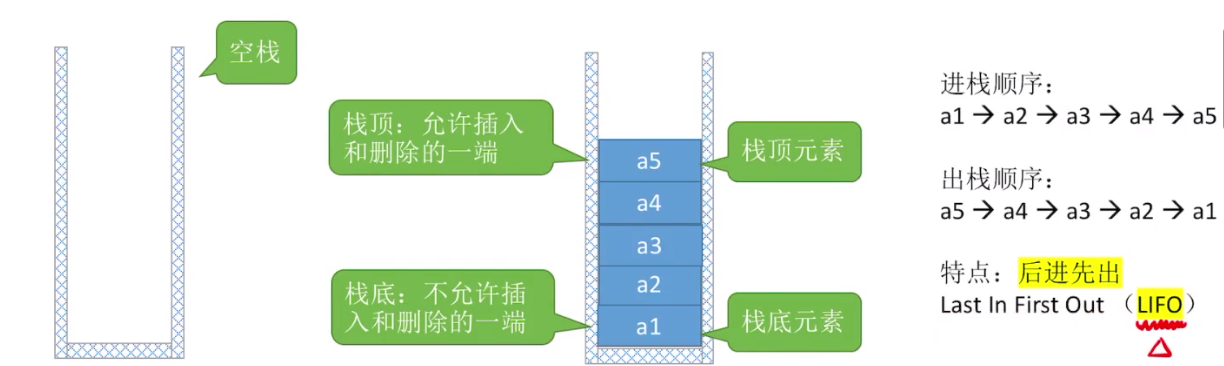
栈是只允许在一端进行插入或删除操作的线性表。
- 栈顶:线性表允许进行插入删除的那一端
- 栈底:固定的,不允许进行插入删除的那一端
- 空栈:不含任何元素的空表
特点:先进后出
基本操作:

常考题型:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-yAQLivaR-1686635232177)(null)]
顺序栈
结构体:
//结构体
#define MaxSize 10 //定义栈中元素的最大个数
typedef struct
{
int data[MaxSize];//静态数组存放栈中元素
int top;//栈顶指针
} SqStack;
初始化:
//初始化
void InitStack(SqStack& S)
{
S.top = -1;//初始化栈顶指针 若为0.则指向下一个插入的位置
}
判空:
//判空
bool StackEmpty(SqStack S)
{
if (S.top == -1) return true;//判空
else return false;
}
进栈:
//进栈
bool Push(SqStack& S, int x)
{
if (S.top == MaxSize - 1)//栈满,报错
return false;
S.top = S.top + 1;//先加1
S.data[S.top] = x;//新元素入栈 这两行等价于S.data[++S.top]=x;
return true;
}
出栈:
//出栈
bool Pop(SqStack& S, int& x)
{
if (S.top == -1) return false;//栈空,报错
x = S.data[S.top];//栈顶元素先出栈
S.top = S.top - 1;//指针再减一 这两行等价于 x=S.data[S.top--]
return true;
}
获取栈顶元素:
//读取栈顶元素
bool GetTop(SqStack& S, int& x)
{
if (S.top == -1) return false;//栈空,报错
x = S.data[S.top];//栈顶元素出栈
return true;
}
让top指向待插入位置的写法:(初始化top=0)

缺点:栈的大小不可变
可以使用共享栈进行优化,提高内存运用率。

共享栈定义:
//共享栈
typedef struct
{
int data[MaxSize]; //静态数组存放栈中元素
int top0; //0号栈栈顶指针
int top1; //1号栈栈顶指针
} ShStack;
//初始化共享栈
void InitStack(ShStack& S)
{
S.top0 = -1;
S.top1 = MaxSize;
//栈满条件为top0+1==top1
}
链式栈
链式栈的构建和单链表十分相似,主要限制与进栈出栈都只能在栈顶一端进行(链头作为栈顶)
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Qpnymbqf-1686635230993)(null)]
结构体:
# define MaxSize 10
typedef struct LinkNode {
int data;
struct LinkNode* next;
} *LinkStack;
初始化:
//初始化
bool InitStack(LinkStack& LS) {
LS = (LinkNode*)malloc(sizeof(LinkNode));//分配一个头节点
if (LS == NULL) {
return false;
}
LS->next = NULL;
return true;
}
入栈:
//入栈
bool Push(LinkStack& LS, int t) {
LinkNode* s = (LinkNode*)malloc(sizeof(LinkNode));
if (s == NULL)return false;
s->data = t;
s->next = LS->next;
LS->next = s;
return true;
}
出栈:
//出栈
bool Pop(LinkStack& LS, int& x) {
//判断
if (LS->next == NULL)return false;//栈空,这里的条件
LinkNode* q;
q = LS->next;
LS->next = q->next;
x = q->data;
free(q);
return true;
}
获取栈顶元素:
//获取栈顶元素
bool GetTop(LinkStack LS, int& x) {
if (LS == NULL)return false;
x = LS->next->data;
return true;
}
队列
基本概念
队列是只允许在一端进行插入,在另一端删除操作的线性表。(分别称为入队,出队)
- 特点:先进先出,后进后出(FIFO)
- 队头:允许删除的一端
- 队尾:允许插入的一端
基本操作:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Do0UhQza-1686635229210)(C:\Software\PicGo\1683358362151.png)]
顺序存储
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-pZhiTig2-1686635230819)(null)]
结构体:
#define MaxSize 10 //定义队列中元素的最大个数
typedef struct
{
int data[MaxSize];//用静态数组存放队列元素、
int front, rear;//队头指针和队尾指针
} SqQueue;
初始化:
//初始化队列
void InitQueue(SqQueue& Q)
{
//初始,队头队尾指针指向0
Q.front = Q.rear = 0;//队尾指针始终指向下一个插入的位置
}
判空:
//判空
bool QueueEmpty(SqQueue Q)
{
if (Q.rear == Q.front) return true;
else return false;
}
入队:
//入队
bool EnQueue(SqQueue& Q, int x)
{
if ((Q.rear+1)%MaxSize==Q.front)//判断队满
return false;
Q.data[Q.rear] = x;
Q.rear = (Q.rear + 1)%MaxSize;//队尾指针加1取模,以循环队列的形式进行存储
}
出队:
//出队
bool DeQueue(SqQueue& Q, int& x)
{
if (Q.rear == Q.front)//判空
return false;
x = Q.data[Q.front];
Q.front = (Q.front + 1) % MaxSize;//队头后移
return true;
}
获取队头元素:
//获取队头元素
bool GetHead(SqQueue& Q, int& x)
{
if (Q.rear == Q.front)//判空
return false;
x = Q.data[Q.front];
return true;
}
判断队满的三种方式:
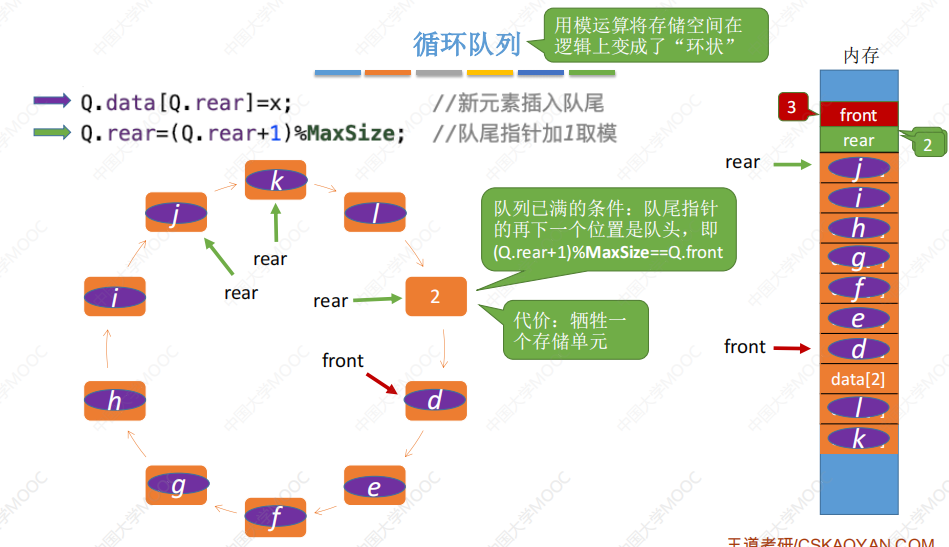
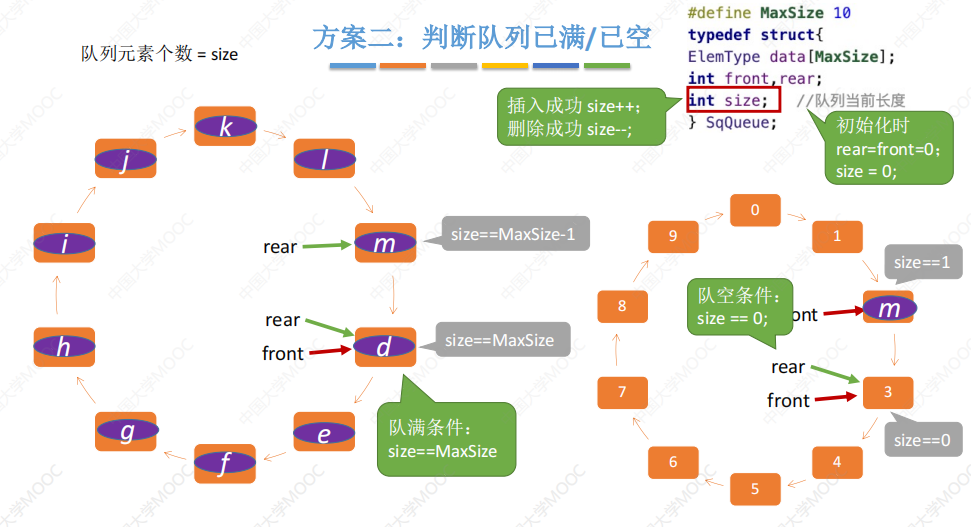
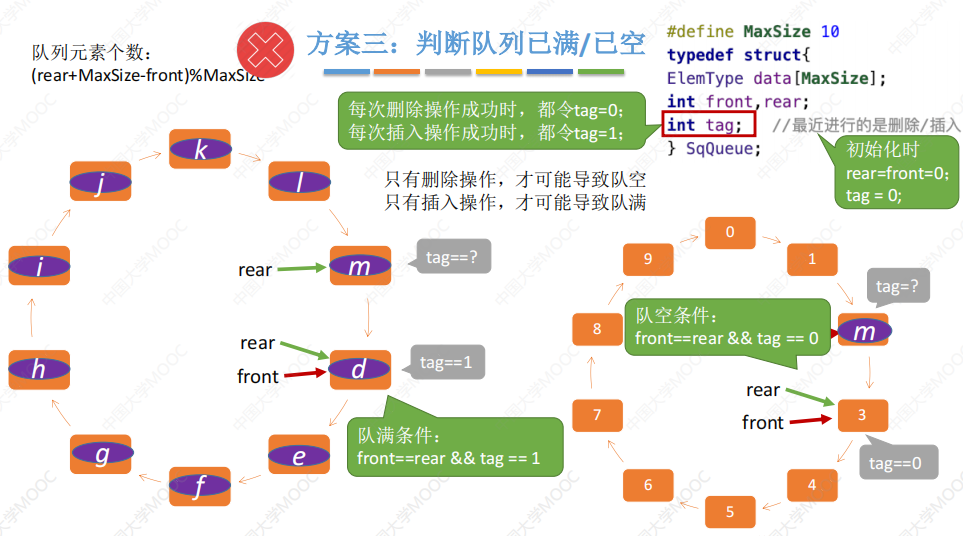
对于rear和front指针的初始化方式可能会有所不同,由此会有不同的出题方式。
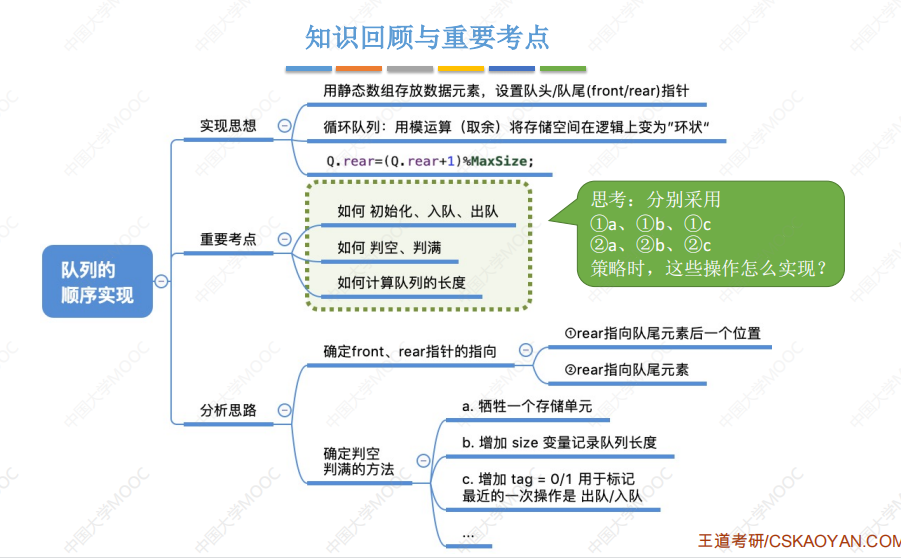
链式存储
以下为带头结点的链式队列:
结构体:
//结构体
typedef struct LinkNode
{
int data;
struct LinkNode* next;
}LinkNode;
typedef struct
{
LinkNode* front, * rear;//队头队尾指针
}LinkQueue;
初始化:
//初始化
void InitQueue(LinkQueue& Q)
{
//初始时 front、rear都指向头结点
Q.front = Q.rear = (LinkNode*)malloc(sizeof(LinkNode));
Q.front->next = NULL;
}
判空:
//判空
bool IsEmpty(LinkQueue Q)
{
if (Q.front == Q.rear)
return true;
else return false;
}
入队:
//入队
void EnQueue(LinkQueue& Q, int x)
{
LinkNode* s = (LinkNode*)malloc(sizeof(LinkNode));
s->data = x;
s->next = NULL;
Q.rear->next = s;//新节点插入到rear后面
Q.rear = s;//修改表尾指针
}
出队:出队时需要进行特判,当出队元素为最后一个结点时,需要修改rear指针。
//出队
bool DeQueue(LinkQueue& Q, int& x)
{
if (Q.front == Q.rear) return false;//判空
LinkNode* p = Q.front->next;
x = p->data;//用变量x返回队头元素
Q.front->next = p->next;//修改头结点的next指针
if (Q.rear == p)//此次是最后一个结点出队
Q.rear = Q.front;//修改rear指针
free(p);//释放结点空间
return true;
}
以下是不带头结点的链式队列:
初始化:
//初始化(不带头结点)
void InitQueue2(LinkQueue& Q)
{
//初始时,front、rear都指向NULL
Q.front = NULL;
Q.rear = NULL;
}
判空:
//判空(不带头结点)
bool IsEmpty2(LinkQueue Q)
{
if (Q.front == NULL) return true;
else return false;
}
入队:
//入队(不带头结点)
void EnQueue2(LinkQueue& Q, int x)
{
LinkNode* s = (LinkNode*)malloc(sizeof(LinkNode));
s->data = x;
s->next = NULL;
if (Q.front == NULL)//在空序列中插入第一个元素
{
Q.front = s;
Q.rear = s;
}
else
{
Q.rear->next = s;
Q.rear = s;
}
}
出队:
//出队(不带头结点)
bool DeQueue2(LinkQueue& Q, int& x)
{
if (Q.front == NULL) return false;
LinkNode* p = Q.front;//p指向此次出队的结点
x = p->data;//用变量x返回队头元素
Q.front = p->next;//修改front指针
if (Q.rear == p)//此次是最后一个结点出队
{
Q.front = NULL;
Q.rear = NULL;
}
free(p);//释放结点
}
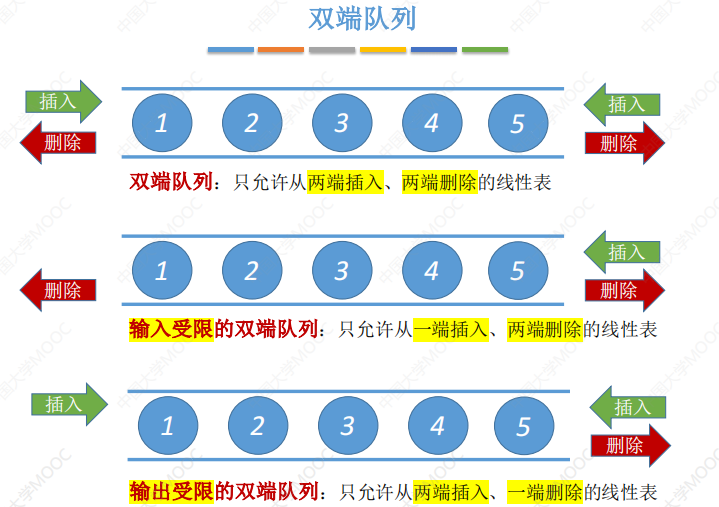
双端队列
双端队列是指两端都可以进行入队和出队操作的队列
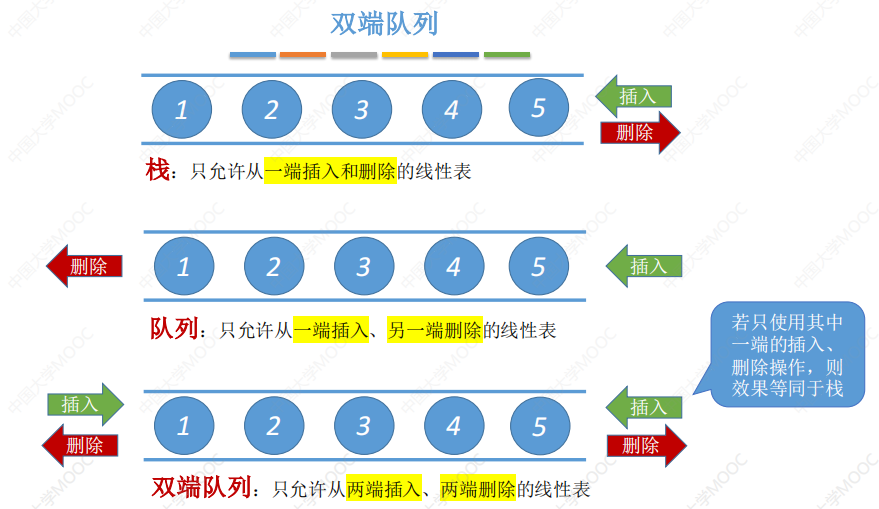
应用
括号匹配
用栈实现括号匹配:
依次扫描所有字符,遇到左括号入栈,遇到右括号则弹出栈顶元素检查是否匹配。
匹配失败情况:
- 左括号单身
- 右括号单身
- 左右括号不匹配
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ux1zXkJz-1686635230730)(null)]
//括号匹配
bool bracketCheck(char* str, int length) {
SqStack S;
InitStack(S);//初始化一个栈
for (int i = 0; i < length; i++) {
if (str[i] == '(' || str[i] == '[' || str[i] == '{') {
Push(S, str[i]);//扫描到左括号,入栈
}
else {
if (StackEmpty(S))return false;//扫描到右括号且当前栈空,匹配失败
char topElem;
Pop(S, topElem);//栈顶元素出栈进行匹配
if (str[i] == ')' && topElem != '(')
return false;
if (str[i] == ']' && topElem != '[')
return false;
if (str[i] == '}' && topElem != '{')
return false;
}
}
return StackEmpty(S);//最后检查栈,若空匹配成功,非空匹配失败
}
前中后缀表达式

中缀转后缀(左优先):
当中缀表达式转后缀表达式时,由于运算顺序的不同,可能存在转换为几种不同后缀表达式的情况,此时我们采用左优先原则,保证手算和机算的结果相同。
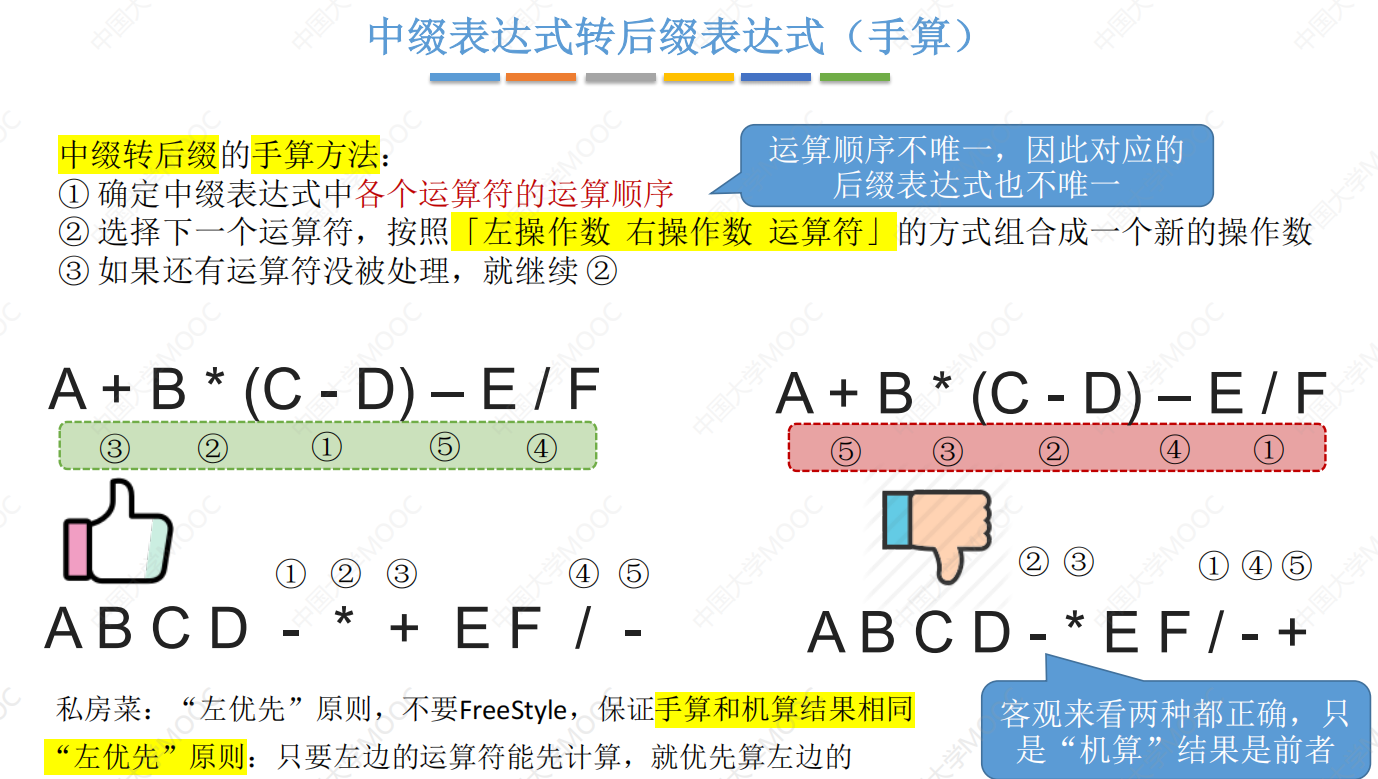
中缀转后缀的机算方法:

后缀表达式的手算方法:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-LQohQ0cw-1686635230708)(null)]
后缀表达式机算:利用栈 先弹出的元素为右操作数
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-hquCC1K8-1686635232135)(null)]
中缀转前缀(右优先):下图以右边的为准
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-GWXSUUrm-1686635230687)(null)]
前缀表达式机算:利用栈 先弹出的元素是左操作数

中缀表达式的计算(用栈实现)

栈在递归中的运用
适合用“递归”解决:可以把原始问题转换为属性相同,但规模较小的问题。

队列的运用
树的层次遍历
图的广度优先遍历
操作系统中FCFS先来先服务的策略
数组
数组的存储
一维数组:

二维数组(分为按行存储以及按列存储):


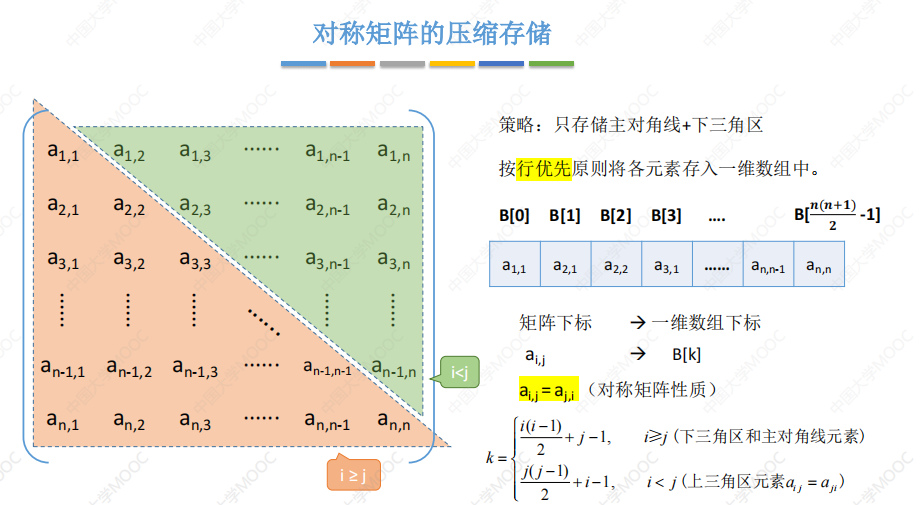
对称矩阵
若n阶方阵中任意一个元素aij都有aij=aji则该矩阵为对称矩阵。
同样分为行优先以及列优先
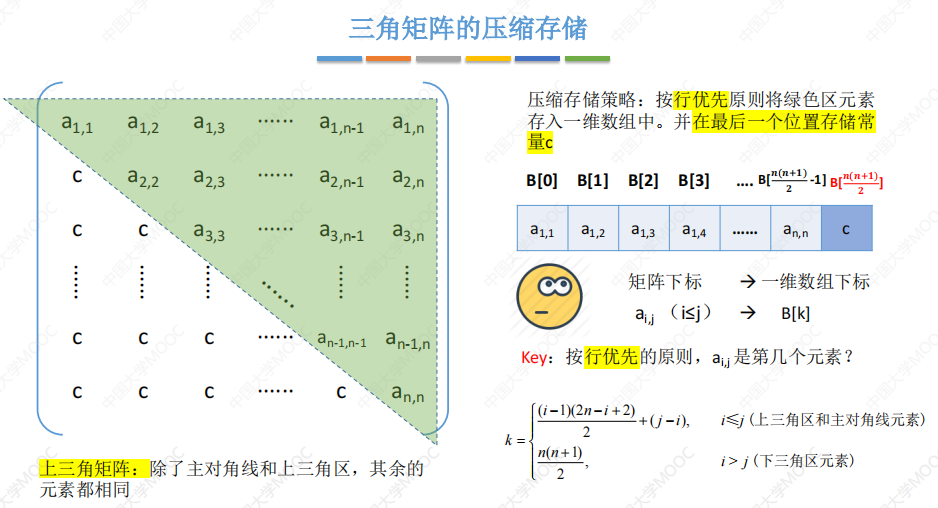
三角矩阵
下三角矩阵:除了主对角线和下三角区,其余的元素都相同。
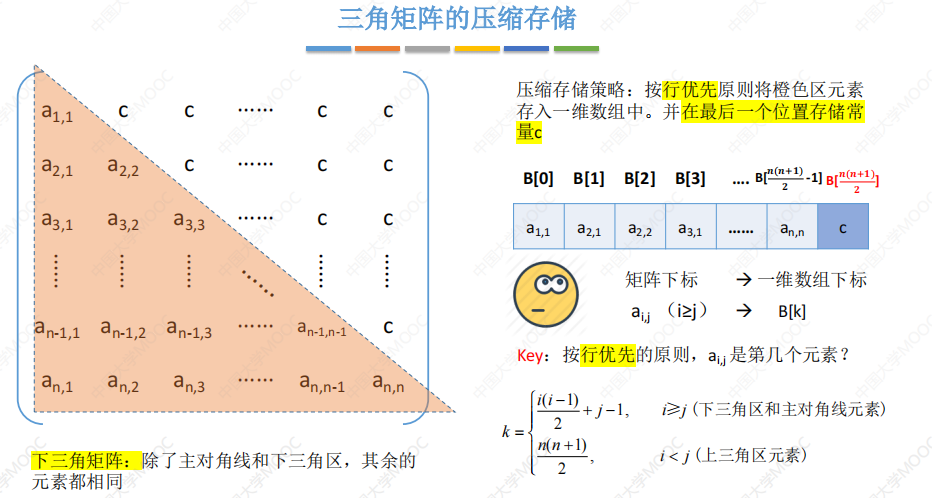
上三角矩阵:除了主对角线和上三角区,其余的元素都相同。
三对角矩阵
又称带状矩阵,当|i-j|>1时,有aij=0(1<=i,j<=n)
由i,j得到k:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-OrvwDtj5-1686635230798)(null)]
由k得到i,j:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-jVAIDTvc-1686635230774)(null)]
由k以及i的表达式可以进一步得到j的表达式
稀疏矩阵
非零元素远远少于矩阵元素的个数
使用三元组存储:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-HFGHxhSc-1686635230753)(null)]
使用十字链表法存储:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-xMbahDSY-1686635230660)(null)]
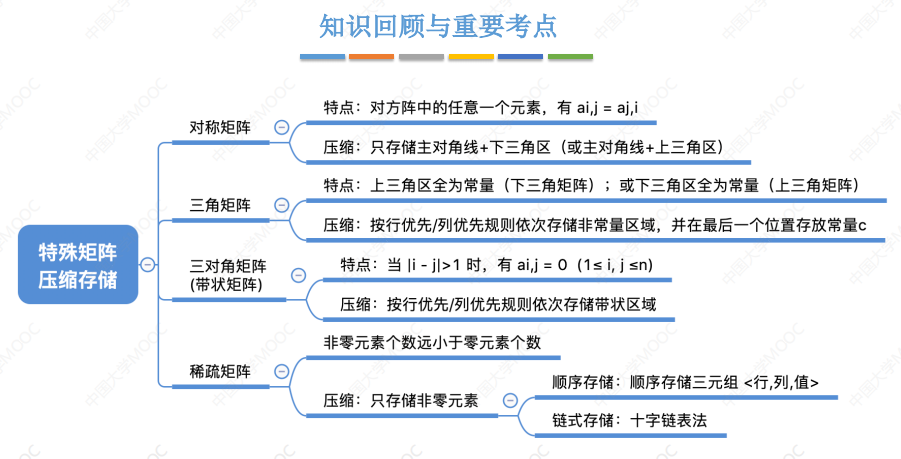
总结:
主要参考:王道考研课程
后续会持续更新考研408部分的学习笔记,欢迎关注。
github仓库(含所有相关源码):408数据结构笔记