线性代数
标量(scalar)
标量就是一个单独的数,只具有数值大小,而没有方向,部分有正负之分。一般用小写的变量名称表示,如a、x等。
向量(vector)
一个向量就是一列数,这些数是有序排列的。
可以把向量看作空间中的点,每个元素是不同坐标轴上的坐标。
当需要明确表示向量中的元素时,我们一般将元素排列成一个方括号包围的纵列:

向量在python中的实现如下:
a=np.array([1,2,4,3,8])
矩阵(matrix)
矩阵是一个二维数组,通常会赋予矩阵粗体的大写变量名称,比如 A。
矩阵在python中的实现如下:
A=np.array([[1,2,3],[4,5,6]])
张量(tensor)
一般的,一个数组的元素分布在若干维坐标的规则网格中,称之为张量。
可以将标量视为零阶张量,向量视为一阶张量,那么矩阵就是二阶张量,三阶就称为三阶张量
转置(transpose)
转置是矩阵的重要操作之一。矩阵的转置是以对角线为轴的镜像,这条从左上角到右下角的对角线被称为主对角线。定义如下:
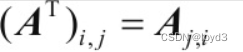
如:

矩阵乘法
为了使乘法可被定义,矩阵A的列数必须和矩阵 B的行数相等。如果矩阵A的形状是 m x n,矩阵B的形状是n x p,那C的形状是m x p。
特殊矩阵
单位矩阵
单位矩阵的结构很简单,就是所有沿主对角线上的元素都是1,而其他位置元素都是0的方阵(行数等于列数的矩阵)
可逆矩阵
矩阵的逆矩阵,矩阵和逆矩阵相乘得到单位举证
对角矩阵
对角矩阵只有在主对角线上才有非零元素,其余都是0。
下面这个就是对角矩阵

对称矩阵
对称矩阵,对于任意一个n阶方阵A,若A满足:A=AT成立,则称方阵A为对称矩阵。
范数(norm)
经常使用称为范数的数来衡量向量大小。范数是将向量映射到非负值的函数。直观上来说,向量x的范数衡量从原点到点x的距离。在某些机器学习应用中,区分恰好是零的元素和非零但值很小的元素是很重要的。
实际编程中如何计算向量的范数,看下面代码:
import numpy as np
import numpy.linalg as LA #导入Numpy中线性代数库
x=np.arange(0,1,0.1) #自动生成一个[0,1)间的10个数,步长为0.1
print(x)
x1= LA.norm(x,1) #计算1范数
x2= LA.norm(x,2) #计算2范数
xa=LA.norm(x,np.inf) #计算无穷范数
print(x1)
print(x2)
print(xa)
打印结果如下:
[ 0. 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9]
4.5
1.68819430161
0.9
最大范数(max norm)
这个范数表示向量中具有最大幅值的元素的绝对值
特征分解(cigendecomposition)
特征分解是使用最广的矩阵分解之一,即将矩阵分解成一组特征向量和特征值。
方阵A的特征向量是指与A相乘后当于对该向量进行缩放的非零量v:
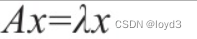
这里我们介绍了给定一个方阵时,如何求该方阵的特征向量和特征值,以及如何用编程语言实现。具体请看如下示例:
import numpy as np
a = np.array([[1,2],[3,4]]) # 示例矩阵
A1 = np.linalg.eigvals(a) # 得到特征值
A2, V1 = np.linalg.eig(a) # 其中A2也是特征值,B为特征向量
print(A1)
print(A2)
print(V1)
说明:
在numpy.linalg模块中:
eigvals():计算矩阵的特征值。
eig():返回包含特征值和对应特征向量的元组。
奇异值分解
一般矩阵的分解方法,称为奇异值分解,奇异值分解是将矩阵分解为奇异向量和奇异值。通过奇异值分解,会得到一些与特征分解相同类型的信息。然而,奇异值分解有更广泛的应用。每个实数矩阵都有一个奇异值分解,但不一定有特征分解。
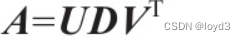
假设A是一个m×n矩阵,那么U是一个m×m矩阵,D是一个m×n矩阵,V是一个n×n矩阵。这些矩阵每一个都拥有特殊的结构,其中U和V都是正交矩阵,D是对角矩阵(注意,D不一定是方阵)。对角矩阵D对角线上的元素被称为矩阵A的奇异值。矩阵U的列向量被称为左奇异向量,矩阵V的列向量被称右奇异向量。
SVD最有用的一个性质可能是拓展矩阵求逆到非方矩阵上。
用Python的实现如下:
import numpy as np
Data=np.mat([[1,1,1,0,0],
[2,2,2,0,0],
[3,3,3,0,0],
[5,5,3,2,2],
[0,0,0,3,3],
[0,0,0,6,6]])
u,sigma,vt = np.linalg.svd(Data)
print(sigma)
#转换为对角矩阵
diagv=np.mat([[sigma[0],0,0],[0,sigma[1],0],[0,0,sigma[2]]])
print(diagv)
结果如下:
[ 1.09824632e+01 8.79229347e+00 1.03974857e+00 1.18321522e-15
2.13044868e-32]
[[ 10.98246322 0. 0. ]
[ 0. 8.79229347 0. ]
[ 0. 0. 1.03974857]]
迹运算
迹运算返回的是矩阵对角元素的和:
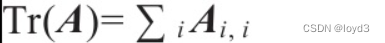
迹运算在某些场合非常有用。若不使用求和符号,有些矩阵运算很难描述,而通过矩阵乘法和迹运算符号可以清楚地表示。
利用Python的NumPy对矩阵求迹
C = np.array([[1,2,3],[4,5,6],[7,8,9]])
TrC = np.trace(C)
D=C-2
TrCT = np.trace(C.T)
TrCD = np.trace(np.dot(C,D))
TrDC = np.trace(np.dot(D,C))
print(TrC)
print(TrCT)
print(TrCD)
print(TrDC)
打印结果
15
15
171
171
用Python实现主成分分析
主成分分析(Principal Component Analysis,PCA)是一种统计方法。通过正交变换将一组可能存在相关性的变量转换为一组线性不相关的变量,转换后的这组变量叫主成分。
可以参考:https://blog.csdn.net/wyn1564464568/article/details/125898241