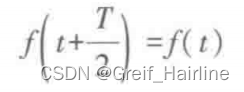连续信号的正交分解
- 3.1引言
- 3.3信号表示为傅里叶级数(FS)
- 三角傅里叶级数
- 1. 本质
- 展开式1
- 展开式2
- 展开条件-狄利克雷条件
- 分量概念
- 补充
- 指数傅里叶级数
- 使用条件
- 形式1(按连续信号的正交分解定义展开)
- 形式2(由三角函数形式的傅里叶级数推导)
- 各展开式的联系
- 注意事项
- 函数的奇偶性质与谐波含量的关系
- 1.奇偶函数
- 2. 奇谐函数
- 3. 偶谐函数
3.1引言
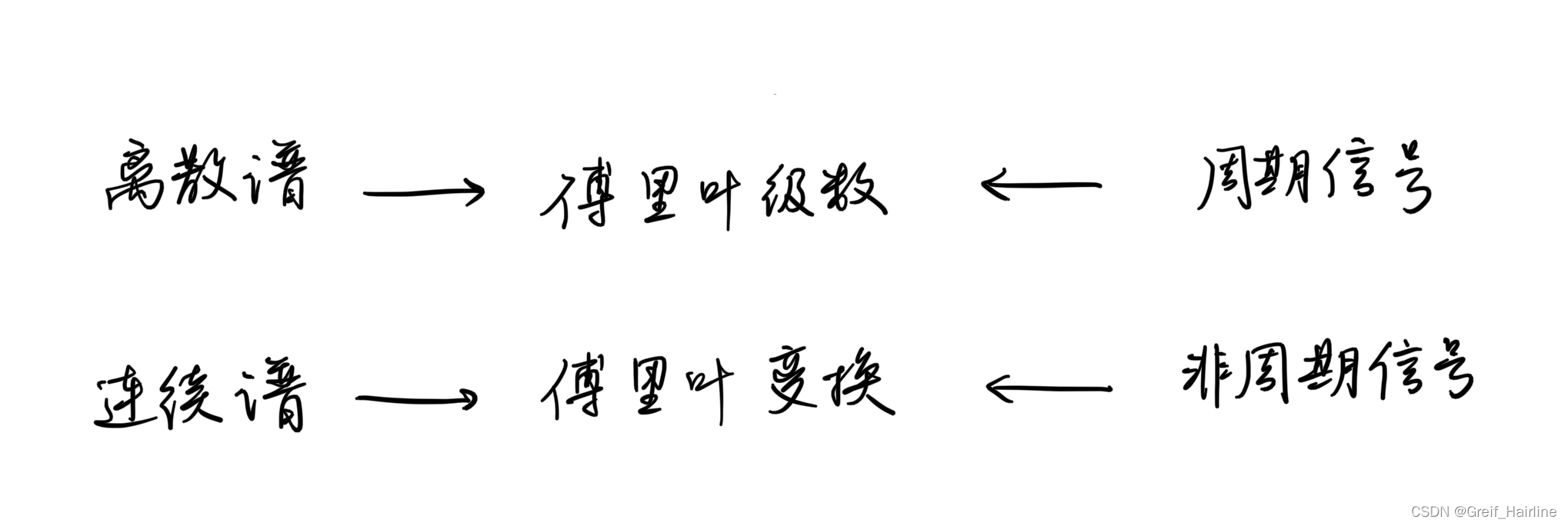
时域中,近代时域法将信号分解为冲激信号的和,根据冲激响应与激励信号的卷积计算系统对信号的响应;频域中,将信号分解为一系列正弦信号的和,通过系统对正弦信号的响应求解系统对信号的响应
3.3信号表示为傅里叶级数(FS)
三角傅里叶级数
1. 本质
将任意信号在正交函数集(三角函数是最常用的正交函数集)中展开,即表示成该正交集函数的线性组合
展开式1
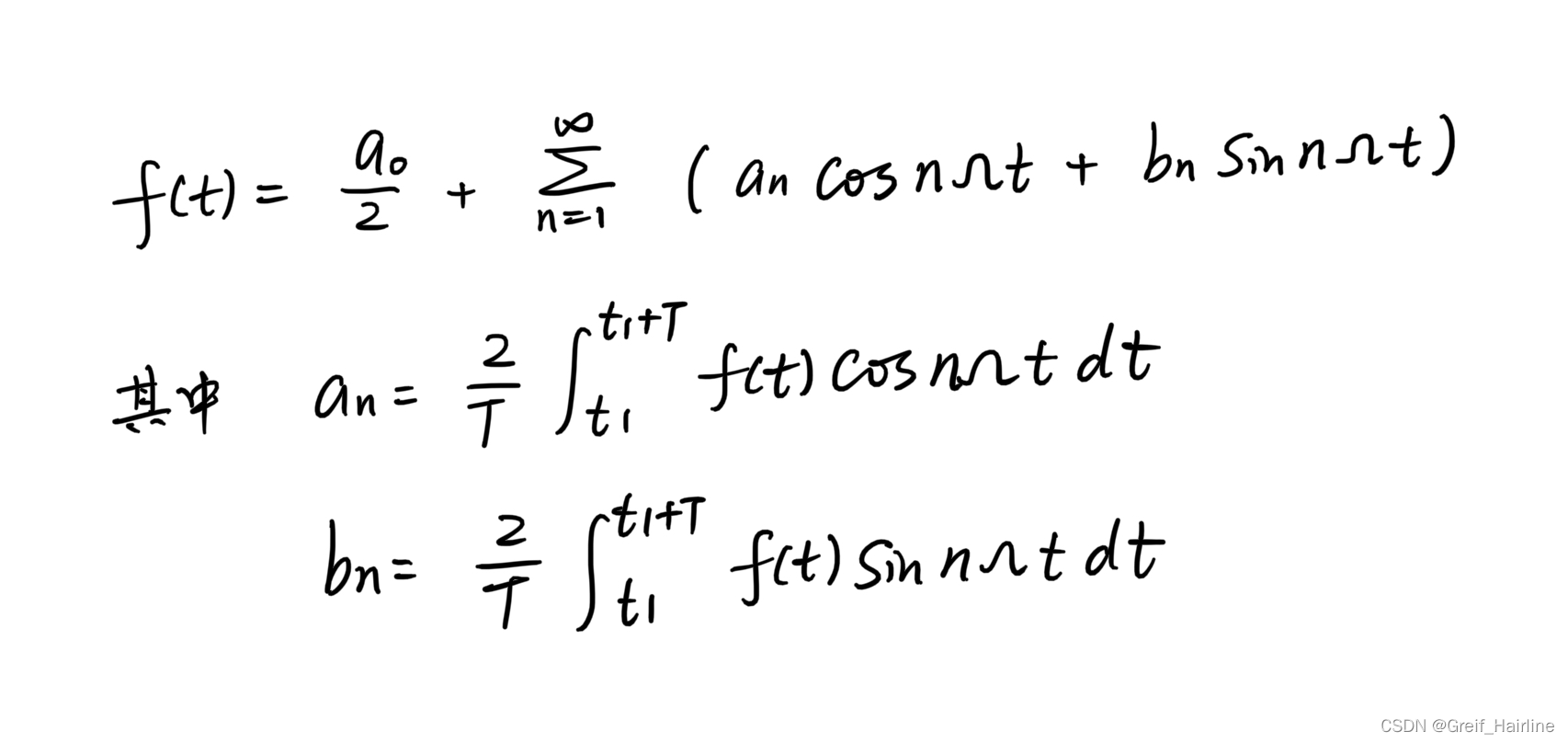
展开式2
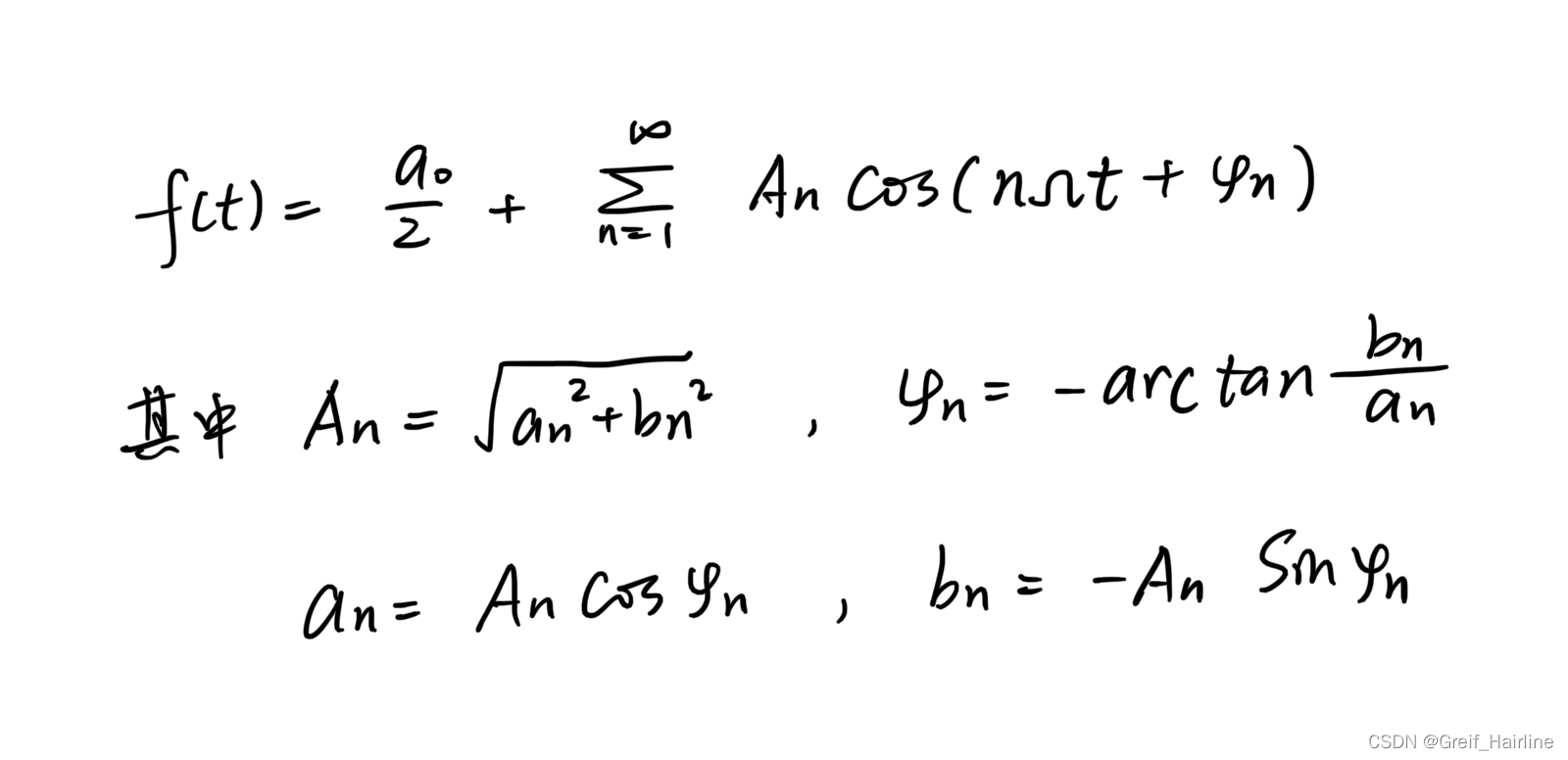
展开条件-狄利克雷条件
本质: 等式左右两边的函数的差的方均误差趋于零
条件:
在一个周期内,函数绝对可积
在一个周期内,函数的极值数有限
在一个周期内,函数连续或有有限个间断点
分量概念
直流分量
基波分量
n次谐波分量
补充

指数傅里叶级数
使用条件
当方波占空比比较小,而且不具有奇偶性时,宜用指数形式
形式1(按连续信号的正交分解定义展开)
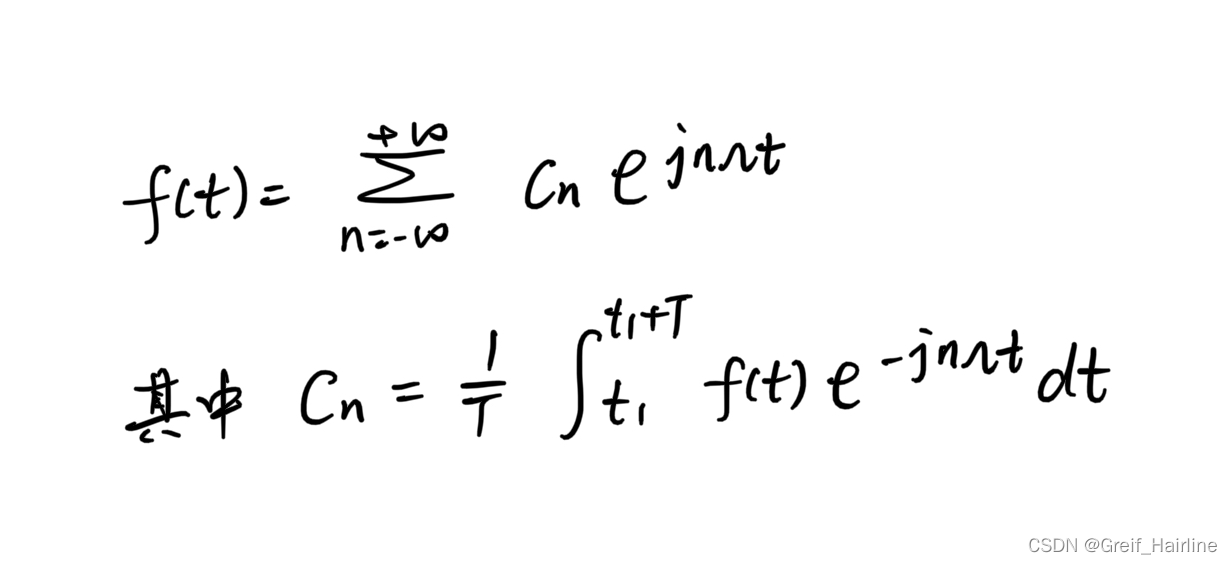
形式2(由三角函数形式的傅里叶级数推导)
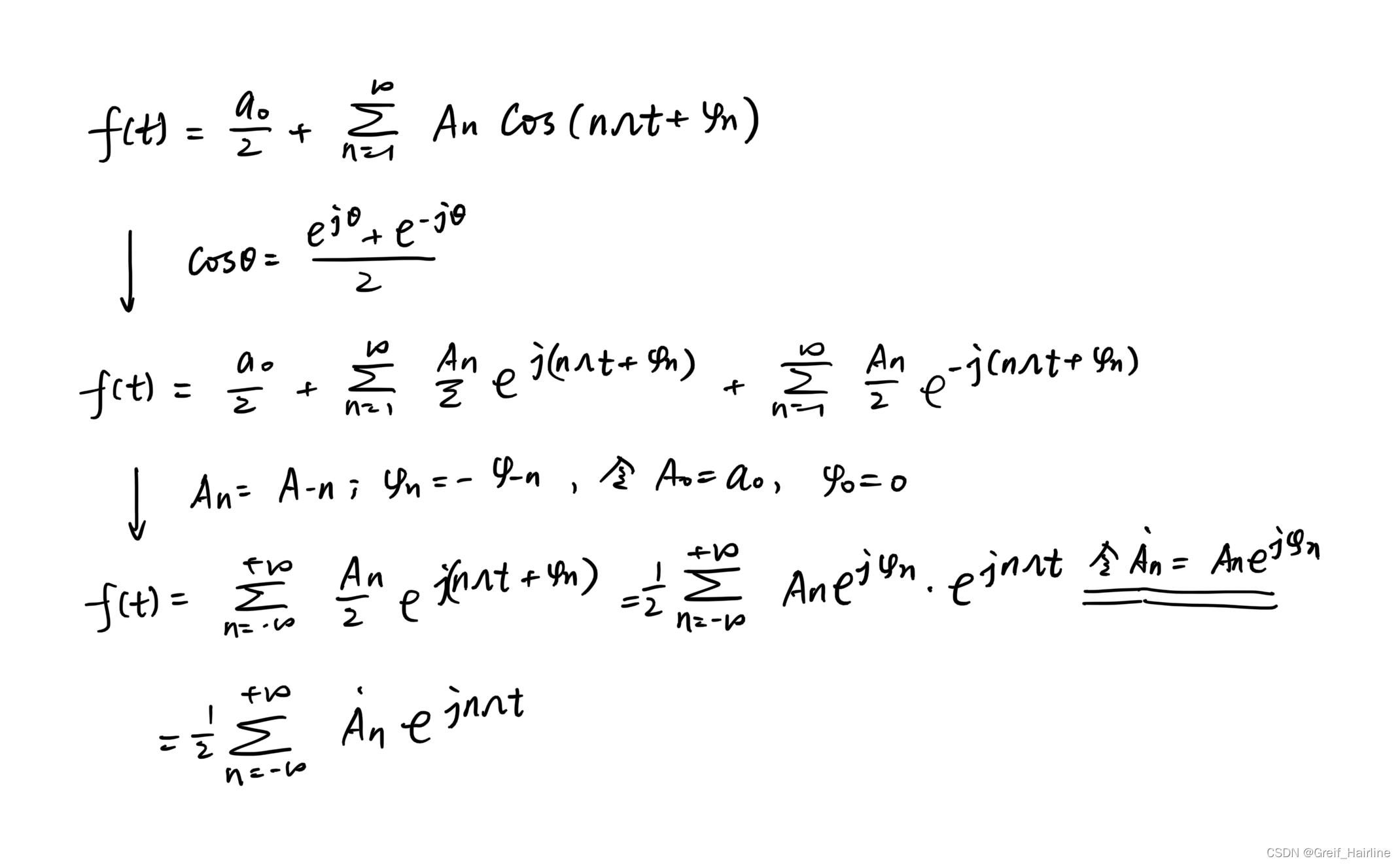
各展开式的联系

注意事项
arctan计算时,要考虑an和bn的象限,一四象限不变,第二象限+π,第三象限-π
函数的奇偶性质与谐波含量的关系
1.奇偶函数
奇函数的傅里叶级数中只有正弦分量
偶函数的傅里叶级数中只有直流和余弦分量
2. 奇谐函数
定义
性质: 奇谐函数的傅里叶级数中只有奇次谐波分量
3. 偶谐函数
定义
性质: 偶谐函数的傅里叶级数只有直流和偶次谐波分量