文章目录
- 1.递归函数的概念
- 2.递归函数的使用
- 2.1.案例一
- 2.1.1.需求描述
- 2.1.2.使用常规的循环来实现
- 2.1.3.使用递归函数实现
- 2.2.案例二
- 2.2.1.需求描述
- 2.2.2.使用常规的循环来实现
- 2.2.3.使用递归函数实现
- 3.使用递归函数计算阶乘
- 3.1.阶乘的概念
- 3.2.使用递归函数实现阶乘的算法
- 3.3.以常规循环实现阶乘算法
- 4.使用递归函数计算斐波那契数列
1.递归函数的概念
在一个函数体内,可以调用其他函数,如果在函数体内调用了该函数本身,这个函数就称为递归函数。
例如我们定义了一个fun函数,如果在fun函数体中又调用了fun函数,这就是递归函数。
递归函数包含了隐式的循环,会不停的将函数本身反复的执行,因此递归函数必须有一个明确的递归结束条件,也称为递归出口。
当没有明确的递归结束调节时,递归函数是在函数体中不停的重复调用自身函数的无限循环,就可能造成内存溢出的情况,谨慎使用,毕竟使用循环去解决问题不是稳妥的方案。
递归函数可以认为是一个死循环,会无限循环的执行函数体中的代码,因此我们必须要有一个明确的递归结束条件,否则将一直处于死循环体内,最终导致内存溢出。
使用递归函数来解决的问题必须满足两个条件:
- 可以通过递归调用来缩小问题的规模,且新问题与原问题有相同的形式。
- 例如我们本来要计算n的结果,但是使用递归后就可以计算n-1的结果,缩小了问题的规模
- 可以存在一种简单的情境,可以使递归在简单情境下退出。
递归函数的优点在于定义简单,逻辑清晰。
递归最核心的思想是:每一次递归,整体问题都要比原来减小,并且递归到一定层次时,要能直接给出结果!
使用递归函数需要注意防止递归深度溢出,在Python中,通常情况下,这个深度是1000层,超过将抛出异常。在计算机中,函数递归调用是通过栈(stack)这种数据结构实现的,每当进入一个递归时,栈就会加一层,每当函数返回一次,栈就会减一层。由于栈的大小不是无限的,所以,递归调用的次数过多,会导致栈溢出。
递归遍历结束后,会将每次递归的结果进行回归,例如下图是一个阶乘的递归函数用法,递推函数是n * fac(n-1),每次递归求出fac(x),如下图每次递归得到fac(6)、fac(5)、fac(4)、fac(3)、fac(2)、fac(1),最后还需要依次回归得到6 * ( 5 * ( 4 * ( 3 * ( 2 * fac(1)))))。
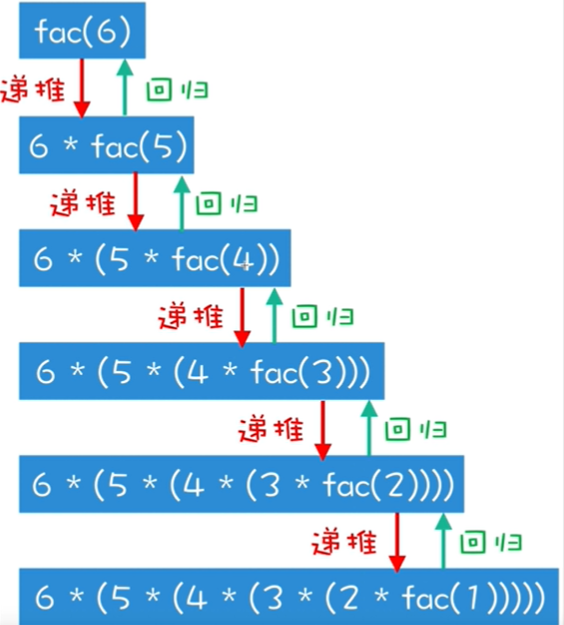
递归最核心的点就在于递推+回归,首先递推循环出所有可遍历的表达式,最后一次递推符合结束条件了,取到return返回值,然后使用最后一个递推得到的return返回值,依次与前一个递推进行回归,得到最终的结果。
2.递归函数的使用
2.1.案例一
2.1.1.需求描述
需求:
- 1)调用函数时可以传入任意的字符串。
- 2)判断传入的字符串长度是否小于5,如果小于5,则拼接一组字符串,这个字符串由(传入的实参+‘h’)组成。
- 3)且拼接的字符串也要去判断长度是否小于5,如果小于5,则为其拼接一个’h’字符,通过循环的手段,直到拼接的字符串长度为4时为止,每次循环判断时,字符串要求是上次循环的结果。
- 4)最后与传入的实参进行拼接,拼接时要将每次循环的结果都与实参进行拼接。
- 5)如果一开始传入的字符串长度就大于5,则直接返回。
例如,我传入一个ha字符串,最后要给我返回出hahahhahhhahhh。
其中ha是传入的实参,hahhahhhahhh是拼接字符串,拼接字符串第一次循环判断,长度为2,小于5,那么就拼接一个h字符,得到结果为hah,第二次循环的长度为3,小于5,那么就拼接一个h字符,得到结果为hahh,第三次循环的长度为4,小于5,那么就拼接一个h字符,得到结果hahhh,第四次循环不小于5了,循环结束,将每次循环的结果都拼接在一起,最后再和传入的实参拼接,得到hahahhahhhahhh。
2.1.2.使用常规的循环来实现
实现思路:
- 首先定义一个外层循环,判断传入的实参长度是否小于5,如果小于5,则为其拼接字符串,否则将直接返回实参值
- 由于拼接的字符串很有特点,拼接的字符串由传入的实参+h字符组成,因此将传入的实参赋值给另外一个变量para2,后续好拼接。
- 还需要判断拼接的字符串长度是否小于5,因此我们还要再声明一个内层循环,变量para2就是拼接的字符串,判断拼接的字符串是否小于5,如果小于5,则将para2的变量值与字符h进行拼接,然后再赋值给para2变量,这样一来,本次循环拼接的结果就定义在变量para2中了,下次循环也会按照上次循环的结果进行判断。
- 将拼接的结果定义在para2变量中,还可以与传入的实参进行拼接,将para2变量与形参para1进行拼接,从而使得每次循环后,将得到的结果都与传递的实参进行一次拼接。
def join_5_str(para1):
#首先定义一个循环,判断实参长度是否小于5,如果小于5,则进入循环
while len(para1) < 5:
#将形参para1的实参赋值给para2变量,拼接的字符串格式由传入的实参+'h'字符组成,因此可以将传入的实参先放在另外一个变量para2中
para2 = para1
#判断para2变量值的长度是否小于5,如果小于5,则进入循环
while len(para2) < 5:
#拼接字符串,将para2的变量值与字符'h'进行拼接,然后再赋值给para2变量
para2 = para2 + 'h'
#完成最终的字符串拼接,每次循环都会进行拼接,相当于是将每次的循环结果都进行了拼接
#para1的变量值是传入的实参,para2的值是本次循环的拼接结果,然后将para1和para2拼接在一起,赋值给para1变量
para1 = para1 + para2
#如果实参的长度大于五,返回实参的值
else:
return para1
调用函数传入ha字符串,观察返回值。
print(join_5_str('ha'))
#输出结果:hahahhahhhahhh

函数的执行过程分析如下:
- 传入实参’ha’给形参para1,首先判断ha的长度是否小于5,如果小于5,则进入第一次外层循环,最外侧的循环只会循环一次,因为内层子循环完毕后,字符串的长度一定大于5。
- 将ha赋值给para2变量,然后再判断para2拼接字符串的长度是否小于5,如果小于5,则开始第一次内层循环:
- 开始第一次内层循环,para2的值为ha,长度为2,小于5,条件成立,将ha与h进行拼接,得到hah,然后再赋值给para2变量,再将hah与传入的实参ha进行拼接得到hahah,再赋值给para1变量。
- 第一次内层循环时会将结果再次赋值给para2变量,因此开始第二次循内层环时,para2的值为hah,para2的长度为3,长度小于5,为hah拼接一个h,得到hahh,然后再赋值给para2变量,再将hahh与para1变量进行拼接,再赋值给para1变量,此时就会得到hahahhahh。
- 开始第三次内层循环,思路也一样,para2的值为hahh,para2的长度为4,小于5,为hahh拼接一个h,得到hahhh,然后赋值给para2变量,再将hahhh与para1变量进行拼接,此时就会得到此时就会得到hahahhahhhahhh。
- 第四次开始内层循环,此时para2的值为hahhh,长度大于5,循环结束。
- 然后开始第二次外层循环,para1的值此时为hahahhahhhahhh,长度大于5,直接返回。
2.1.3.使用递归函数实现
我们的需求很有特色,你判断传入的字符串是否小于5,小于5就给拼接字符串,那你直接拼接不就好了吗,拼接的字符串来源于传入的实参,如果拼接的字符串也小于5,那么同样要进入循环判断,然后拼接一个字符h,这样一来我们就用了两次循环,如果需求更加恶心一点,要对拼接中的拼接中的拼接中的字符串长度进行判断,都要小于5,那我们岂不是要写很多循环体了。
为了避免写如下一大堆的while循环,建议大家基于这种情况去使用递归函数来实现。
#运用递归函数
def join_5_str(para1):
#判断实参的长度是否小于5,这也是递归函数的结束条件,只要不小于5了,递归循环就会结束
if len(para1) < 5:
#那么就为其拼接字符串,para1实参+递归函数join_5_str(para1 + 'h')的结果
return para1 + join_5_str(para1 + 'h')
else:
return para1
#调用函数传入字符串ha
print(join_5_str('ha'))
#输出结果:hahahhahhhahhh
'''
return para1 + join_5_str(para1 + 'h')代码解释:
在这行代码中调用了join_5_str自身函数,相当于使用递归函数了,递归函数是一个隐式的循环体。
join_5_str(para1 + 'h')是递归函数的本体,递归函数的特点就是隐式循环,使用自身函数test2去处理(para1 + 'h'),第一次循环para1的值为调用join_5_str函数时传递的位置实参ha,每次都会将循环后的结果赋值给递归函数中的para1形参,依次循环,直到if len(para1) < 5条件不满足时结束递归函数的循环,拿到递归函数的返回结果,最后和函数体中的para1进行拼接。
para1 + 'h'相当于para1 = para1 + 'h'。
递归函数的循环过程;
1)递归函数第一次循环:para1形参的值为ha,与h拼接后得到:para1 = ha + h,结果为hah,字符串的长度为3,满足if len(para1) < 5条件,继续进入下一次循环。
2)递归函数第二次循环:para1形参的值为上次循环的结果为hah,与h拼接后得到:para1 = hah + h,结果为hahh,字符串的长度为4,满足if len(para1) < 5条件,继续进入下一次循环。
3)递归函数第三次循环:para1形参的值为上次循环的结果为hahh,与h拼接后得到:para1 = hahh +h,结果为hahhh,字符串的长度为5,此时就不满足if len(para1) < 5这个条件了,递归函数循环结束。
由于递归函数前的运算符是加法+,因此递归函数循环结束后,会将每次循环的结果相加,循环结果返回的如果是字符串就相当于字符串拼接,如果是数字就会累加求和,最终递归函数的结果就是:hah+hahh+hahhh=hahhahhhahhh。
此时函数体中的para1的值就会和递归函数进行拼接,ha+hahhahhhahhh,得到hahahhahhhahhh。
如果一开始para1形参接收的实参字符长度超过5了,就不会再使用递归函数拼接其他字符串,从而直接返回原字符串。
'''
上述的解释是一种特别通俗易懂的解释,不是很明白递归原理的可以先看上面的解释,当熟悉递归函数后我们也可以用递归函数的递推+回归的方式去解释:
1)首先开始递推:
- 调用函数时传入para1的实参为ha
- 开始第一次递推:ha + h
- 开始第二次递推:ha + h + h
- 开始第三次递推:ha + h +h +h,此时不符合递归条件了,结束循环。
2)开始回归:
- 从最后一次递推的值依次向上回归。
- 第一次回归(第二次递推的值)hahh+(第三次回归的值)hahhh
- 第二次回归(第一次递推的值)hah+(第二次回归的值)hahhhahhh
- 调用函数时传的实参ha+递归函数的返回值hahhhahhh,得到hahahhahhhahhh
2.2.案例二
和案例一很类似,只不过将字符串换成了数字,只为演示:递归函数循环结束后,会将每次循环的结果相加,循环结果返回的如果是字符串就相当于字符串拼接,如果是数字就会累加求和。
2.2.1.需求描述
需求:
- 1)调用函数时可以传入任意的数字。
- 2)判断传入的数字是否小于5,如果小于5,则加上一个数字,这个数字由(传入的实参 + 1)组成
- 3)且加的这个数字也要去判断是否小于5,如果小于5,则为其加1,通过循环的手段,直到加的这个数字为4时为止,每次循环判断时,数字要求是上次循环的结果。
- 4)最后与传入的实参进行相加,相加时要将每次循环的结果都与实参进行相加。
- 5)如果一开始传入的数字实参就大于5,则直接返回。
例如,我传入一个数字1,最后返回的结果就是15。
其中1是传入的实参,14是最后返回的结果,要为实参加的数字第一次循环判断,数字为1,小于5,那么就为其加1,得到结果为1+1=2,第二次循环的数字为2,小于5,那么就为其加1,得到结果为2+1=3,第三次循环的数字为3,小于5,那么就为其加1,得到结果3+1=4,第四次循环的数字为4,小于5,那么就为其加1,得到的结果4+1=5,第五次循环的数字为5,不小于5了,循环结束,将每次循环的结果都相加在一起2+3+4+5,最后再和传入的实参相加1+2+3+4+5,得到15。
2.2.2.使用常规的循环来实现
实现思路:
- 首先定义一个外层循环,判断传入的实参是否小于5,如果小于5,则为其加一个数字,否则将直接返回实参值。
- 由于拼接的数字很有特点,拼接的数字由传入的实参+1组成,因此将传入的实参赋值给另外一个变量para2,后续好相加。
- 还需要判断拼接的数字是否小于5,因此我们还要再声明一个内层循环,变量para2就是相加的数字,判断拼接的数字是否小于5,如果小于5,则将para2的变量值与1进行相加,然后再赋值给para2变量,这样一来,本次循环相加的结果就定义在变量para2中了,下次循环也会按照上次循环的结果进行判断。
- 将相加的结果定义在para2变量中,还可以与传入的实参进行相加,将para2变量与形参para1进行相加,从而使得每次循环后,将得到的结果都与传递的实参进行一次相加。
def sum_5_int(para1):
#首先定义一个循环,判断实参是否小于5,如果小于5,则进入循环
while para1 < 5:
#将形参para1的实参赋值给para2变量,相加的数字格式由传入的实参 + 1组成,因此可以将传入的实参先放在另外一个变量para2中
para2 = para1
#判断para2变量值的是否小于5,如果小于5,则进入循环
while para2 < 5:
#相加数字,将para2的变量值与1进行相加,然后再赋值给para2变量
para2 = para2 + 1
#完成最终的数字相加,每次循环都会进行相加,相当于是将每次的循环结果都进行了相加
#para1的变量值是传入的实参,para2的值是本次循环的相加结果,然后将para1和para2相加,赋值给para1变量
para1 = para1 + para2
else:
return para1
传入一个数字1,观察返回值。
print(sum_5_int(1))
#输出结果:15

函数的执行过程分析如下:
- 传入实参1给形参para1,首先判断1的是否小于5,如果小于5,则进入第一次外层循环,最外侧的循环只会循环一次,因为内层子循环完毕后,数字一定大于5。
- 将1赋值给para2变量,然后再判断para2相加的数字是否小于5,如果小于5,则开始第一次内层循环:
- 开始第一次内层循环,para2的值为1,小于5,条件成立,将1与1进行相加,得到1+1=2,然后再赋值给para2变量,再将2与传入的实参1进行拼接得到3,再赋值给para1变量。
- 第一次内层循环时会将结果再次赋值给para2变量,因此开始第二次循内层环时,para2的值2,小于5,为2加1,得到2+1=3,然后再赋值给para2变量,再将3与para1变量进行相加,再赋值给para1变量,此时就会得到6。
- 开始第三次内层循环,思路也一样,para2的值为3,小于5,为3加1,得到3+1=4,然后赋值给para2变量,再将3与para1变量进行相加,此时就会得到10。
- 第四次开始内层循环,para2的值为4,小于5,为4加1,等到4+1=5,然后赋值给para2变量,再将5与para1变量进行相加,此时就会得到15。
- 第五次开始内层循环,para2的值为5,不小于5,循环结束。
- 然后开始第二次外层循环,para1的值此时为15,长度大于5,直接返回。
2.2.3.使用递归函数实现
def sum_5_int(para1):
#判断实参的是否小于5,这也是递归函数的结束条件,只要不小于5了,递归循环就会结束
if para1 < 5:
#那么就为其相加一个数字,para1实参+递归函数sum_5_int(para1 + 1)的结果
return para1 + sum_5_int(para1 + 1)
#sum_5_int(para1 + 1)递归函数的循环结果依次为:(1+1)+(2+1)+(3+1)+(4+1)
else:
return para1
print(sum_5_int(1))
'''
return para1 + sum_5_int(para1 + 1)代码解释:
在这行代码中调用了sum_5_int自身函数,相当于使用递归函数了,递归函数是一个隐式的循环体。
sum_5_int(para1 + 1)是递归函数的本体,递归函数的特点就是隐式循环,使用自身函数sum_5_int去处理(para1 + 1),第一次循环para1的值为调用sum_5_int函数时传递的位置实参1,每次都会将循环后的结果赋值给递归函数中的para1形参,依次循环,直到if para1 < 5条件不满足时结束递归函数的循环,拿到递归函数的返回结果,递归函数每次循环的结果都会累加在一起,最后和函数体中的para1进行相加,并返回。
para1 + 1相当于para1 = para1 + 1。
递归函数的循环过程;
1)递归函数第一次循环:para1形参的值为1,与1相加后得到:para1 = 1 + 1,结果为1+1=2,数字为2,满足if len(para1) < 5条件,继续进入下一次循环。
2)递归函数第二次循环:para1形参的值为上次循环的结果为2,与1相加后得到:para1 = 2 + 1,结果为2+1=3,数字为3,满足if len(para1) < 5条件,继续进入下一次循环。
3)递归函数第三次循环:para1形参的值为上次循环的结果为3,与1相加后得到:para1 = 3 + 1,结果为3+1=4,数字为4,满足if len(para1) < 5条件,继续进入下一次循环。
4)递归函数第四次循环:para1形参的值为上次循环的结果为4,与1相加后得到:para1 = 4 + 1,结果为4+1=5,数字为5,此时就不满足if len(para1) < 5这个条件了,此时递归函数循环结束。
由于递归函数前的运算符是加法+,因此递归函数循环结束后,会将每次循环的结果相加,循环结果返回的如果是字符串就相当于字符串拼接,如果是数字就会累加求和,最终递归函数的结果就是:1+(1+1)+(2+1)+(3+1)+(4+1)=15
如果一开始para1形参接收的实参字符长度超过5了,就不会再使用递归函数拼接其他字符串,从而直接返回原字符串。
'''
上述的解释是一种特别通俗易懂的解释,我们也可以用递归函数的递推+回归的方式去解释:
1)首先开始递推:
- 调用函数时传入para1的实参为1
- 开始第一次递推:1 + 1 = 2
- 开始第二次递推:2 + 1 = 3
- 开始第三次递推:3 + 1 = 4
- 开始第四次递推:4 + 1 = 5,此时不符合递归条件了,结束循环。
2)开始回归:
- 从最后一次递推的值依次向上回归。
- 第一次回归(第三次递推的值)4+(第四次回归的值)5 = 9
- 第二次回归(第二次递推的值)3 +(第三次回归的值)9 = 12
- 第三次回归(第一次递推的值)2 + (第二次回归的值)12 = 14
- 调用函数时传的实参1+递归函数的返回值14,得到15。
3.使用递归函数计算阶乘
3.1.阶乘的概念
正整数阶乘是数学中的一种概念,也是做开发者必须要知道的数学理念。
阶乘指的是所有小于该数的正整数的积,例如我们要求正整数2的阶乘,2的阶乘就是所有小于2的正整数的积,2! = 1 * 2 = 2。或者采用递归的方式,(2-1)*2=2,结果一样。
因此阶乘的公式就是:n! = 1 * 2 * 3 * 4 * ··· * n
递归阶乘的公式为:(n-1)! * n或者是n * (n -1)!
求6的阶乘:
普通阶乘的运算:
6! = 1 * 2 * 3 * 4 * 5 *6
= 720
递归阶乘的运算:
6! = (6-1)! * 6
相当于用5的阶乘去乘以6
递归阶乘和普通阶乘的运算结果一样,只不过递归阶乘能够缩小乘积的范围,运算出来的结果也是阶乘。
0的阶乘为0,1的阶乘为1。
3.2.使用递归函数实现阶乘的算法
下面我们来定义一个递归函数来实现阶乘的算法。
def factorial(num):
#0和1的阶乘都是本身,因此可以作为递归函数的循环结束条件
if num == 1:
return 1
#采用递归阶乘的算法来实现需求:n * (n -1)!
#定义阶乘的算法,传入的num形参值就是阶乘公式中的n,factorial(num - 1)就是(n -1)!
#factorial(num - 1)是递归函数,会循环执行factorial函数体,直到不满足条件位置,循环结束,也就相当于是(n -1)!阶乘的运算过程
return num * factorial(num - 1)
'''
代码解释:
首先定义一个递归函数的循环结束体,当num的变量值等于1时,结束循环,返回1。
如果不满足if num == 1条件,则执行num * factorial(num - 1)代码,计算传入的实参的阶乘。
计算实参的阶乘我们通过公式n * (n -1)!作为依据,例如传入2,得到的式子就是2*(2-1)! = 2*1! = 2
其中:n通过num形参传入,(n -1)!是计算阶乘的部分,所以通过递归函数循环去计算,然后将每次循环的结果累加在一起,最终就是传入实参的阶乘值。
'''
接下来调用factorial函数计算某个正整数的阶乘。
print(factorial(6))
print(factorial(600))

以传入实参6位里,我们来推理函数的运行过程:
- 1)首先判断实参6是否等于1,如果等于1则返回1,不再执行下面的代码。
- 2)如果实参6不等于1,那么进入阶乘的算法num * factorial(num - 1),num为6,factorial(num - 1)为递归函数,递归函数需要循环去运行本函数体中的代码,直到条件不满足后,将每次循环的结果都与num进行相乘,最后得到num的阶乘。
- 3)factorial(num - 1)递归函数循环过程:
- 1、第一次递归函数的循环:num形参为6,减1之后得到num = 6 - 1,结果为6-1=5,num为5,不满足if num == 1条件,进入下一次循环。
- 2、第二次递归函数的循环:num形参为5,减1之后得到num = 5 - 1,结果为5-1=4,num为4,不满足if num == 1条件,进入下一次循环。
- 3、第三次递归函数的循环:num形参为4,减1之后得到num = 4 - 1,结果为4-1=4,num为3,不满足if num == 1条件,进入下一次循环。
- 4、第四次递归函数的循环:num形参为3,减1之后得到num = 3 - 1,结果为3-1=2,num为2,不满足if num == 1条件,进入下一次循环。
- 5、第三次递归函数的循环:num形参为2,减1之后得到num = 2 - 1,结果为2-1=1,num为1,满足if num == 1条件,递归函数循环结束。
- 4)由于递归函数前的运算符是乘法
*,因此递归函数循环结束后,会将每次循环的结果相乘,最终递归函数的结果就是5*4*3*2*1。 - 5)最后再与传入的实参6进行相乘
6*5*4*3*2*1=720,那么实参6的阶乘就是720。
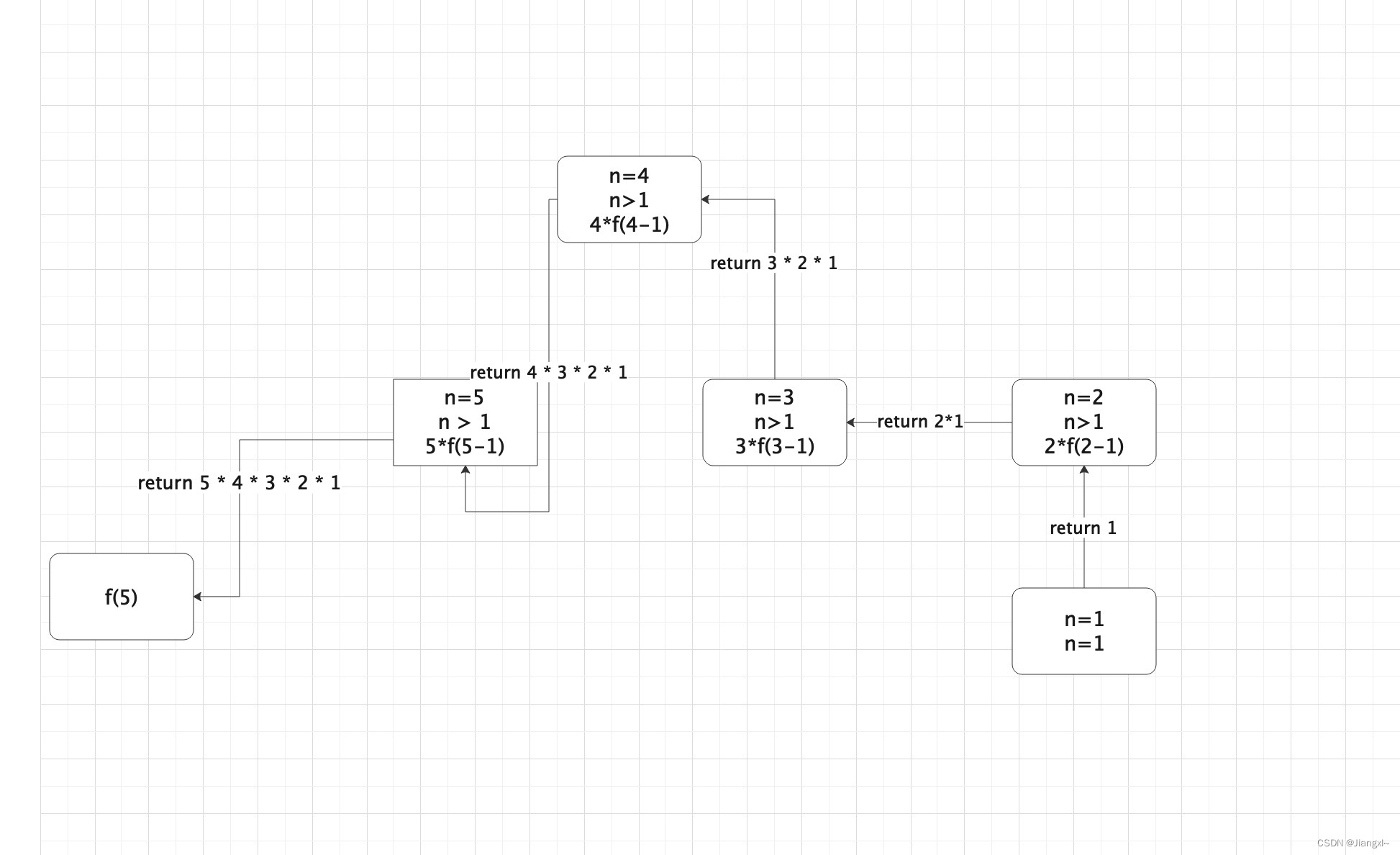
上述的解释是一种特别通俗易懂的解释,我们也可以用递归函数的递推+回归的方式去解释:
1)首先开始递推:
- 调用函数时传入para1的实参为6
- 开始第一次递推:factorial(6 - 1) = factorial(5)
- 开始第二次递推:factorial(5 - 1) = factorial(4)
- 开始第三次递推:factorial(4 - 1) = factorial(3)
- 开始第四次递推:factorial(3 - 1) = factorial(2)
- 开始第五次递推:factorial(2 - 1) = factorial(1),此时不符合递归条件了,结束循环。
2)开始回归:
- 最后一次递推得到的return返回值为1,从最后一次递推的值依次向上回归,本次递归使用的运算符是乘,因此回归的时候也是乘法。
- 第一次回归:(第五次递推的值)1 * (return返回值)1 = 1
- 第二次回归:(第四次递推的值)2 * (第五次回归的值)1 = 2
- 第三次回归:(第三次递推的值)3 * (第四次回归的值)2 = 6
- 第四次回归:(第二次递推的值)4 * (第三次回归的值)6 = 24
- 第五次回归:(第一次递归的值)5 * (第二次回归的值)24 = 120
- 到此递归函数已经拿到返回值120了,与传入的实参相乘即6*120=600
- 或者可以看成回归是这样的:
return 6*120*24*6*2*1。
3.3.以常规循环实现阶乘算法
def factorial(num):
#判断传入的参数是否不等于1
while num != 1:
#将传入的实参赋值给numfac变量,用于做阶乘(n-1)!公式
numfac = num
#如果numfac的值不为1,则开始循环
while numfac != 1:
#每次循环都将numfac的值减1,然后再赋值给numfac变量,直到numfac=1时,退出循环,这里对应的阶乘公式为(n-1)!
numfac = numfac - 1
#每次循环时都将numfac与num形参相乘,这里对应阶乘的公式n*(n-1)!
num = num * numfac
#循环完后,实参的阶乘就计算完毕了,返回
return num
#如果等于1,则直接返回1
else:
return 1
print(factorial(6))
print(factorial(600))

以传入实参6位里,我们来推理函数的运行过程:
-
1)首先判断实参6是否不等于1,如果不等于1则执行外层循环体,否则将直接返回1。
-
2)外层循环开始第一次循环,将传入的实参6赋值给numfac变量,然后开始执行内层循环体:
-
1、开始第一次内层循环,numfac值为6,不等于1,条件成立,将numfac的值减1,也就是6-1=5,此时numfac的值为5,num形参对应的实参为6,然后将实参6与numfac的值5相乘,再赋值给num变量。
-
2、开始第二次内层循环,numfac此时的值为5,不等于1,条件成立,将numfac的值减1,也就是5-1=4,此时numfac的值为4,num变量值经过上次计此时为30,然后将num变量值30与numfac的值4相乘,再赋值给num变量。
-
3、开始第三次内层循环,numfac此时的值为4,不等于1,条件成立,将numfac的值减1,也就是4-1=3,此时numfac的值为3,num变量值经过上次计此时为120,然后将num变量值120与numfac的值3相乘,再赋值给num变量。
-
4、开始第四次内层循环,numfac此时的值为3,不等于1,条件成立,将numfac的值减1,也就是3-1=2,此时numfac的值为2,num变量值经过上次计此时为360,然后将num变量值360与numfac的值2相乘,再赋值给num变量。
-
5、开始第五次内层循环,numfac此时的值为2,不等于1,条件成立,将numfac的值减1,也就是2-1=1,此时numfac的值为1,num变量值经过上次计此时为720,然后将num变量值720与numfac的值1相乘,再赋值给num变量。
-
6、开始第六次内层循环,numfac地址的值为1,1等于1,条件不成立,内层循环结束。
-
-
3)执行完内层循环体之后,直接返回此时num变量的值,这个值就是实参阶乘的结果,不能使外层循环再循环一次,否则算法就不对了。
4.使用递归函数计算斐波那契数列
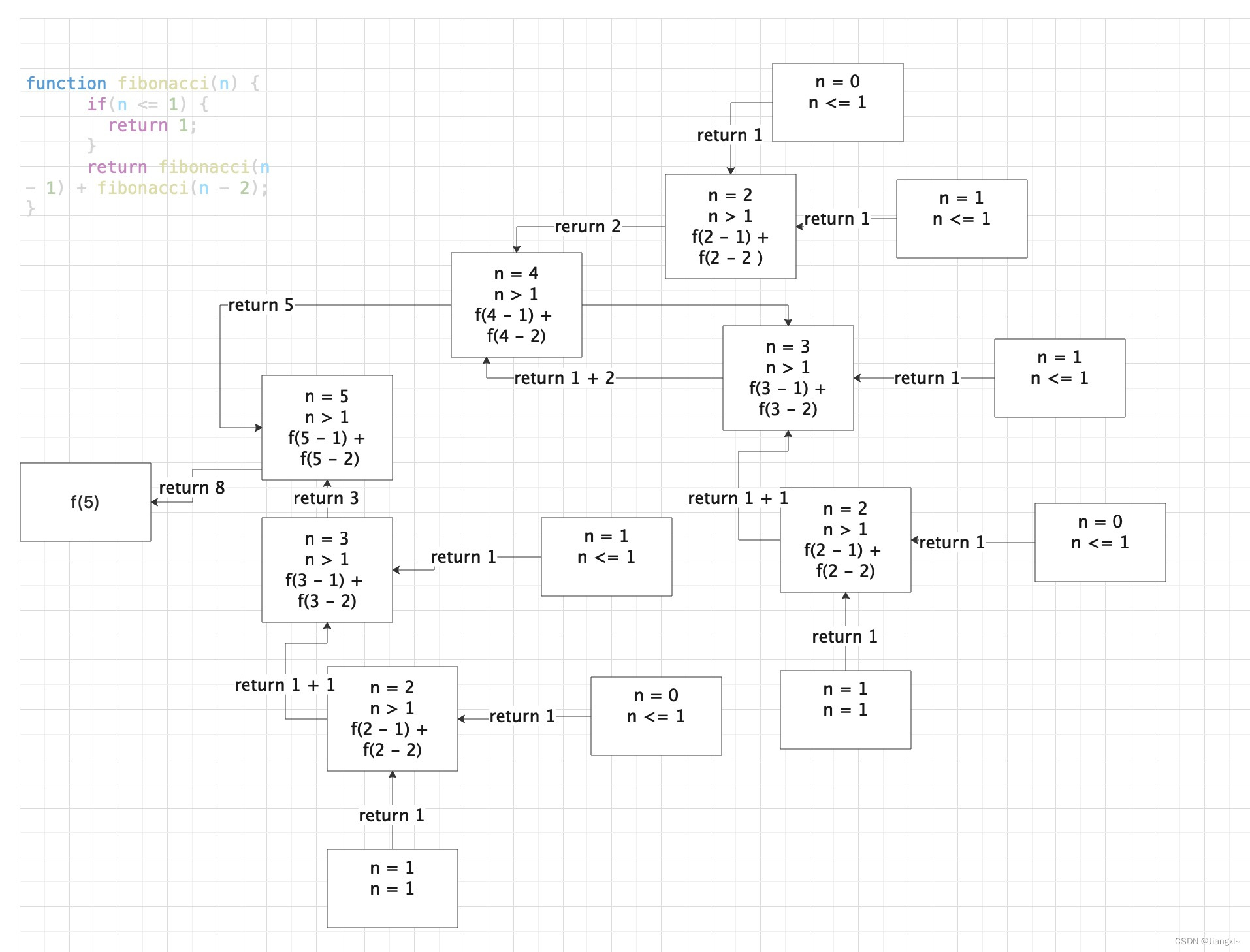
斐波那契数列(Fibonacci sequence),又称黄金分割数列,因数学家莱昂纳多·斐波那契(Leonardoda Fibonacci)以兔子繁殖为例子而引入,故又称为“兔子数列”,指的是这样一个数列:0、1、1、2、3、5、8、13、21、34、……在数学上,斐波那契数列以如下被以递推的方法定义:F(0)=0,F(1)=1, F(n)=F(n - 1)+F(n - 2)(n ≥ 2,n ∈ N*)在现代物理、准晶体结构、化学等领域
下面使用递归函数实现斐波那契数列的算法。
def fibonacci(n):
"""使用递归函数计算斐波那契数列"""
if n == 0:
return 0
if n == 1:
return 1
return fibonacci(n - 1) + fibonacci(n - 2)
我们使用fibonacci()函数来查询整数6的斐波那契数列。
print(fibonacci(6))
#输出结果8。
为什么会输出8呢?因为我输入的整数是6,在斐波那契数列中找到前6个数字,将最后两个数字相加即为8。
我们可以通过以下方法去打印出对应的斐波那契数列。
num = int(input("请输入一个数字:"))
if num <= 0:
print('请输入一个正数')
else:
for i in range(num):
print(fibonacci(i))
#print(fibonacci(6))

斐波那契数列递归流程图: