引言
现在是北京时间2023年6月13日9点11分。从决定要开始减脂之后,饥饿总是伴随着我。一觉起来肚子咕咕叫,我还是想先把文章发了再吃第一餐。燕麦加蛋白粉几乎伴随了我大学的第一年早饭。昨天练了一个小时背,练背后还做了45分钟有氧。空腹训练没有影响我的训练状态。这一点我还是比较舒服的。坚持锻炼是一个不错的习惯也恳请你务必多多锻炼自己的身体,身体就是自己最宝贵的财富。

前言
本篇文章讲解的主要是二叉树的结构以及操作,对于学习二叉树来说先了解它的使用,再回过头去学习它的底层原理等效果会更好。所以,我就简单模拟实现了一个简单二叉树,等结构和用法都了解的差不多了再研究二叉树真正创建的方式。
typedef int BTDataType;
typedef struct BinaryTreeNode
{
struct BinaryTreeNode* left;
struct BinaryTreeNode* right;
BTDataType data;
}BTNode;
BTNode* BuyNode(BTDataType x)
{
BTNode* node = (BTNode*)malloc(sizeof(BTNode));
if (node == NULL)
{
perror("malloc fail");
return NULL;
}
node->data = x;
node->left = NULL;
node->right = NULL;
return node;
}
BTNode* CreatTree()
{
BTNode* node1 = BuyNode(1);
BTNode* node2 = BuyNode(2);
BTNode* node3 = BuyNode(3);
BTNode* node4 = BuyNode(4);
BTNode* node5 = BuyNode(5);
BTNode* node6 = BuyNode(6);
BTNode* node7 = BuyNode(7);
node1->left = node2;
node1->right = node4;
node2->left = node3;
node4->left = node5;
node4->right = node6;
node3->right = node7;
return node1;
}
简单回顾
这里简单回顾一下二叉树的概念。二叉树又分为空二叉树和非空二叉数两种。非空二叉树有两个部分构成:根和子树,子树又可以分成根和子树。
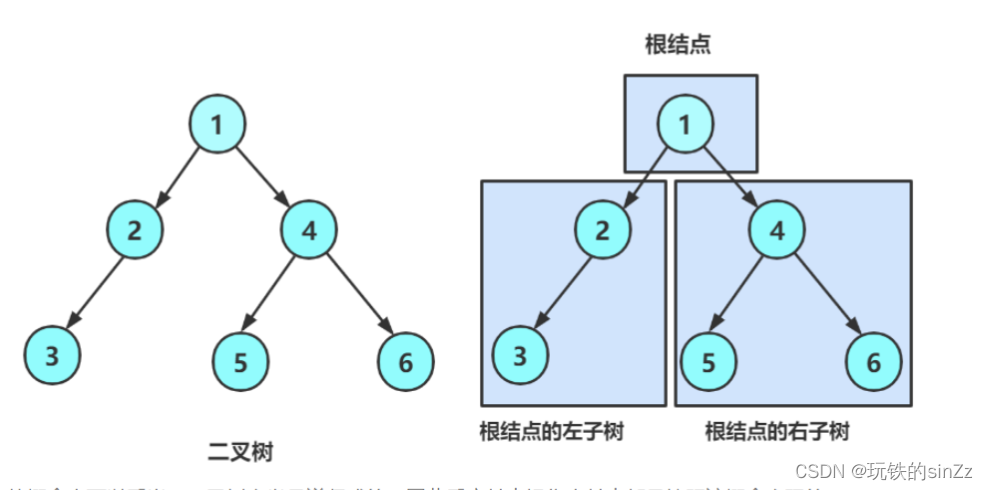
二叉树的遍历
二叉树的遍历大致分为四种,前序遍历、中序遍历、后序遍历、层序遍历。下面我们就了解一下各种的遍历方式。
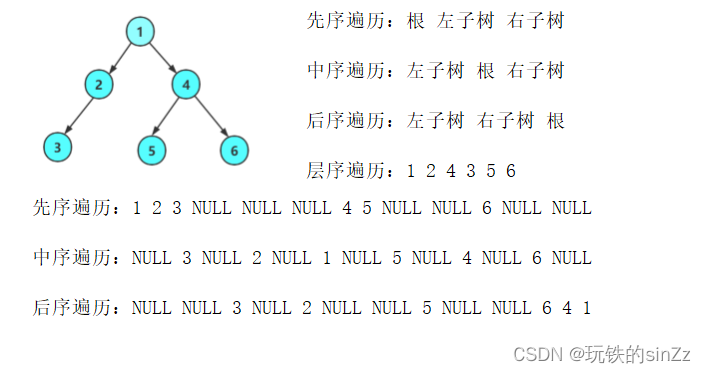
前序遍历
实现思路大致如下,采取递归的思想进行遍历。递归的结束条件为遍历的结点为空就结束。
void PreOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
printf("%d ",root->data);
PreOrder(root->left);
PreOrder(root->right);
}

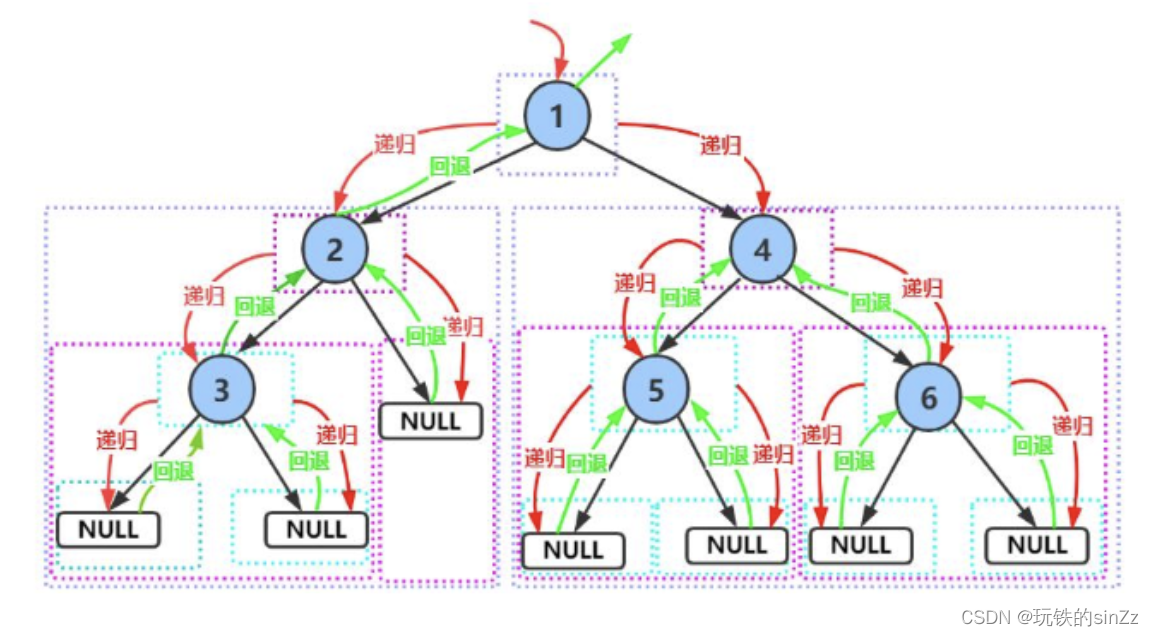
中序遍历
与前序遍历的的代码逻辑大致一样,只是访问根的顺序时机不同。本质上还是一样的思想。
void InOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
InOrder(root->left);
printf("%d ", root->data);
InOrder(root->right);
}

后序遍历
void PosOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
PosOrder(root->left);
PosOrder(root->right);
printf("%d ", root->data);
}

求树结点总数
求节点的总个数的思路就是用分治的思想。只要节点不为NULL就表示有一个结点,然后将左右子树的结点总数的和加上1(1即根结点)就能求出当前结点的总数。二叉树是可以不断地拆分成根和左右子树的,其实递归的核心就是处理一个个与原问题类似的子问题。
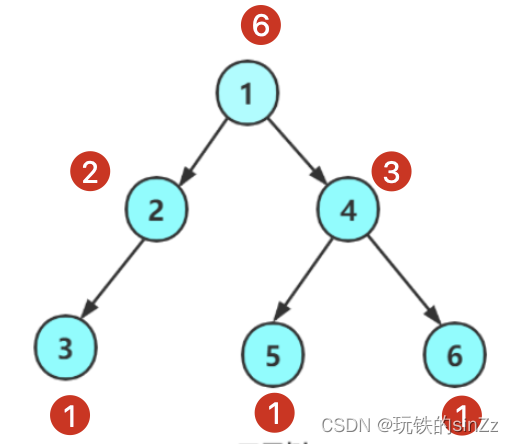
int TreeSize(BTNode* root)
{
return root == NULL ?
0 :
TreeSize(root->left)
+TreeSize(root->right)
+1;
}

求树的高度
求树的高度也可以采取分治的思路。如果说上面的求结点总数是校长求全校的人数,那么求树的高度其实就是找全校最高的人。实现思路如下,找左右子树中较大的那个加上根节点的高度就是树的高度。
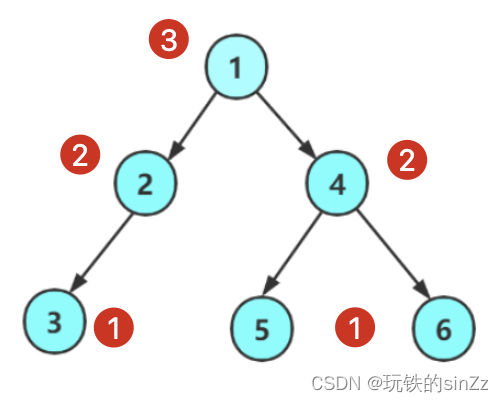
int TreeHeight(BTNode* root)
{
if(root == NULL)
return 0;
int lh =TreeHeight(root->left);
int rh =TreeHeight(root->right);
return lh > rh ? lh+1 : rh+1;
}

求第k层节点个数
求第k层的结点个数本质就是求左子树第k-1个结点个数+右子树第k-1层结点个数的和。
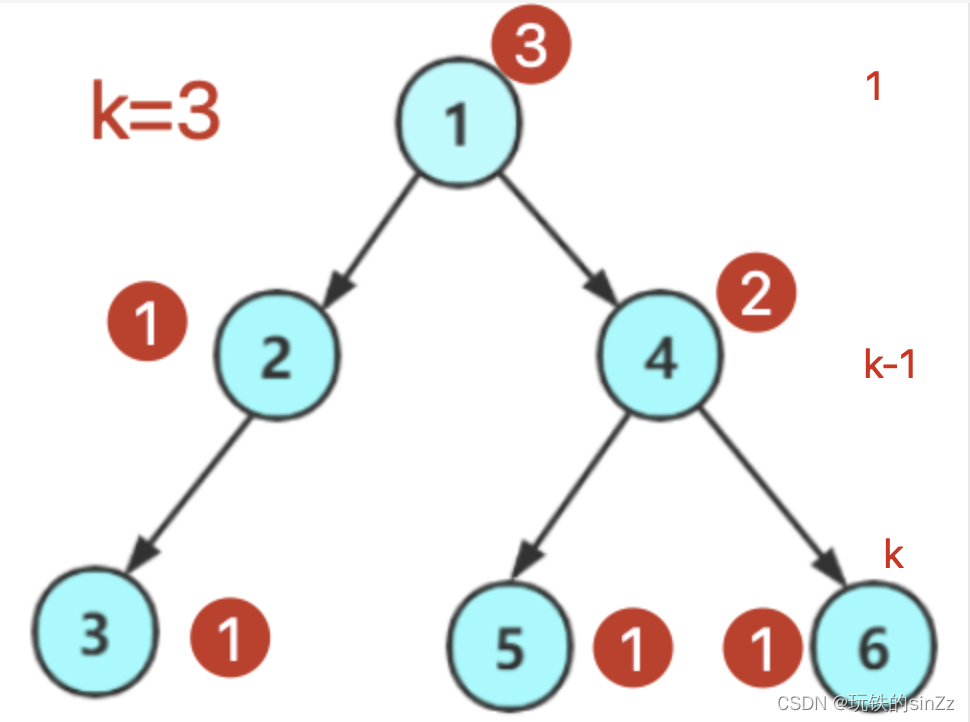
int TreeKLevel(BTNode* root, int k)
{
if(root == NULL)
return 0;
if(k == 1)
return 1;
int lk = TreeKLevel(root->left, k-1);
int rk = TreeKLevel(root->right, k-1);
return lk+rk;
}

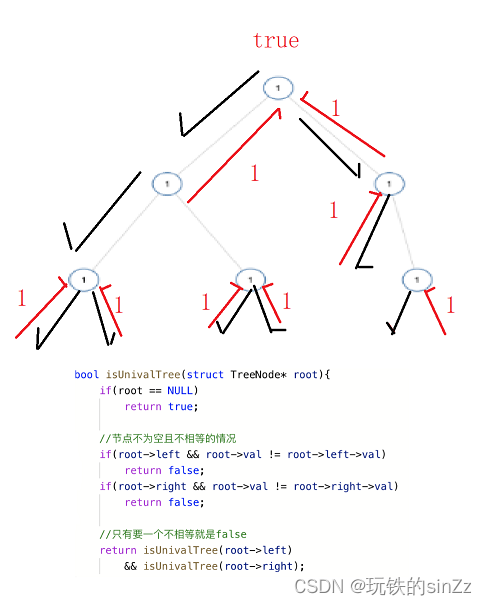
单值二叉树问题

本题的解题的思路有很多,如遍历、分治等。当然这里比较推荐实用分治的思想来进行解决这种二叉树的很多问题中,遍历的结局思路是不如分治的。下面就简单的介绍一下思路。首先,要将结点为空的情况考虑进去。其次,判断左右子结点是否存在且值不相等的情况。最后,分治递归进行比较判断,只要有一个不相等整体就是不为等值二叉树。

二叉树的查找
二叉树的查找接口,它的作用不仅仅是查找到该结点,还可以作为获取想要修改结点的地址的一个方式。实现思路主要是以递归的思想进行遍历整棵树。如果结点的值==val,那就返回这个结点的地址。
BTNode* BTFind(BTNode* root, int x)
{
if(root == NULL)
{
return NULL;
}
//判断
if(root->data == x)
return root;
//NULL不返回,找到了才返回
BTNode* lret = BTFind(root->left, x);
if(lret)
return lret;
BTNode* rret = BTFind(root->right, x);
if(rret)
return rret;
//走到此处表示没有找到结点
return NULL;
}
相同二叉树
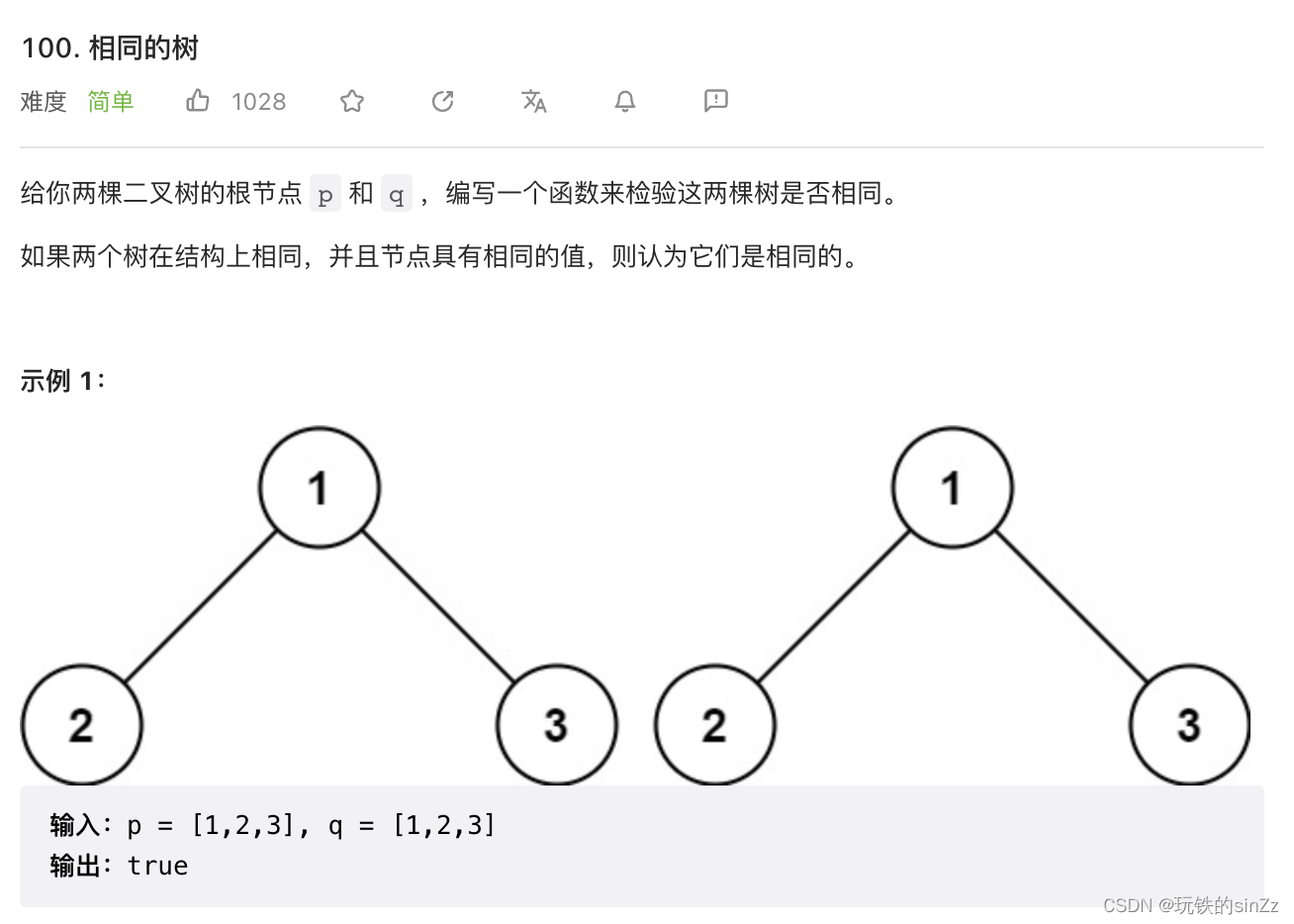
解决本问题的思路如下,首先,考虑根节点都为空的情况以及其中是一个根结点为空的情况下。然后递归判断左右子树值是否相等即可。

前序遍历oj
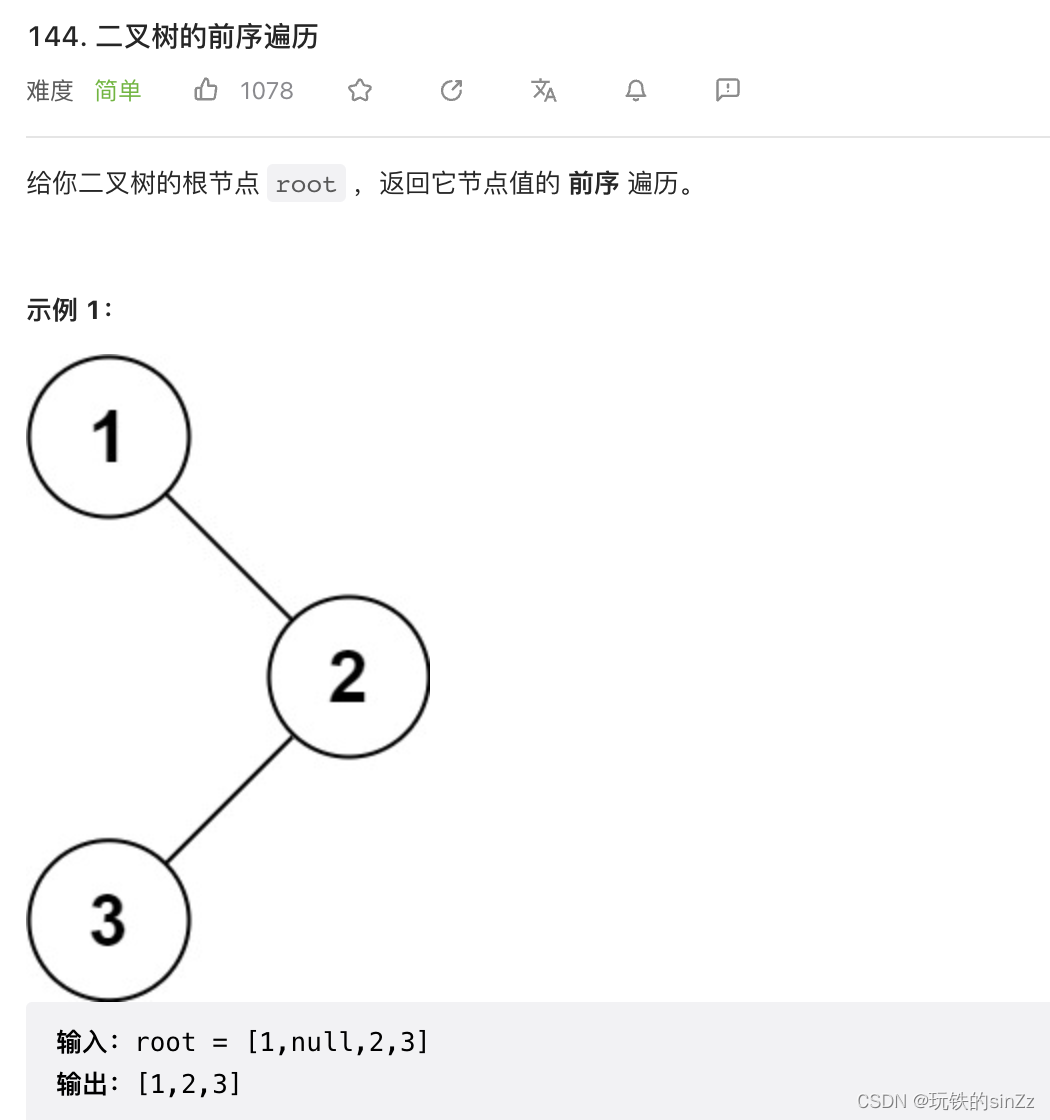
主要介绍的是接口型oj的特点。这里的returnSize是一个输出型参数,传递的局部变量标识数组长度变量的地址,要求我们写入动态开辟数组的长度。作为返回值的数组要用存放在堆区(动态申请)的数组。若使用局部定义的数组,在函数调用结束后就会销毁,就无法的到遍历后的结果,也会有野指针问题。
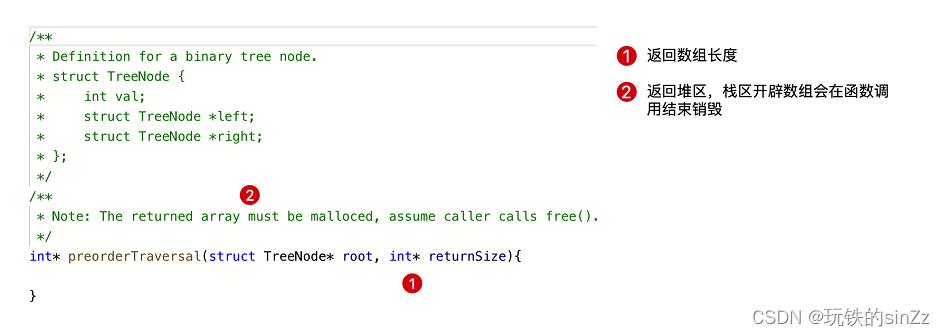
解题思路如下,先求出树的结点总数,然后,根据树的结点总数来malloc申请空间。最后,在创建一个局部变量来作为标记数组下标,前序遍历将数据写入数组中。

另一棵树的子树
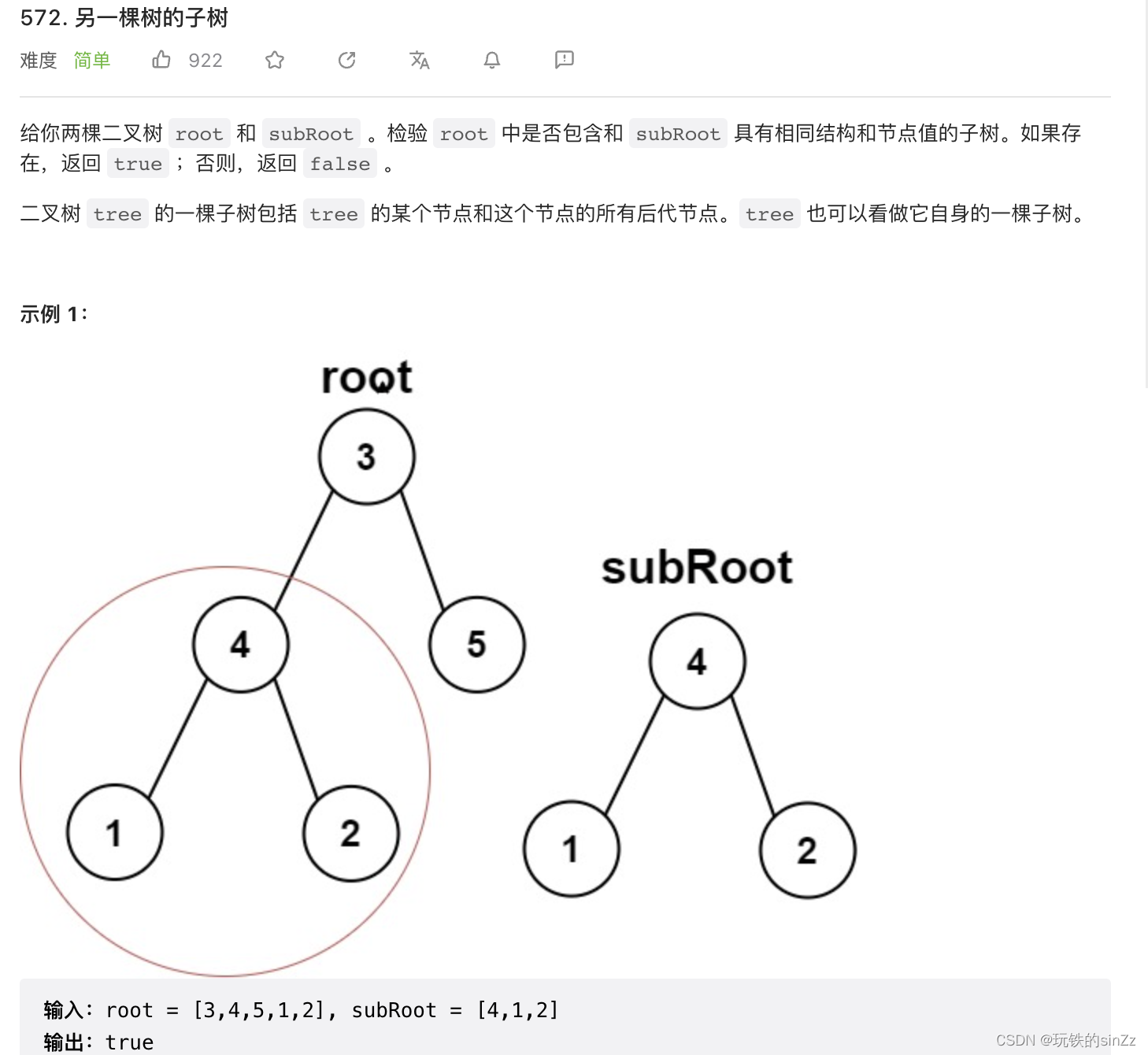
解题思路如下,首先,root == NULL时,那就不可能是匹配和subRoot的一样的子树。然后,这里可以复用之前写的判断两树是否相同的代码,用每个根节点进行匹配,然后,递归分治找到匹配的子树就返回真,否则返回假。

层序遍历
二叉树的层序遍历实现思路如下,将根节点入队列,遍历根节点后,判断根的左右节点是否为NULL,不为NULL就入队列。循环往复直到队列为空就结束层序遍历。点击获取队列实现代码。
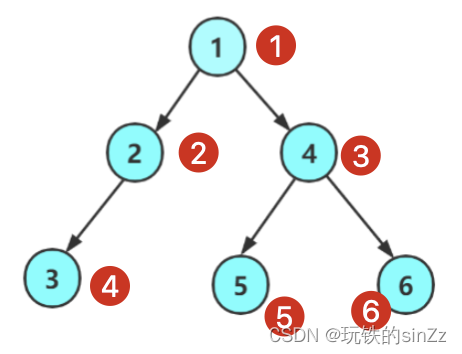


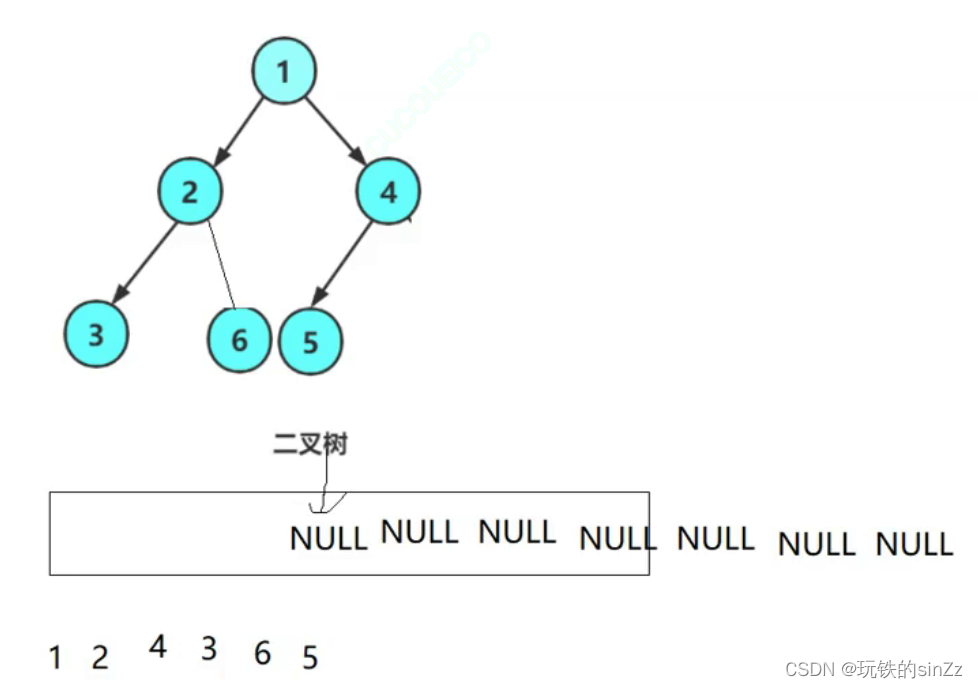
判断是否为完全二叉树
本接口实现主要思路是根据层序遍历,完全二叉树第一个NULL结点后面不会出现非空结点。实现步骤依旧是层序遍历的思路,当出到第一个NULL结点时,便不再让数据入队,遍历剩下的结点。当出现非空结点即表示不是完全二叉树,若全为空结点则表示为完全二叉树。

二叉树的销毁
采取后序遍历的思想进行对节点的释放。这里实现的版本为一级指针作为参数,需要调用本函数后手动置空。