PTA 7-251 汉诺塔问题

分数 100
作者 于延
单位 哈尔滨师范大学

任务描述
在印度，有这么一个古老的传说：在世界中心贝拿勒斯（在印度北部）的圣庙里，一块黄铜板上插着三根宝石针。印度教的主神梵天在创造世界的时候，在其中一根针上从下到上地穿好了由大到小的64片金片，这就是所谓的汉诺塔(Tower of Hanoi)。不论白天黑夜，总有一个僧侣在按照下面的法则移动这些金片到另一根针上。法则是一次只移动一片，而且小片必在大片上面。当所有的金片都从梵天穿好的那根针上移到第三根针上时，世界就将在一声霹雳中消灭，梵塔、庙宇和众生都将同归于尽。

利用数学方法可以计算得出，若传说属实，僧侣们需要264−1步才能完成这个任务。若他们每秒可完成一次盘子的移动，就需要5849亿年才能完成。整个宇宙现在也不过137亿年。

这就是关于汉诺塔传说，由此衍生出汉诺塔问题，这个问题看起来好像有点复杂，实际上可以用递归的思想来分析：

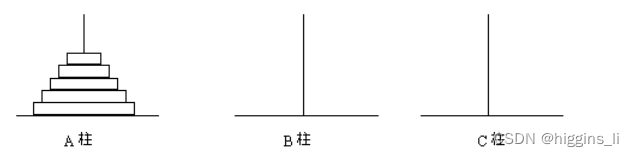
将n个盘子从A柱移到C柱可以分解为下面三个步骤：

（1）将A柱上的n-1个盘子借助于C柱移到B柱上；

（2）将A柱上的最后一个盘子移到C柱上；

（3）再将B柱上的n-1盘子借助于A柱移到C柱上。

其中，第一步又可以分解为以下三步：

（1）将A柱上的n-2个盘子借助于B柱移到C柱上；

（2）将A柱上的第n-1个盘子移到B柱上；

（3）再将C柱上的n-2个盘子借助于A柱移到B柱上。

这种分解可以一直递归地进行下去，直到变成移动一个盘子，递归结束。事实上，以上三个步骤包含两种操作：

（1）将多个盘子从一根柱子移到另一根柱子上，这是一个递归的过程；

（2）将一个盘子从一根柱子移到另一根柱子。

分别编写两个函数来实现以上两个操作。

函数hanoi（int n,char one,char two,char three）实现把"one"柱上的n个盘子借助于"two"柱移到"three"柱上；

函数move(char x,char y)表示将1个盘子从x柱移到y柱，并输出移动盘子的提示信息。

编程输入金盘的数量n，输出将n个金盘从A柱(借助B柱)移动到C柱的过程。

输入样例:

3

输出样例:

A-->C
A-->B
C-->B
A-->C
B-->A
B-->C
A-->C

代码长度限制
16 KB
时间限制
400 ms
内存限制
64 MB

#include<stdio.h>
int main()
{
	int n=0;
	char a='a',b='b',c='c';
	scanf("%d %c %c %c",&n,&a,&b,&c);
	
	hanoi(n,a,b,c);
}
 
void hanoi(int n,char a,char b,char c)
{
	if(n==1)
    {
		printf("%c-->%c\n",a-32,c-32);
	}
	else
    {
		hanoi(n-1,a,c,b);
		printf("%c-->%c\n",a-32,c-32);
		hanoi(n-1,b,a,c);
	}
}