A - Water Station(模拟)

题意：在[0,100]所有 x % 5 == 0的地方设置一个水站，给你一个位置x，问最近的水站的坐标，考虑余数即可。

#include <bits/stdc++.h>
#define ll long long
#define inf 0x3f3f3f3f
using namespace std;
const int N = 2e6 + 5;
#define sq(x) (x) * (x)
void solve() {
	int n;
	cin >> n;
	int r = n % 5;
	if (r == 0) cout << n << '\n';
	else if (r < 3) cout << n - r << '\n';
	else cout << n + 5 - r << '\n';
}
int main() {
	ios::sync_with_stdio(false);
	cin.tie(0);
	int T = 1;
//	cin >> T;
	while (T--) {
		solve();
	}
	return 0;
}

B - ABCDEFG（模拟）

题意：给出相邻点距离，让你查询某个线段的距离。
思路：模拟逐步接近即可。

#include <bits/stdc++.h>
#define ll long long
#define inf 0x3f3f3f3f
using namespace std;
const int N = 2e6 + 5;
#define sq(x) (x) * (x)
void solve() {
	char p, q;
	map<char, int> mp; 
	mp['A'] = 3;
	mp['B'] = 1;
	mp['C'] = 4;
	mp['D'] = 1;
	mp['E'] = 5;
	mp['F'] = 9;
	cin >> p >> q;
	if (p > q) swap(p, q);
	int ans = 0;
	while (p < q) {
		ans += mp[p];
		p++;
	}
	cout << ans << '\n';
}
int main() {
	ios::sync_with_stdio(false);
	cin.tie(0);
	int T = 1;
//	cin >> T;
	while (T--) {
		solve();
	}
	return 0;
}

C - Snuke the Cookie Picker(模拟、暴力)

题意：原本有一个长宽至少为2的‘#’矩阵，被其中一个变成了’.'，问你那个位置在哪里。
思路：不管去掉哪个，我们保证可以找到最上面的坐标，最下面的坐标，最左边的坐标，最右边的坐标，因为这是至少2*2。

#include <bits/stdc++.h>
#define ll long long
#define inf 0x3f3f3f3f
using namespace std;
const int N = 2e6 + 5;
#define sq(x) (x) * (x)
char mp[505][505];
void solve() {
	int h, w;
	cin >> h >> w;
	for (int i = 1; i <= h; i++) {
		for (int j = 1; j <= w; j++) {
			cin >> mp[i][j];
		}
	}
	int l = 1000, r = 0;
	int u = 1000, d = 0;
	for (int i = 1; i <= h; i++) {
		for (int j = 1; j <= w; j++) {
			if (mp[i][j] == '.') continue;
			l = min(l, j);
			r = max(r, j);
			u = min(u, i);
			d = max(d, i);
		}
	}
	for (int i = u; i <= d; i++) {
		for (int j = l; j <= r; j++) {
			if (mp[i][j] == '.') {
				cout << i << ' ' << j << '\n';
			}
		}
	} 
}
int main() {
	ios::sync_with_stdio(false);
	cin.tie(0);
	int T = 1;
//	cin >> T;
	while (T--) {
		solve();
	}
	return 0;
}

D - Sleep Log（二分，前缀）

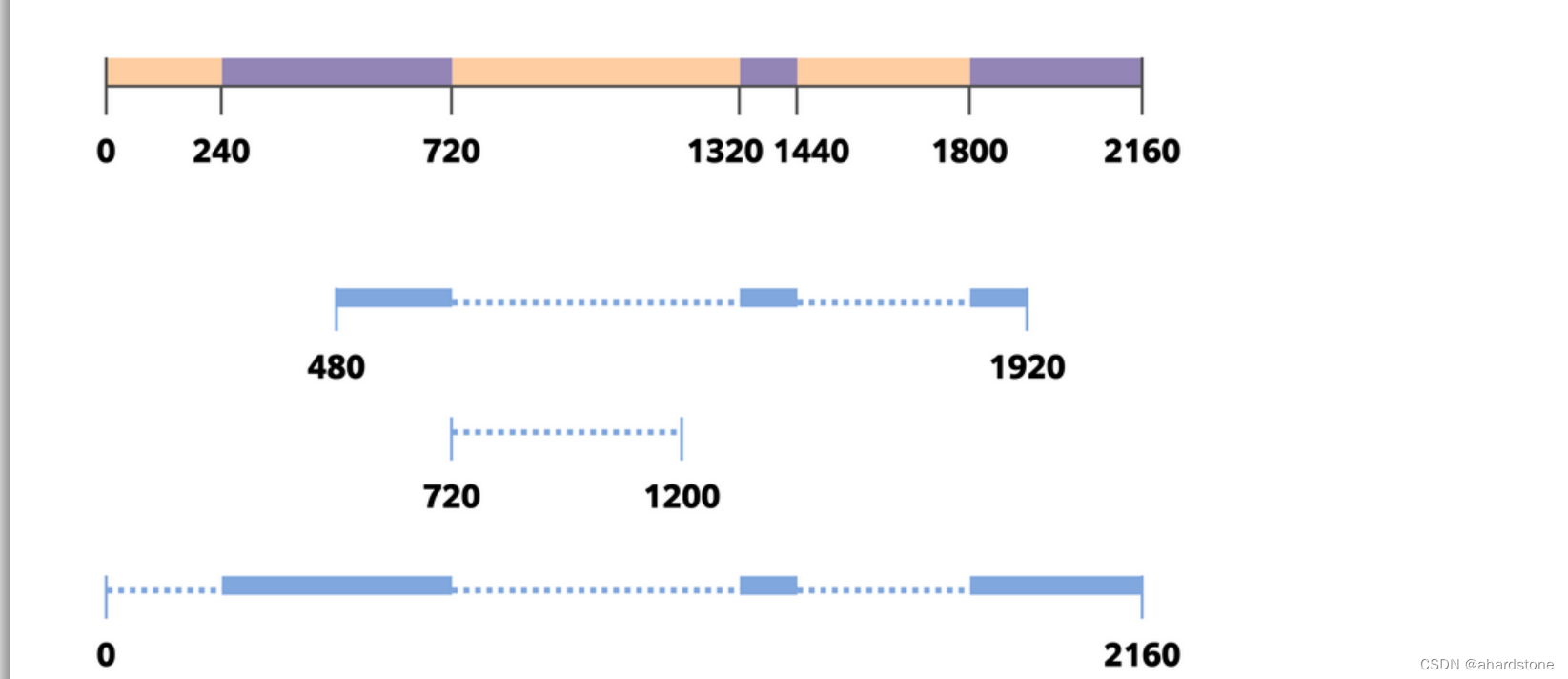
在这里插入图片描述
题意：某个人会在奇数位置醒来，偶数位置睡觉，接下来，每个询问查询一下这个区间内的睡觉时间。
思路：可以通过前缀和解决某个节点前缀时间，进而求出区间时间。我们需要二分查找最近的点。这里有一点点细节，分两种情况，先考虑简单的情况，就是l，r之间至少有一个节点，我们之间二分查找到l右侧第一个点，r右侧第一个点，然后减去r 到右侧第一个点的部分，补上l到右侧第一个点的部分。第二种情况是，l，r之间没有节点的情况，如果l刚好在，节点上，那么r如果也在节点上，查出来的两个最近点的位置是一样的，考虑这个点是奇数位置还是偶数位置，如果说，l在节点上，r不在节点上，查出来刚好差一个点，我们考虑，l右侧的第一个是奇数位置还是偶数位置。如果l，r均不在，查出来也是一样的，考虑这个点是奇点还是偶点，发现其实可以和第一张并上去。

#include <bits/stdc++.h>
#define ll long long
#define inf 0x3f3f3f3f
using namespace std;
const int N = 2e5 + 5;
int a[N];
ll sum[N];
void solve() {
	int n;
	cin >> n;
	for (int i = 1; i <= n; i++) cin >> a[i];
	for (int i = 2; i <= n; i++) {
		if (i % 2) sum[i] = sum[i - 1] + (a[i] - a[i - 1]);
		else sum[i] = sum[i - 1];
	}
//	for (int i = 1; i <= n; i++) cout << sum[i] << ' ';
//	cout << '\n';
	int q;
	cin >> q;
	while (q--) {
		int x, y;
		cin >> x >> y;
		int l = lower_bound(a + 1, a + 1 + n, x) - a;
		int r = lower_bound(a + 1, a + 1 + n, y) - a;
		ll tmp = sum[r] - sum[l];
		if (l == r) {
			if (r % 2) cout << y - x << '\n';
			else cout << 0 << '\n';
			continue;
		}
		if (l + 1 == r) {
			if (a[l] == x) {
				if (l % 2 == 0) cout << y - x << '\n';
				else cout << 0 << '\n';
				continue;
			}
		}
		if (r % 2) tmp -= a[r] - y;
		if (l % 2) tmp += a[l] - x;
		cout << tmp << '\n';
	}
}
int main() {
	ios::sync_with_stdio(false);
	cin.tie(0);
	int T = 1;
//	cin >> T;
	while (T--) {
		solve();
	}
	return 0;
}