学习目标：

1. 学习基本概念：首先，了解逻辑代数的基本概念和术语，如命题、逻辑运算符（与、或、非等）、真值表等。确保你对这些基本概念有清晰的理解。

2. 学习基本公式：研究逻辑代数的基本公式，如否定律、交换律、结合律、分配律和吸收律等。理解这些公式的含义和应用场景，以及它们在逻辑推理和表达式简化中的作用。

3. 练习推导证明：通过练习推导和证明基本公式，加深对其逻辑性和正确性的理解。可以通过构建真值表、使用公式化简规则或采用形式化证明方法等来进行练习。

4. 学习常用公式：学习逻辑代数中的常用公式，如德摩根定律、等价关系、充要条件等。这些公式在逻辑推理和逻辑表达式的转换中非常有用。

5. 解决问题和应用：通过解决实际问题和应用场景，将逻辑代数的公式应用到实际情境中。可以通过逻辑推理问题、布尔代数表达式求解和逻辑电路设计等来加深对公式的理解。

6. 寻求参考资料和教学资源：查阅相关的教科书、学术论文、在线教程和视频教程等，以获取更深入的知识和实例。

7. 练习和实践：进行大量的练习和实践，通过解题和应用来巩固对逻辑代数公式的掌握。实践是学习的关键，通过不断应用公式，你将更加熟练和自信。

请注意，逻辑代数是一门抽象的数学学科，对于初学者可能需要花费一些时间和精力来理解和应用。但随着学习的深入和实践的积累，你会逐渐掌握逻辑代数的基本公式和常用公式，并能灵活运用于实际问题中。

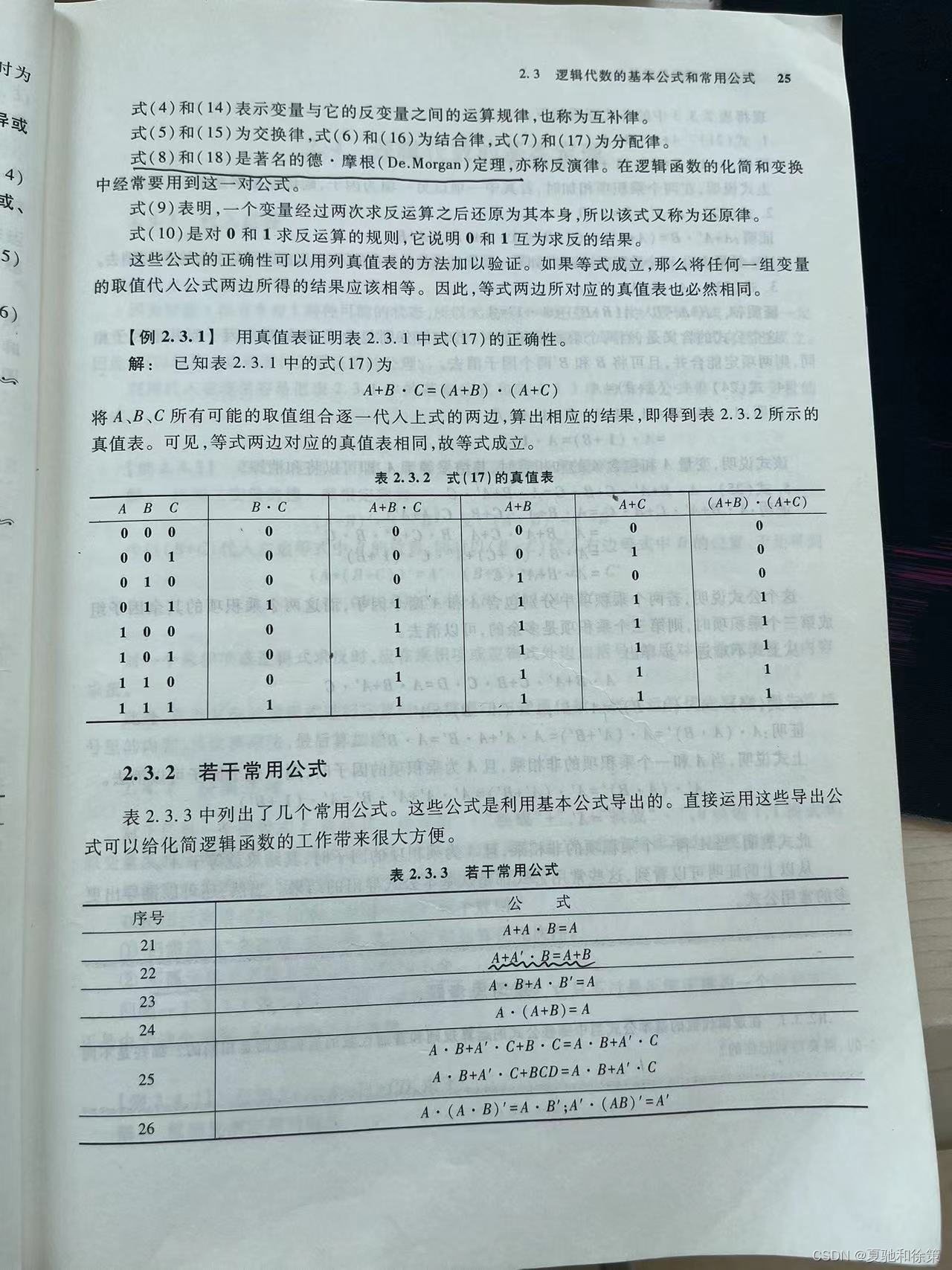
2.3.1 基本公式

逻辑代数是一种应用于逻辑和布尔代数的数学体系，用于处理逻辑关系和逻辑运算。它基于布尔代数的原理和规则，通过逻辑公式和运算符来描述和操作逻辑关系。

以下是逻辑代数中的几个基本公式和运算规则：

1. 否定律（Negation Laws）：
- 否定的否定（Double Negation）：¬(¬P) = P

2. 交换律（Commutative Laws）：
- 与运算的交换律（AND Commutative）：P ∧ Q = Q ∧ P
- 或运算的交换律（OR Commutative）：P ∨ Q = Q ∨ P

3. 结合律（Associative Laws）：
- 与运算的结合律（AND Associative）：(P ∧ Q) ∧ R = P ∧ (Q ∧ R)
- 或运算的结合律（OR Associative）：(P ∨ Q) ∨ R = P ∨ (Q ∨ R)

4. 分配律（Distributive Laws）：
- 与运算对于或运算的分配律（AND over OR）：P ∧ (Q ∨ R) = (P ∧ Q) ∨ (P ∧ R)
- 或运算对于与运算的分配律（OR over AND）：P ∨ (Q ∧ R) = (P ∨ Q) ∧ (P ∨ R)

5. 吸收律（Absorption Laws）：
- 与运算对于或运算的吸收律（AND Absorption）：P ∧ (P ∨ Q) = P
- 或运算对于与运算的吸收律（OR Absorption）：P ∨ (P ∧ Q) = P

这些基本公式和运算规则是逻辑代数的基石，它们提供了一种描述和操作逻辑关系的数学框架。在逻辑推理、布尔代数、电路设计和计算机科学等领域中，这些公式和规则被广泛应用于逻辑运算、表达式简化和问题求解。

2.3.2 若干常用公式

当根据基本公式进行推导时，可以应用一些常见的推导技巧和逻辑运算规则来得到常用公式。以下是一些常见的公式和它们的推导过程：

1. 德摩根定律：
- ¬(P ∧ Q) = ¬P ∨ ¬Q（德摩根第一定律）
- ¬(P ∨ Q) = ¬P ∧ ¬Q（德摩根第二定律）

这些定律可以通过使用交换律和否定律进行推导。

2. 分配律：
- P ∧ (Q ∨ R) = (P ∧ Q) ∨ (P ∧ R)（与运算对于或运算的分配律）
- P ∨ (Q ∧ R) = (P ∨ Q) ∧ (P ∨ R)（或运算对于与运算的分配律）

这些定律可以通过使用分配律和结合律进行推导。

3. 吸收律：
- P ∧ (P ∨ Q) = P（与运算对于或运算的吸收律）
- P ∨ (P ∧ Q) = P（或运算对于与运算的吸收律）

这些定律可以通过使用分配律和结合律进行推导。

4. 等价关系：
- P → Q = ¬P ∨ Q（蕴含的等价形式）
- P ↔ Q = (P → Q) ∧ (Q → P)（双向蕴含的等价形式）

这些等价形式可以通过应用蕴含的定义和德摩根定律进行推导。

这只是一些常见公式的示例，逻辑代数还包含许多其他公式和定律。通过灵活运用基本公式和逻辑运算规则，你可以进一步推导出更多的常用公式。记住，练习和实践是熟练运用逻辑代数的关键。

复习思考题

R2.3.1 在逻辑代数的基本公式当中哪些公式的运算规则和普通代数的运算规则是i相同的？哪些是不同的需要特别记住？

在逻辑代数的基本公式中，有一些运算规则与普通代数的基本规则相同，而其他一些规则则是不同的，需要特别记住。下面是对比普通代数和逻辑代数的一些运算规则：

相同的运算规则：
1. 交换律：对于与运算和或运算，交换律在普通代数和逻辑代数中都适用。
2. 结合律：对于与运算和或运算，结合律在普通代数和逻辑代数中都适用。
3. 分配律：在普通代数和逻辑代数中，分配律适用于与运算和或运算之间的关系。

不同的运算规则：
1. 否定律：在逻辑代数中，存在否定运算符（¬）用于取反。这是逻辑代数独有的运算规则，普通代数中没有对应的取反操作。
2. 吸收律：在逻辑代数中，存在吸收律，表示与运算对于或运算或者或运算对于与运算的吸收性。这也是逻辑代数独有的运算规则，普通代数中没有对应的吸收律。

需要特别记住的规则：
1. 德摩根定律：德摩根定律是逻辑代数中非常重要的定律，描述了与运算和或运算的取反形式。记住德摩根定律对于进行逻辑表达式的化简和推导非常有帮助。
2. 等价关系：在逻辑代数中，等价关系指的是逻辑等价和蕴含的关系。了解等价关系的定义和性质，以及相应的运算规则，有助于理解逻辑推理和逻辑表达式之间的关系。

需要注意的是，虽然有些运算规则在普通代数和逻辑代数中相同，但在逻辑代数中它们具有特定的含义和应用。因此，当应用运算规则时，需要注意上下文和运算符的逻辑意义。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/637948.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！