Linear Regression

您将使用一个变量实现线性回归，以预测餐厅特许经营的利润。

1 导包

首先，让我们运行下面的单元格来导入此任务中所需的所有包。

• numpy 是在 Python 中处理矩阵的基本包。
• matplotlib 是 Python 中绘制图形的著名库。
• utils.py 包含此任务的辅助功能。 您不需要修改此文件中的代码。

import numpy as np
import matplotlib.pyplot as plt
from utils import *
import copy
%matplotlib inline

2 - 问题陈述

假设你是一家餐厅连锁店的CEO，正在考虑在不同的城市开设新店。

• 你希望将业务扩展到可能为餐厅带来更高利润的城市。
• 该连锁店已经在各个城市有餐厅，你拥有这些城市的利润和人口数据。
• 你还有一些候选城市的数据。
  • 对于这些城市，你知道其人口。

你能否使用这些数据来帮助你确定哪些城市可能会为你的业务带来更高的利润？

3 - 数据集

你将首先加载此任务的数据集。

• 下面显示的 load_data() 函数将数据加载到变量 x_train 和 y_train 中
  • x_train 是一个城市的人口
  • y_train 是该城市餐厅的利润。 利润的负值表示亏损。
  • X_train 和 y_train 都是 numpy 数组。

# 加载数据集
x_train, y_train = load_data()

可视化数据

通过可视化了解数据通常很有用。

• 对于这个数据集，您可以使用散点图来可视化数据，因为它只有两个属性需要绘制（利润和人口）。
• 许多在现实生活中可能遇到的其他问题具有超过两个属性（例如，人口、平均家庭收入、月利润、月销售额）。当您拥有超过两个属性时，仍然可以使用散点图来查看每对属性之间的关系。

fig = plt.figure(figsize=(20,8))
plt.scatter(x_train,y_train,marker='x',c='r')
plt.rcParams['font.sans-serif']=['SimHei']
plt.title("每个城市的利润与人口")
plt.ylabel("利润（/$10,000）")
plt.xlabel("人口（/10,000s）")
plt.show()

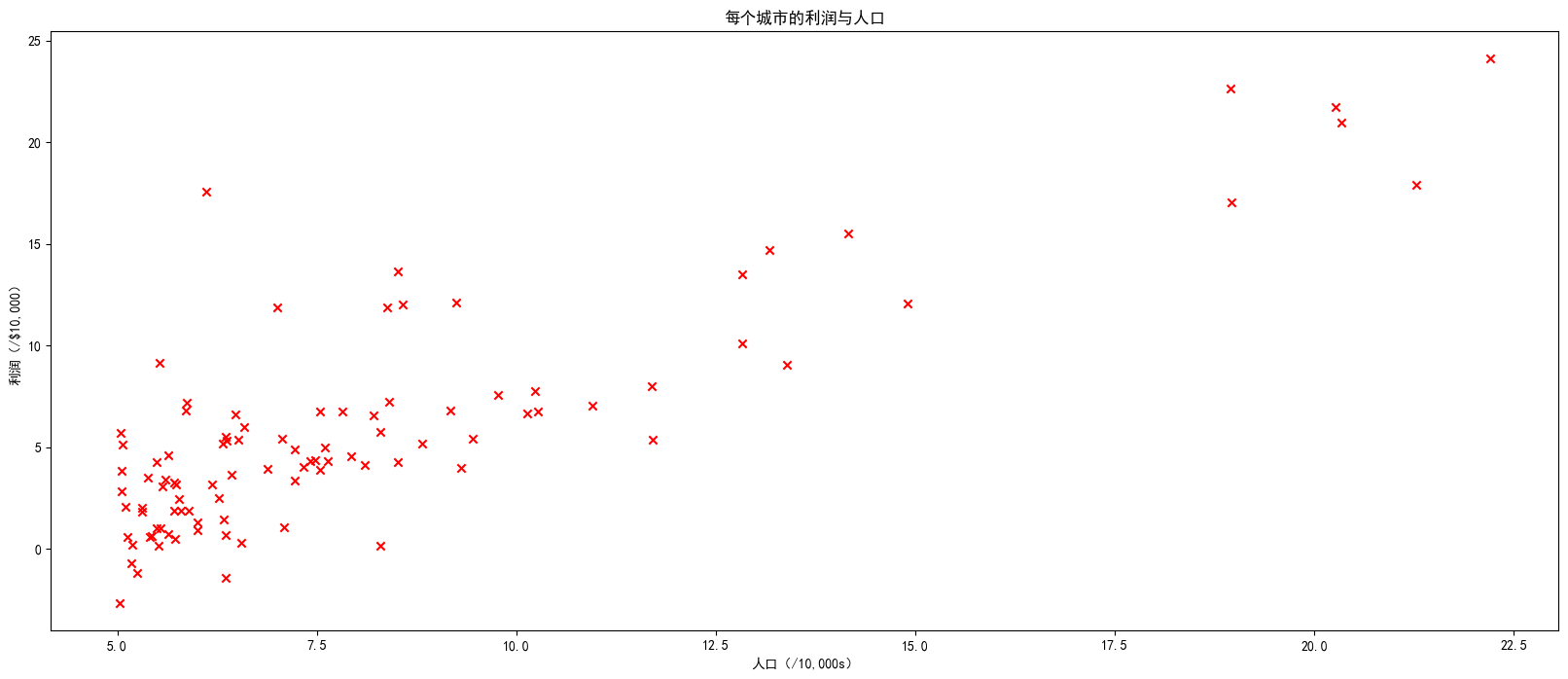
你的目标是构建一个线性回归模型来拟合这些数据。

• 通过这个模型，您可以输入一个新城市的人口，然后让模型估计该城市餐厅的潜在月利润。

4 - 线性回归复习

在这个实验室中，您将拟合线性回归参数**(w,b)**到您的数据集上。

• 线性回归模型函数是一个从 x（城市人口）映射到 y（该城市餐厅的月利润）的函数，表示为
  $$f_{w,b}(x)=wx+b$$

• 要训练线性回归模型，您想找到最适合您的数据集的**(w,b)**参数。

  • 为了比较一个 (w,b) 的选择相对于另一个选择更好或更差，您可以使用代价函数 J(w,b) 进行评估

    • J是关于 **(w,b)**的函数。也就是说，代价 J(w,b) 的值取决于 **(w,b)**的值。

  • 最适合您的数据的 **(w,b)**的选择是具有最小代价 J(w,b) 的那个。

• 要找到使代价 J(w,b) 最小的值 (w,b)，您可以使用一种称为梯度下降的方法。

  • 每次梯度下降的步骤都会使您的参数 (w,b) 接近最优值，这些最优值将实现最低代价 J(w,b)。

• 训练后的线性回归模型可以接受输入特征 x（城市人口）并输出一个预测 f_{w,b}(x)（该城市餐厅的预计月利润）。

5 - 计算代价

梯度下降涉及重复的步骤来调整您的参数 $(w,b)$ 的值，以逐渐获得更小的代价 $J(w,b)$。

• 在每个梯度下降的步骤中，通过计算代价 $J(w,b)$ 可以帮助您监视您的进展情况，因为 $(w,b)$ 被更新。
• 在本节中，您将实现一个函数来计算 $J(w,b)$，以便您可以检查您的梯度下降实现的进度。

代价函数

正如您在讲座中所记得的那样，对于一个变量，线性回归的代价函数 $J(w,b)$ 定义为

$$J(w,b)=\frac{1}{2m}\sum _{i=0}^{m-1}(f_{w,b}(x^{(i)})-y^{(i)}{)}^2$$

• 您可以将 $f_{w,b}(x^{(i)})$ 视为模型对您餐厅利润的预测，而不是数据中记录的实际利润 $y^{(i)}$。
• $m$ 是数据集中的训练示例数量。

模型预测

• 对于一个变量的线性回归模型，模型 $f_{w,b}$ 对于示例 $x^{(i)}$ 的预测表示为：

$$f_{w,b}(x^{(i)})=w{x}^{(i)}+b$$

这是一条直线的方程，具有截距 $b$ 和斜率 $w$。

实现

请完成下面的 compute_cost() 函数来计算代价 $J(w,b)$。

• 遍历训练示例，并针对每个示例计算：

  • 模型对于该示例的预测值
    $$f_{wb}(x^{(i)})=w{x}^{(i)}+b$$

  • 该示例的代价 $$cos{t}^{(i)}=(f_{wb}-y^{(i)}{)}^2$$

• 返回所有示例的总代价
  $$J(\mathbf{w},b)=\frac{1}{2m}\sum _{i=0}^{m-1}cos{t}^{(i)}$$

  • 这里，$m$ 是训练示例的数量，$\sum$ 是求和运算符

如果您遇到困难，可以在下面的单元格中查看提示，以帮助您进行实现。

def compute_cost(x,y,w,b):
    m = x.shape[0]
    total_cost = 0
    cost = 0
    for i in range(m):
        f_wb = w*x[i]+b
        cost += (f_wb-y[i])**2
    total_cost = cost/(2*m)
    return total_cost

6 - 梯度下降

在本节中，您将实现线性回归参数 $w,b$ 的梯度下降。

如视频讲座中所述，梯度下降算法如下：

重复直到收敛:    {    0000 b : = b − α ∂ J ( w , b ) ∂ b    0000 w : = w − α ∂ J ( w , b ) ∂ w    } \begin{align*}& \text{重复直到收敛:} \; \lbrace \; & \phantom {0000} b := b - \alpha \frac{\partial J(w,b)}{\partial b} \; & \phantom {0000} w := w - \alpha \frac{\partial J(w,b)}{\partial w} \tag{1} \; & & \rbrace\end{align*} ​重复直到收敛:{​0000b:=b−α∂b∂J(w,b)​​0000w:=w−α∂w∂J(w,b)​​​}​(1)​
在此公式中，参数 w, b 同时更新，其中
$$\frac{\partial J(w,b)}{\partial b}=\frac{1}{m}\sum _{i=0}^{m-1}(f_{w,b}(x^{(i)})-y^{(i)})\text{\hspace{1em}(2)}$$
$$\frac{\partial J(w,b)}{\partial w}=\frac{1}{m}\sum _{i=0}^{m-1}(f_{w,b}(x^{(i)})-y^{(i)})x^{(i)}\text{\hspace{1em}(3)}$$

• m 是数据集中的训练示例数量

• $f_{w,b}(x^{(i)})$是模型的预测值，而 $y^{(i)}$ 是目标值

您将实现一个名为 compute_gradient 的函数，该函数计算 $\frac{\partial J(w)}{\partial w}$，$\frac{\partial J(w)}{\partial b}$ 。

• 遍历每个训练样例，并计算：

  • 模型对该样例的预测值
    $$f_{wb}(x^{(i)})=w{x}^{(i)}+b$$

  • 参数w, b 相对于该样例的梯度
    $${\frac{\partial J(w,b)}{\partial b}}^{(i)}=(f_{w,b}(x^{(i)})-y^{(i)})$$
    $${\frac{\partial J(w,b)}{\partial w}}^{(i)}=(f_{w,b}(x^{(i)})-y^{(i)})x^{(i)}$$

• 返回所有样例的总梯度更新
  $$\frac{\partial J(w,b)}{\partial b}=\frac{1}{m}\sum _{i=0}^{m-1}{\frac{\partial J(w,b)}{\partial b}}^{(i)}$$

  $$\frac{\partial J(w,b)}{\partial w}=\frac{1}{m}\sum _{i=0}^{m-1}{\frac{\partial J(w,b)}{\partial w}}^{(i)}$$

  • 这里，$m$是训练样例的数量，$\sum$是求和操作符

如果您遇到困难，可以查看下面单元格中提供的提示来帮助您实现。

def coumpute_gradient(x,y,w,b):
    m = x.shape[0]
    dj_dw = 0
    dj_db = 0
    for i in range(m):
        f_wb = w*x[i]+b
        dj_dw += (f_wb-y[i])*x[i]
        dj_db += f_wb-y[i]
    return dj_dw/m,dj_db/m

批量梯度下降法学习参数

现在，您将使用批量梯度下降法找到线性回归模型的最优参数。批量指运行一次迭代中的所有示例。

• 对于此部分，您无需实现任何内容。只需运行下面的单元格即可。

• 验证梯度下降法是否正常工作的好方法是查看 $J(w,b)$ 的值并检查它是否随着每个步骤而减小。

• 假设您已经实现了梯度并正确计算了成本，并且您有合适的学习率 alpha，$J(w,b)$ 不应增加，并且应该在算法结束时收敛到稳定值。

def gradient_descent(x,y,w_in,b_in,cost_function,gradient_function,alpha,num):
    m = x.shape[0]
    J_history = []
    w_history = []
    w = copy.deepcopy(w_in)
    b = b_in
    for i in range(num):
        dj_dw,wj_db = gradient_function(x,y,w,b)
        w -= alpha*dj_dw
        b -= alpha*wj_db

        cost = cost_function(x,y,w,b)
        J_history.append(cost)
        w_history.append(w)
    return w,b,J_history,w_history

现在让我们运行上面的梯度下降算法来得出数据集的参数。

init_w = 0
inti_b = 0

number = 10000
alpha = 0.02

w,b,J_history,w_history = gradient_descent(x_train,y_train,init_w,inti_b,compute_cost,coumpute_gradient,alpha,number)
print(f"w:{w},b:{b}")

w:1.1930336441895875,b:-3.8957808783117933

fig,ax = plt.subplots(1,2,figsize=(20,8))
iterations = [j for j in range(number)]
ax[0].plot(iterations,J_history)
ax[0].set_title("J_history vs. ites")
ax[0].set_ylabel("J_history")
ax[0].set_xlabel("iterations")
ax[1].plot(iterations,w_history)
ax[1].set_title("w_history vs. iterations")
ax[1].set_ylabel("w_history")
ax[1].set_xlabel("iterations")

Text(0.5, 0, 'iterations')

​

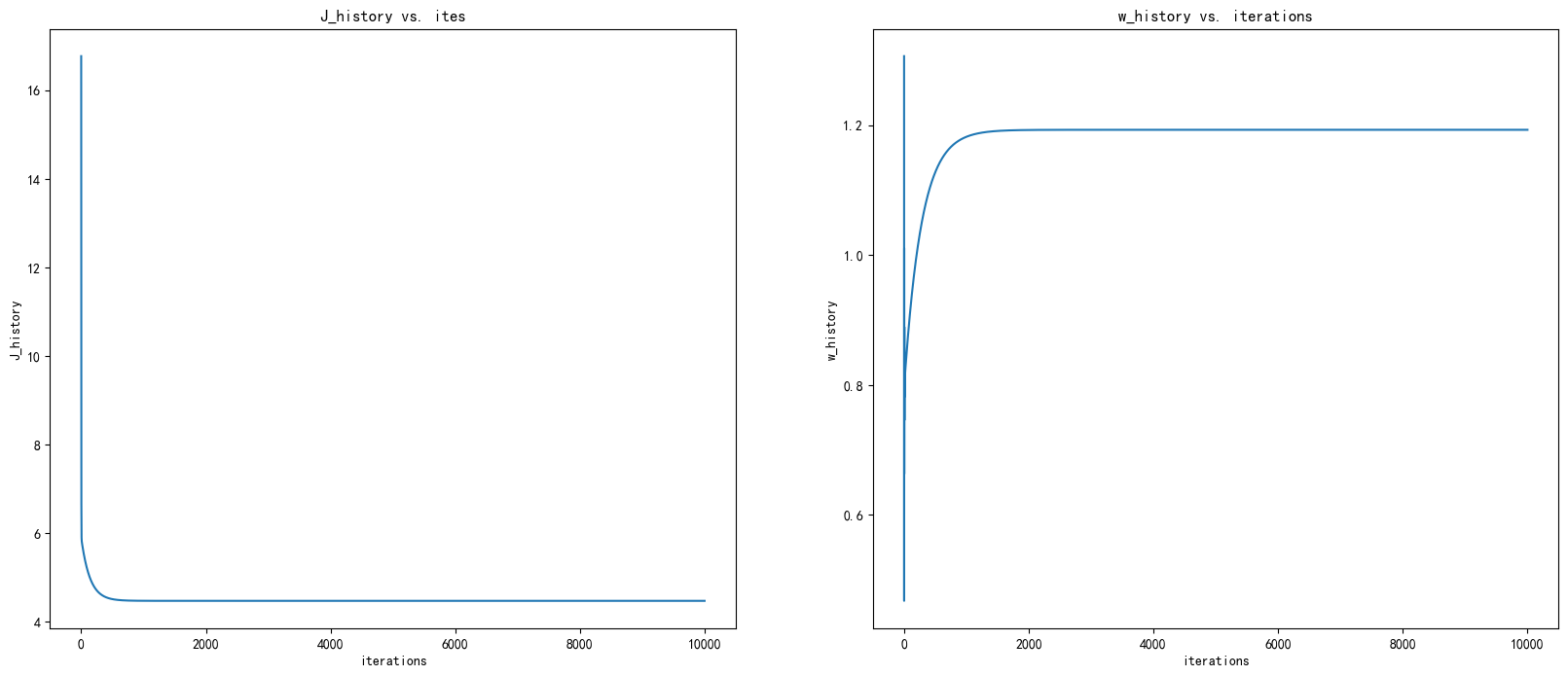
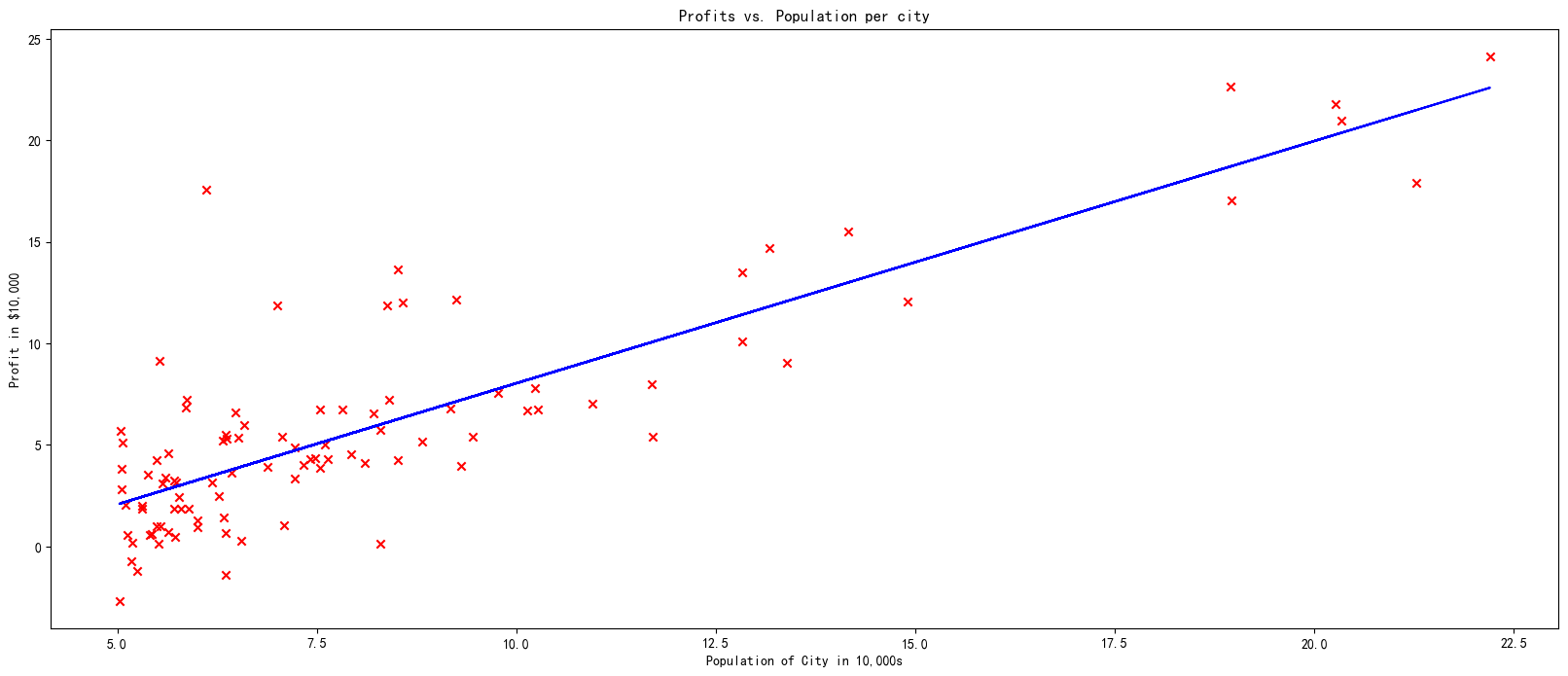
我们现在将使用梯度下降的最终参数来绘制线性拟合图。

回想一下，我们可以得到单个样本的预测值 $f(x^{(i)})=w{x}^{(i)}+b$。

为了计算整个数据集上的预测值，我们可以循环遍历所有训练样本，并计算每个样本的预测值。以下代码块展示了这一过程。

m = x_train.shape[0]
predicted = np.zeros(m)

for i in range(m):
    predicted[i] = w * x_train[i] + b

绘制拟合曲线

fig = plt.figure(figsize=(20,8))
plt.plot(x_train, predicted, c = "b")
plt.scatter(x_train, y_train, marker='x', c='r')
plt.title("Profits vs. Population per city")
plt.ylabel('Profit in $10,000')
plt.xlabel('Population of City in 10,000s')

Text(0.5, 0, 'Population of City in 10,000s')

​

​