算法模板(8):网络流(1):最大流
网络流基本概念
-
基本概念
- 流网络,不考虑反向边
- 可行流,不考虑反向边
- 两个条件(根据《算法导论》,这两个条件可以看作可行流的充要条件):容量限制( 0 ≤ f ( u , v ) ≤ C ( u , v ) 0 \le f(u,v) \le C(u,v) 0≤f(u,v)≤C(u,v),流量守恒(除了源点和汇点,每个节点的流入和流出相等)
- 可行流的流量:从源点流出的流量 - 流入源点的流量(多数时候为流入源点的流量为0)
- 最大流是指最大可行流
- 残留网络(一个可行流对应一个残留网络)
- 原网络里面,不需要考虑反向边;只有在残留网络里面才考虑反向边
- 考虑反向边,残留网络的可行流 f’ + 原图的可行流f = 原流网络的另一个可行流
(1) |f’ + f| = |f’| + |f|(这个加号的意思是,如果原图和新图的边的方向相同,那么就把新图的边的流量加上原图中;如果方向相反,就把原图中的边的流量)
(2) |f’| 可能是负数 - 残留网络的点集和原流网络的点集相等,边集分为两部分
- 正向边:容量定义为 c ′ ( u , v ) = c ( u , v ) − f ( u , v ) c'(u,v) = c(u,v)-f(u,v) c′(u,v)=c(u,v)−f(u,v)
- 反向边:容量定义为 c ′ ( u , v ) = f ( v , u ) c'(u,v)=f(v,u) c′(u,v)=f(v,u). (原图中的边是 v → u v \rightarrow u v→u)
- 当 ∣ f ′ ∣ = 0 |f'| = 0 ∣f′∣=0 时,现在的可行流不一定是最大流。不过当前可行流是最大流的时候, ∣ f ′ ∣ |f'| ∣f′∣ 必然是0
%ef%bc%9a网络流(1)%ef%bc%9a最大流.assets/image-20210518223732735.png)
- 增广路径:在残留网络里面,从源点出发,沿着大于0的边走,如果能走到汇点的话,那么该路径就是一条增广路径。如果残留网络不存在增广路的话,那么流网络当前的可行流一定是最大流。
- 割
- 割的定义:把点集划分成两个子集,并且保证源点和汇点分别属于两个子集。需要注意的是,子集中的点允许不连通.
- 割的容量:就是横跨两个集合,从
S
S
S 到
T
T
T 的边的容量之和
c
(
s
,
t
)
=
∑
u
∈
S
∑
v
∈
T
c
(
u
,
v
)
c(s,t) = \sum\limits_{u\in S}\sum\limits_{v \in T}c(u,v)
c(s,t)=u∈S∑v∈T∑c(u,v).
- 不考虑反向边,“最小割”是指容量最小的割。
- 割的流量:
f
(
s
,
t
)
=
∑
u
∈
S
∑
v
∈
T
f
(
u
,
v
)
−
∑
u
∈
T
∑
v
∈
S
f
(
u
,
v
)
f(s,t) = \sum\limits_{u\in S}\sum\limits_{v \in T}f(u,v) - \sum\limits_{u\in T}\sum\limits_{v \in S}f(u,v)
f(s,t)=u∈S∑v∈T∑f(u,v)−u∈T∑v∈S∑f(u,v)
- 考虑反向边, f ( S , T ) < = c ( S , T ) f(S, T) <= c(S, T) f(S,T)<=c(S,T)
- 性质,对于任意两个集合
X
,
Y
X, Y
X,Y
- f ( X , Y ) = ∑ u ∈ X ∑ v ∈ Y f ( u , v ) − ∑ u ∈ X ∑ v ∈ Y f ( v , u ) f(X,Y) = \sum\limits_{u \in X}\sum\limits_{v \in Y}f(u,v) - \sum\limits_{u \in X}\sum\limits_{v \in Y}f(v,u) f(X,Y)=u∈X∑v∈Y∑f(u,v)−u∈X∑v∈Y∑f(v,u)
- f ( X , Y ) = − f ( Y , X ) f(X,Y) = -f(Y, X) f(X,Y)=−f(Y,X)
- f ( Z , X ∪ Y ) = f ( Z , X ) + f ( Z , Y ) f(Z,X\cup Y) = f(Z, X) + f(Z,Y) f(Z,X∪Y)=f(Z,X)+f(Z,Y),其中 X ∩ Y = ∅ X \cap Y = \empty X∩Y=∅
- f ( X , X ) = 0 f(X,X) = 0 f(X,X)=0
- f ( X ∪ Y , Z ) = f ( X , Z ) + f ( Y , Z ) f(X\cup Y,Z) = f(X, Z) + f(Y,Z) f(X∪Y,Z)=f(X,Z)+f(Y,Z),其中 X ∩ Y = ∅ X \cap Y = \empty X∩Y=∅
- 对于任意可行流f,任意割 [ S , T ] [S, T] [S,T], ∣ f ∣ = f ( S , T ) |f| = f(S, T) ∣f∣=f(S,T)
- 对于任意可行流f,任意割 [ S , T ] [S, T] [S,T], ∣ f ∣ < = c ( S , T ) |f| <= c(S, T) ∣f∣<=c(S,T)
- 最大流最小割定理(三个条件相互等价)
- 可行流f是最大流
- 可行流f的残留网络中不存在增广路
- 存在某个割
[
S
,
T
]
[S, T]
[S,T],
∣
f
∣
=
c
(
S
,
T
)
|f| = c(S, T)
∣f∣=c(S,T)
- 由1推2:利用 ∣ f + f ′ ∣ = ∣ f ∣ + ∣ f ′ ∣ |f + f'| = |f| + |f'| ∣f+f′∣=∣f∣+∣f′∣ 反证
- 由2推3:若没有增广路,我们在残留网络中,令 S S S 是从源点出发直走大于 0 的边,能够走到的所有的点集; T T T 就是剩下的点组成的点集。由此可知:我们可以构造一个割出来,对于从 S S S 到 T T T 的边 u → v u \rightarrow v u→v,我们可以让 f ( u , v ) = c ( u , v ) f(u,v) = c(u,v) f(u,v)=c(u,v). 对于从 T T T 到 S S S 的边 u → v u\rightarrow v u→v,我们可以令 f ( u , v ) = 0 f(u,v) = 0 f(u,v)=0.。而 ∣ f ∣ = f ( S , T ) = ∑ u ∈ S ∑ v ∈ T f ( u , v ) − ∑ u ∈ T ∑ v ∈ S f ( u , v ) = ∑ u ∈ S ∑ v ∈ S c ( u , v ) = c ( S , T ) . |f| = f(S, T) = \sum\limits_{u\in S}\sum\limits_{v \in T}f(u,v) - \sum\limits_{u\in T}\sum\limits_{v \in S}f(u,v) = \sum\limits_{u\in S}\sum\limits_{v\in S}c(u,v) = c(S,T). ∣f∣=f(S,T)=u∈S∑v∈T∑f(u,v)−u∈T∑v∈S∑f(u,v)=u∈S∑v∈S∑c(u,v)=c(S,T).
- 由3推1:已证 f ( S , T ) = ∣ f ∣ ≤ c ( S , T ) f(S,T) = |f| \le c(S,T) f(S,T)=∣f∣≤c(S,T),即 最大流 ≤ 最小割 最大流 \le 最小割 最大流≤最小割。而 最大流 ≥ ∣ f ∣ = c ( S , T ) 最大流 \ge |f| = c(S,T) 最大流≥∣f∣=c(S,T)(某一个割的容量)。由此说明 最大流 ≥ 最小割 最大流 \ge 最小割 最大流≥最小割。因此最大流等于最小割。
- 算法
- EK O ( n m 2 ) O(nm^2) O(nm2)
- Dinic O ( n 2 m ) O(n^2m) O(n2m)
- 网络流的时间复杂度的上界是很宽松的,实际上多数达不到。
- 应用
- 二分图
- 二分图匹配
- 二分图多重匹配
- 上下界网络流
- 无源汇上下界可行流
- 有源汇上下界最大流
- 有源汇上下界最小流
- 多源汇最大流
- 二分图
最大流之算法模板
2171. EK求最大流
- 给定一个包含 n n n 个点 m m m 条边的有向图,并给定每条边的容量,边的容量非负。图中可能存在重边和自环。求从点 S S S 到点 T T T 的最大流 ( n ≤ 1000 , m ≤ 10000 , 0 ≤ m ≤ 100000 , S ≠ T n \le 1000,m \le 10000, 0 \le m \le 100000,S \ne T n≤1000,m≤10000,0≤m≤100000,S=T)
#include<bits/stdc++.h>
using namespace std;
const int N = 1010, M = 20010, INF = 1e8;
int n, m, S, T;
int h[N], f[M], e[M], ne[M], idx;
//d 到当前节点的最小流量,pre 存从哪个边转移过来.
int q[N], d[N], pre[N];
bool st[N];
void add(int a, int b, int c)
{
e[idx] = b, ne[idx] = h[a], f[idx] = c, h[a] = idx++;
e[idx] = a, ne[idx] = h[b], f[idx] = 0, h[b] = idx++;
}
bool bfs()
{
int hh = 0, tt = 0;
memset(st, false, sizeof st);
q[0] = S, st[S] = true, d[S] = INF;
while(hh <= tt){
int u = q[hh++];
for(int i = h[u]; i != -1; i = ne[i]){
int v = e[i];
if(st[v] || f[i] == 0) continue;
st[v] = true;
d[v] = min(d[u], f[i]);
pre[v] = i;
if(v == T) return true;
q[++tt] = v;
}
}
return false;
}
int EK()
{
int res = 0;
while(bfs()){
res += d[T];
for(int i = T; i != S; i = e[pre[i] ^ 1]){
f[pre[i]] -= d[T], f[pre[i] ^ 1] += d[T];
}
}
return res;
}
int main()
{
scanf("%d%d%d%d", &n, &m, &S, &T);
memset(h, -1, sizeof h);
while(m--){
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
add(a, b, c);
}
printf("%d\n", EK());
return 0;
}
2172. Dinic/ISAP求最大流
- 给定一个包含 n n n 个点 m m m 条边的有向图,并给定每条边的容量,边的容量非负。图中可能存在重边和自环。求从点 S S S 到点 T T T 的最大流 ( n ≤ 10000 , m ≤ 100000 , 0 ≤ c ≤ 10000 , S ≠ T n \le 10000, m \le 100000, 0 \le c \le 10000,S \ne T n≤10000,m≤100000,0≤c≤10000,S=T)
- Dinic 算法的优化的地方在于,建立一个分层图(防止环),把能够增广的地方全部增广;第二个优化是当前弧优化,相当于优先“榨干”一条边,“榨干”这条边后再“榨干”下一条边。
#include<bits/stdc++.h>
using namespace std;
const int N = 10100, M = 200010, INF = 1e8;
int n, m, S, T;
int h[N], f[M], e[M], ne[M], idx;
//d 到当前节点的最小流量,pre 存从哪个边转移过来.
int q[N], d[N], cur[N];
void add(int a, int b, int c)
{
e[idx] = b, ne[idx] = h[a], f[idx] = c, h[a] = idx++;
e[idx] = a, ne[idx] = h[b], f[idx] = 0, h[b] = idx++;
}
bool bfs()
{
//按照所有点到原点的距离建立分层图,并且更新当前弧(即优先榨取的边)
memset(d, -1, sizeof d);
int hh = 0, tt = 0;
q[0] = S, d[S] = 0, cur[S] = h[S];
while(hh <= tt){
int u = q[hh++];
for(int i = h[u]; i != -1; i = ne[i])
{
int v = e[i];
if(d[v] == -1 && f[i])
{
d[v] = d[u] + 1;
cur[v] = h[v];
if(v == T) return true;
q[++tt] = v;
}
}
}
return false;
}
int find(int u, int limit)
{
if(u == T) return limit;
int flow = 0;
for(int i = cur[u]; i != -1 && flow < limit; i = ne[i])
{
cur[u] = i; //当前弧优化
int v = e[i];
if(d[v] == d[u] + 1 && f[i])
{
int t = find(v, min(f[i], limit - flow));
if(!t) d[v] = -1;
f[i] -= t, f[i ^ 1] += t, flow += t;
}
}
return flow;
}
int dinic()
{
int res = 0, flow;
while(bfs()) while(flow = find(S, INF)) res += flow;
return res;
}
int main()
{
scanf("%d%d%d%d", &n, &m, &S, &T);
memset(h, -1, sizeof h);
while(m--)
{
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
add(a, b, c);
}
printf("%d\n", dinic());
return 0;
}
最大流之二分图匹配
2175. 飞行员配对方案问题 - AcWing题库
- 题意:第 1 1 1 行有 2 2 2 个正整数 m m m 和 n n n。 m m m 是外籍飞行员数; n n n 是皇家空军的飞行员总数。外籍飞行员编号为 1 ∼ m 1∼m 1∼m;英国飞行员编号为 m + 1 ∼ n m+1∼n m+1∼n。接下来每行有 2 2 2 个正整数 i i i 和 j j j,表示外籍飞行员 i i i 可以和英国飞行员 j j j 配合。文件最后以 2 2 2 个 − 1 −1 −1 结束。问最大匹配数以及匹配方案。
- 一个问题和一个网络流问题等价,意味着问题的解集与可行流集合是一一对应的。一个流是否是可行流,判断:(1)流量是否守恒;(2)是否超出容量。
- 用 D i n i c Dinic Dinic 算法求二分匹配最大数,复杂度是 O ( m n ) O(m\sqrt n) O(mn).
#include<bits/stdc++.h>
using namespace std;
const int N = 110, M = 5210, INF = 1e8;
int h[N], e[M], ne[M], f[M], idx;
int q[N], cur[N], d[N];
int n, m, S, T;
//略去 dinic 的模板,只保留建图模板.
int main()
{
memset(h, -1, sizeof h);
scanf("%d%d", &m, &n);
S = n + 1, T = n + 2;
int a, b;
while(cin >> a >> b, a != -1)
{
add(a, b, 1);
}
for(int i = 1; i <= m; i++) add(S, i, 1);
for(int i = m + 1; i <= n; i++) add(i, T, 1);
printf("%d\n", dinic());
for(int i = 0; e[i ^ 1] != S; i += 2)
{
if(f[i] == 0) printf("%d %d\n", e[i ^ 1], e[i]);
}
}
2179. 圆桌问题 - AcWing题库
-
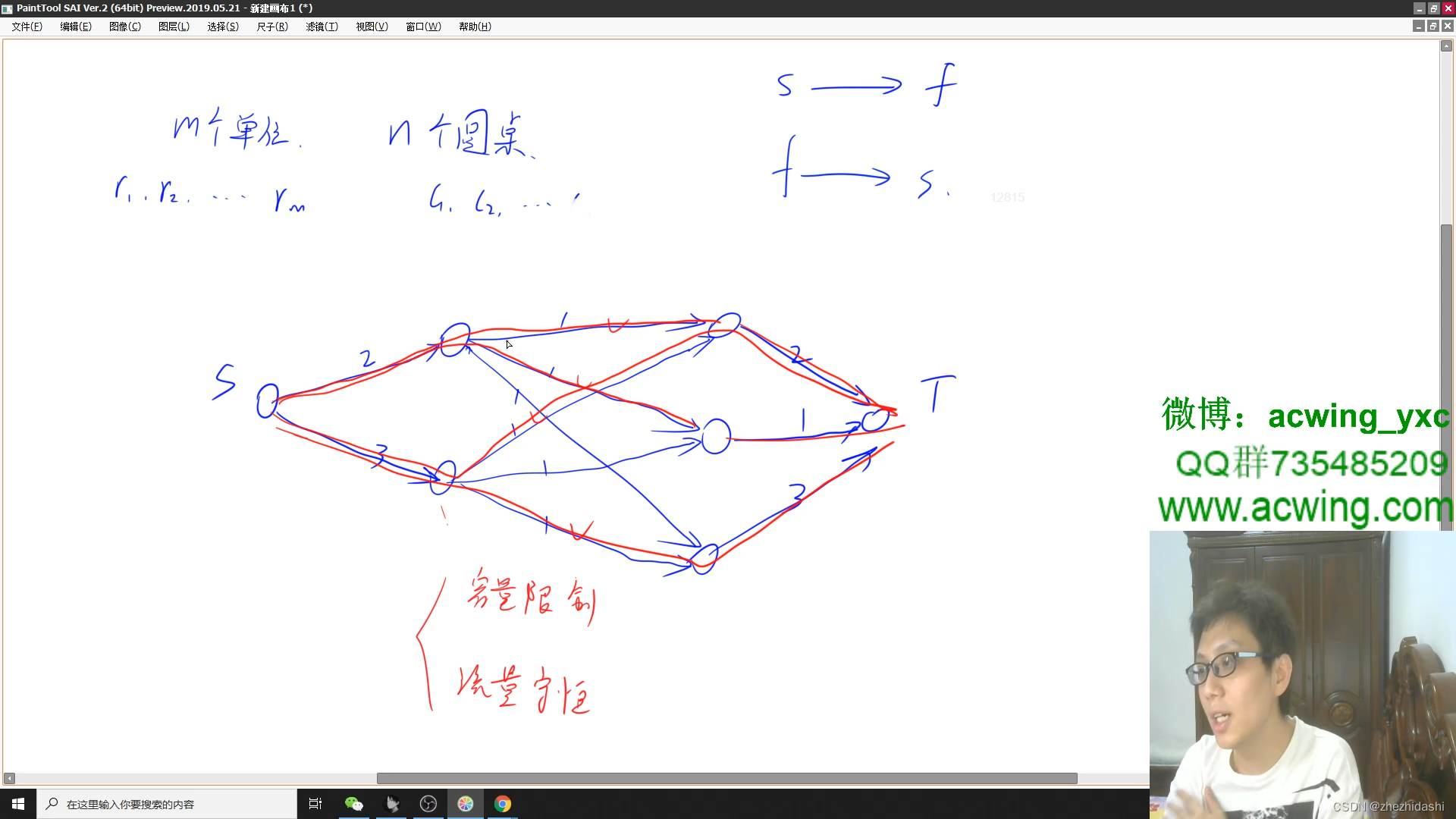
题意:假设有来自 m m m 个不同单位的代表参加一次国际会议。每个单位的代表数分别为 r i ( i = 1 , 2 , … , m ) r_i(i=1,2,\dots,m) ri(i=1,2,…,m)。会议餐厅共有 n n n 张餐桌,每张餐桌可容纳 c i ( i = 1 , 2 , … , n ) c_i(i=1,2,\dots,n) ci(i=1,2,…,n) 个代表就餐。为了使代表们充分交流,希望从同一个单位来的代表不在同一个餐桌就餐。试设计一个算法,给出满足要求的代表就餐方案。
-
二分图的多重匹配问题,构造一个二分图,源点连向左半部分的图,边的容量是点权;右半部分的图向汇点连边,容量也是点权;左右两部分的结点两两相连,容量为1.
// 省去 dinic 模板部分,只保留建图
int main()
{
memset(h, -1, sizeof h);
scanf("%d%d", &m, &n);
S = 0, T = n + m + 1;
int tot = 0;
for(int i = 1; i <= m; i++)
{
int r;
scanf("%d", &r);
tot += r;
add(S, i, r);
}
for(int i = m + 1; i <= m + n; i++)
{
int c;
scanf("%d", &c);
add(i, T, c);
}
for(int i = 1; i <= m; i++)
{
for(int j = 1; j <= n; j++)
{
add(i, j + m, 1);
}
}
int res = dinic();
if(res != tot) printf("0\n");
else
{
printf("1\n");
for(int u = 1; u <= m; u++)
{
for(int i = h[u]; i != -1; i = ne[i])
{
if(m + 1 <= e[i] && e[i] <= m + n && !f[i])
{
printf("%d ", e[i] - m);
}
}
printf("\n");
}
}
return 0;
}
最大流之上下界可行流
2188. 无源汇上下界可行流 - AcWing题库
- 给定一个包含 n n n 个点 m m m 条边的有向图,每条边都有一个流量下界和流量上界。求一种可行方案使得在所有点满足流量平衡条件的前提下,所有边满足流量限制。
- 建图方式,每条边都减去容量下界;对于每个点,计算容量下界入度之和 C i n C_{in} Cin 和下界出度之和 C o u t C_{out} Cout,若 C i n > C o u t C_{in} > C_{out} Cin>Cout,那么从源点 S S S 到该点连一条容量为 C i n − C o u t C_{in} - C_{out} Cin−Cout 的边。因为在新图中如果不加这样的边,流量可能不守恒,减去的入流比减去的出流要多,那么把这个多减掉的东西补上去。同理,如果 C i n < C o u t C_{in} < C_{out} Cin<Cout,那么就是从当前结点向汇点连一条 C o u t − C i n C_{out} - C_{in} Cout−Cin 的边.
- 当然需要满足从 S S S 发出的边需要满流,不然不满足流量守恒;同理需要满足到汇点 T T T 需要满流。不过原图中每一条边都会贡献一个入度和出度。因此在新图中, S S S 发出的边的容量一定等于汇入 T T T 的容量,加上从源点流出的流量一定等于流入汇点的流量。因此只要一个满流,另一个一定会满流。
int main()
{
memset(h, -1, sizeof h);
scanf("%d%d", &n, &m);
S = 0, T = n + 1;
for(int i = 1; i <= m; i++)
{
int a, b, c, d;
scanf("%d%d%d%d", &a, &b, &c, &d);
add(a, b, c, d);
A[a] -= c, A[b] += c;
}
int tot = 0;
for(int i = 1; i <= n; i++)
{
if(A[i] > 0) add(S, i, 0, A[i]), tot += A[i];
else if(A[i] < 0) add(i, T, 0, -A[i]);
}
if(dinic() != tot) printf("NO\n");
else
{
printf("YES\n");
for(int i = 0; i < 2 * m; i += 2)
{
//注意流量要输出反向边
printf("%d\n", f[i ^ 1] + l[i]);
}
}
return 0;
}
2189. 有源汇上下界最大流 - AcWing题库
- 题意:给定一个包含 n n n 个点 m m m 条边的有向图,每条边都有一个流量下界和流量上界。给定源点 S S S 和汇点 T T T,求源点到汇点的最大流。
- 另一种建图方式如下,对于每个点 v v v,建一条从 S S S 到 v v v 容量是入度下界之和的边,以及一条从 v v v 指向 T T T 容量出度下界之和。然后从 原图的 t t t 到 s s s 的一条容量为 ∞ \infty ∞ 的边,这样子可以保证所有点的流量守恒
- 原图的任意一个可行流,都对应于新图任意一个最大流?证明没懂
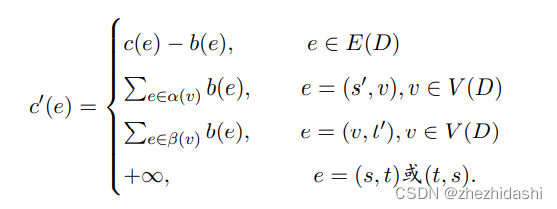
2190. 有源汇上下界最小流 - AcWing题库
- 题意:给定一个包含 n n n 个点 m m m 条边的有向图,每条边都有一个流量下界和流量上界。给定源点 S S S 和汇点 T T T,求源点到汇点的最小流。