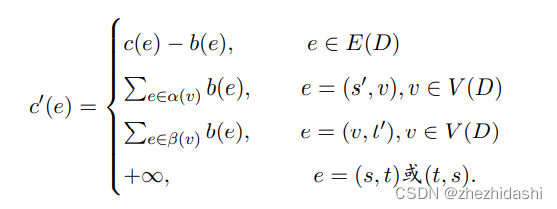Eppstein的算法是David Eppstein于1998年提出的一种高效且易于实现的k条最短路径寻找方法。它的时间复杂度为O(m + n log n + k),其中m是边的数量,n是节点的数量,k是要寻找的路径数。相较于其他方法,它具有较好的性能和实用性。
Eppstein algorithm的关键步骤
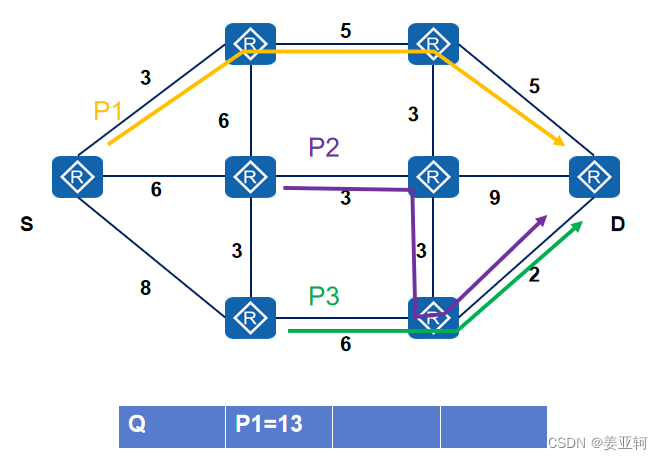
1.对于给定的图G(V, E),构造所有节点到目标节点D的最短路径树。
2.初始化一个优先级队列Q,将源节点S到目标节点D的最短路径P1放入队列Q。
3.对于每一条边(u, v),计算其对应的sidetrack边(u, v)。这里,sidetrack边(u, v)表示使用边(u, v)替换从u到目标节点D的路径上的某个边所带来的权重变化。delta(u, v) = w(u, v) - w(T(u)) + w(T(v)),其中w(u, v)表示边(u, v)的权重,w(T(u))表示从u到目标节点D在最短路径P1中的路径的权重,w(T(v))表示从v到目标节点D在最短路径P1中的路径的权重。
4.重复以下步骤K-1次,以找到K条最短路径:
- 从优先级队列Q中取出权重最小的路径P。
- 将路径P加入到最短路径列表中。
- 对于路径P上的每个顶点v,找到sidetrack边(u, v)并计算新路径。将从源节点S到顶点u的路径P(u)与边(u,v)以及从顶点v到目标节点D的路径P’(v)连接起来,形成一条新路径P’。将新路径P’加入到优先级队列Q中。
5.返回找到的K条最短路径。
Eppstein algorithm图例
1和2.构造所有节点到目标节点D的最短路径树,并将源节点S到目标节点D的最短路径P1放入队列Q,我这里两步并为一步了
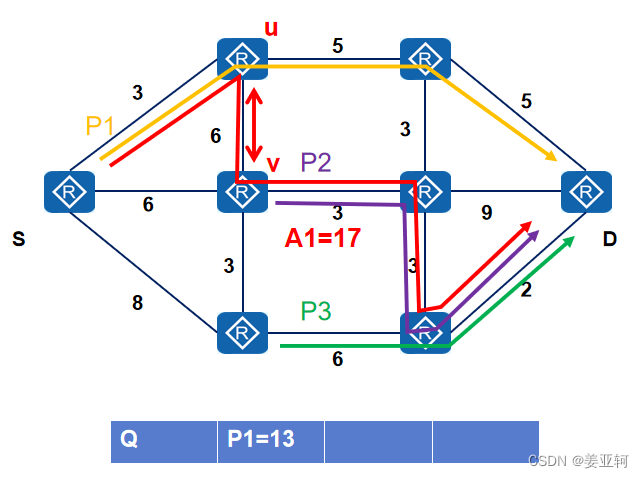
3.假设图示的两个节点为u和v, 计算sidetrack边(u, v)所带来的权重变化:
delta(u,v)= w(u,v)-W(T(u))+W(T(v))= 6 - 10 + 8 = 4
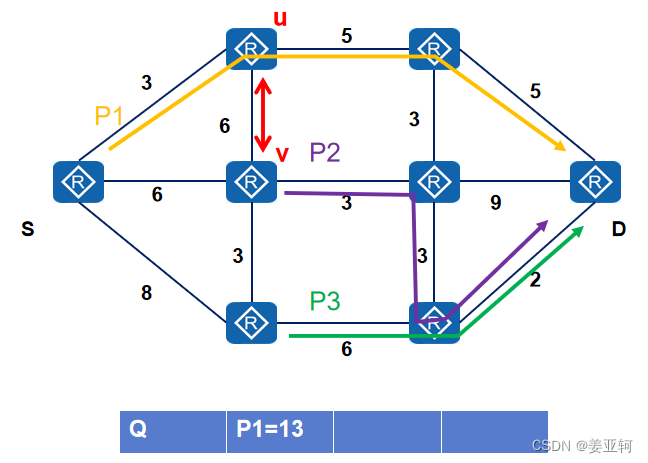
所谓的权重变化,就是如果流量往sidetrack边(u, v)走的话,整条路径的权重变化
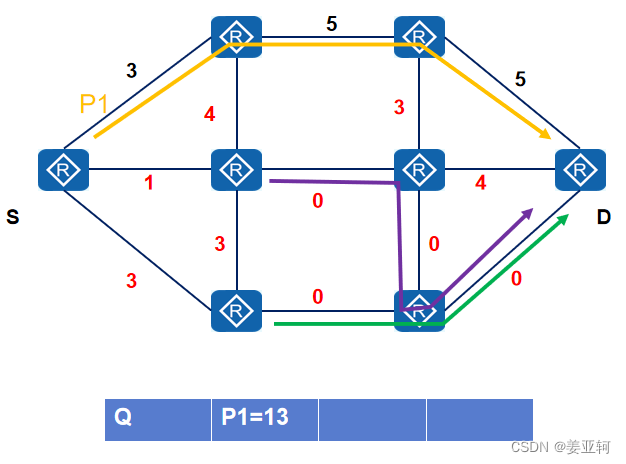
接着我们计算所有sidetrack边的权重变化值,将链路的weight改为权重变化值,如下图所示,注意,处在最小路径树上的边权重变化为0
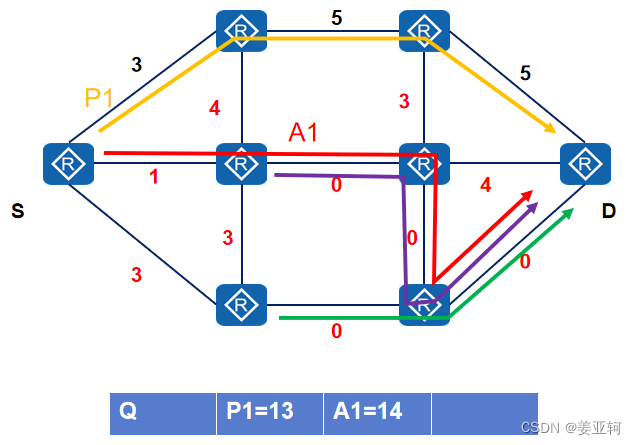
这样就计算出来第二段的路径A1=13+1=14,如下图,如果K=2的话那结果就是P1和A1
如果K>2的话,将A1加入到Q队列后,A1也成为最短路径树的一部分,此时的sidetrack边(u, v)变成除了P1和A1以外的边,再次重新计算所有sidetrack边(u, v)所带来的权重变化(可能会变化),并通过计算得到A2等
总体体验下来,Eppstein的算法确实较于Yen的算法改进了不少,尤其是时间复杂度方面,而且算法本身也更加灵活