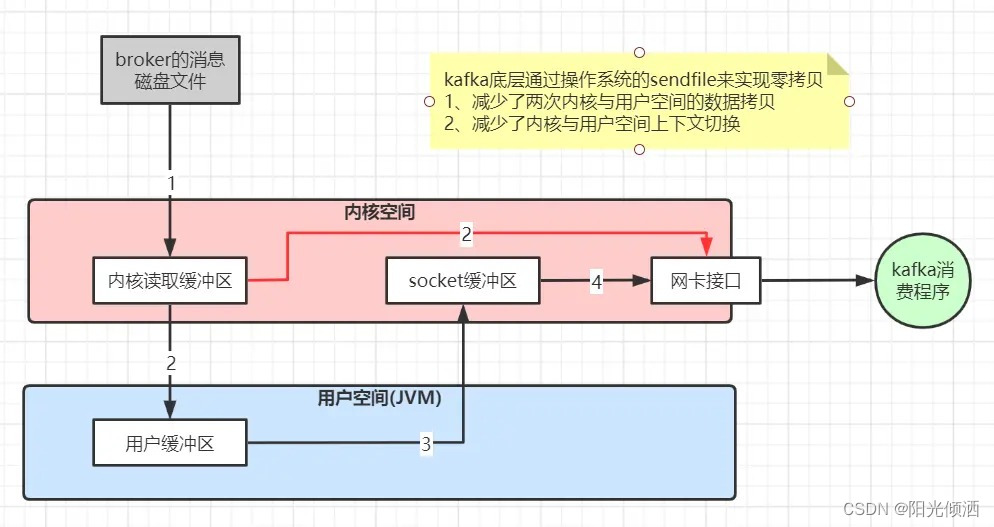
1.因子分析

1.1 探索性因子分析

探索性因子分析（Exploratory Factor Analysis，EFA）是一种统计方法，用于分析观测变量之间的潜在结构和关联性。它旨在确定多个观测变量是否可以归结为较少数量的潜在因子，从而帮助简化数据集和提取隐藏的信息。

在探索性因子分析中，我们收集一组观测变量的数据，并试图找到解释这些变量之间关系的较少数量的潜在因子。这些潜在因子是无法直接观测到的，但它们可以通过变量之间的共同方差来解释观测数据的模式。

探索性因子分析的主要目标是确定以下内容：

1. 因子结构：通过观察变量之间的共同变异性，确定潜在因子的数量和性质。
2. 因子载荷：衡量每个变量与每个因子之间的关系强度。较高的因子载荷表示变量与因子之间存在较强的关联。
3. 因子解释：解释每个因子所代表的潜在构念或概念。这可以通过变量与因子之间的关系和变量的解释程度来实现。

探索性因子分析可以用于数据降维、构建测量工具、发现潜在因素和进行模型建立等领域。它被广泛应用于社会科学、心理学、教育、市场研究等领域，以揭示变量之间的潜在结构和解释现象背后的因素。

主成分分析：

主成分分析是一种降维技术，它旨在将高维数据转化为较低维度的表示，同时尽可能保留原始数据的信息。主成分分析通过线性变换将原始变量转化为一组互相无关的主成分，其中每个主成分都是原始变量的线性组合。这些主成分按照其解释的方差大小排序，通常只保留方差较大的主成分。

在探索性因子分析中，主成分分析被用于确定潜在因子的数量和性质。它通过计算每个主成分的方差贡献和特征载荷（变量与主成分之间的相关系数）来帮助解释原始变量之间的相关性和共同性。主成分分析可以帮助识别潜在因子，并提供每个变量对于每个主成分的贡献程度。

主成分分析的步骤通常包括以下内容：

1. 数据准备：收集相关变量的观测数据，并进行数据清洗和预处理。
2. 计算协方差矩阵或相关系数矩阵：根据数据的特点，计算变量之间的协方差矩阵或相关系数矩阵。
3. 提取主成分：使用特征值分解或奇异值分解等方法，计算协方差矩阵的特征值和特征向量，从中提取主成分。
4. 解释方差贡献：计算每个主成分的方差贡献，并确定保留的主成分数量。
5. 解释主成分：通过观察主成分与原始变量之间的特征载荷，解释每个主成分所代表的意义和含义。
6. 结果解释：根据主成分的解释和方差贡献，解释原始变量之间的相关性和共同性，推断潜在因子结构。

主成分分析在数据降维、变量选择、特征提取等领域有广泛应用。它可以帮助简化复杂的数据集，减少变量的数量，并提供变量之间的结构信息。主成分分析在数据预处理、数据挖掘、模式识别等领域中发挥着重要作用，为后续分析和解释提供

1.2 验证性因子分析

验证性因子分析（Confirmatory Factor Analysis，CFA）是一种结构方程模型的方法，用于验证已经提出的潜在因子结构模型是否与观测数据相符。

在验证性因子分析中，研究者根据理论或先前的研究假设一个潜在因子结构模型，然后使用观测数据来评估该模型与实际数据的拟合程度。验证性因子分析的目标是确定潜在因子模型是否能够恰当地解释观测变量之间的关系，并提供有关模型拟合程度的统计指标。

在验证性因子分析中，常用的评估指标和统计方法包括：

1. 相关性（Correlation）：通过计算观测变量之间的相关系数，评估模型中潜在因子之间的关联程度。

2. 卡方检验（Chi-Square Test）：用于评估观测数据与模型之间的拟合程度。卡方检验比较观测数据与理论模型之间的差异，若差异较小，则说明模型与数据拟合较好。

3. 覆盖度（Coverage）：评估模型中的潜在因子是否能够覆盖观测变量的变异。覆盖度可以通过计算模型中潜在因子的方差贡献或占总变异的比例来衡量。

4. 方差分析（ANOVA）：用于评估模型中不同组别之间的差异程度。方差分析可以帮助检验潜在因子模型是否能够解释观测数据中的组别差异。

5. 熵（Entropy）：用于衡量模型中潜在因子的信息量和不确定性。熵越小表示模型解释观测数据的能力越强。

6. F-值（F-Value）：用于比较模型拟合指标在不同模型之间的差异。F-值可以帮助确定是否存在更好的模型来解释观测数据。

7. 自定义指标：根据研究者的需求，可以定义和使用其他适用的指标和统计方法来评估验证性因子分析模型的拟合程度和解释能力。

验证性因子分析是一种复杂的数据分析方法，需要具备统计学和结构方程模型的知识。在实际应用中，通常使用统计软件（如R、SPSS、AMOS等）来执行验证性因子分析，并根据评估指标进行模型拟合和解释。

2. 主成分分析实例

2.1 代碼

import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
from sklearn.decomposition import PCA #用于执行主成分分析。

sns.set_context(font_scale=1.5)
df = pd.read_csv("../data/HR.csv")

# 处理缺失值
df = df.dropna()  # 删除包含缺失值的行

my_pca = PCA(n_components=7)
lower_mat = my_pca.fit_transform(df.drop(labels=["salary", "department", "left"], axis=1))
print("Ratio:", my_pca.explained_variance_ratio_)

sns.heatmap(pd.DataFrame(lower_mat).corr(), vmin=-1, vmax=1, cmap=sns.color_palette("RdBu", n_colors=128))
plt.show()

1. 处理缺失值：

   • 使用dropna()函数删除包含缺失值的行，更新df。

2. 创建PCA对象my_pca，并设置要提取的主成分数量为7。

3. 使用fit_transform()方法对从df中删除 "salary"、"department" 和 "left" 列后的数据执行主成分分析。将结果存储在lower_mat中。

4. 打印主成分的解释方差比例，即每个主成分所解释的方差的比例。

5. 使用seaborn的heatmap()函数创建相关性热图，传入pd.DataFrame(lower_mat).corr()作为相关性矩阵，设置颜色映射为"RdBu"色板，并指定颜色范围。

6. 使用plt.show()显示绘制的热图。

总体而言，这段代码的目的是通过主成分分析对数据进行降维，并可视化主成分之间的相关性。它可以帮助我们理解数据的结构和特征之间的关系。

2.2 分析结果

Ratio: [9.98565312e-01 8.69277622e-04 4.73866604e-04 4.96913206e-05
 2.43160255e-05 9.29566680e-06 8.24092853e-06]

结果显示了主成分分析中每个主成分所解释的方差比例。具体来说，结果为：

• 第一个主成分解释了总方差的约99.86%。
• 第二个主成分解释了总方差的约0.09%。
• 第三个主成分解释了总方差的约0.05%。
• 第四个主成分解释了总方差的约0.005%。
• 第五个主成分解释了总方差的约0.002%。
• 第六个主成分解释了总方差的约0.001%。
• 第七个主成分解释了总方差的约0.001%。

这些方差比例表示了每个主成分对数据中的变异程度的贡献。第一个主成分的方差比例最大，说明它包含了最多的信息。随着主成分的编号递增，方差比例逐渐减小，表明后续的主成分解释的方差较小，包含的信息量也较少。

这些方差比例可用于确定选择多少个主成分以保留数据中的有效信息。通常，我们可以选择累计方差比例达到一定阈值（如90%或95%）的主成分作为降维后的特征。

2.3 效果热图

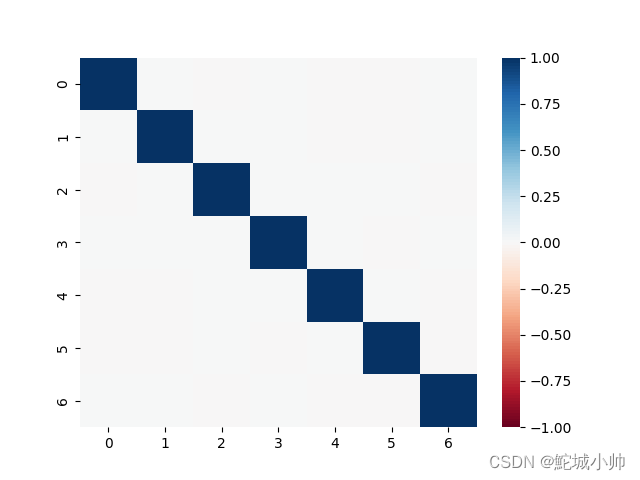
通过主成分分析热图可知，只有对角线上的相关系数几乎为1，其他区域几乎为零，几乎不相关。所以说，主成分分析把原来的特征空间变成了正交的特征空间。

主成分分析将原始特征空间转换为正交的特征空间。在转换后的特征空间中，主成分之间几乎没有相关性，即主成分之间的相关系数接近零，而主成分自身的相关系数接近1。

这种正交性意味着主成分是相互独立的，每个主成分捕捉到数据中的不同方差来源。第一个主成分解释了最大的方差，它是数据中变化最大的方向。随后的主成分依次解释了剩余的方差，并与之前的主成分正交。

因此，通过主成分分析，我们可以通过选择具有较高方差比例的主成分来减少特征的维度，并保留数据中最重要的信息。同时，正交的特征空间使得主成分之间彼此独立，降低了多重共线性的问题，更方便进行后续的统计分析和建模。

3. 小结

3.1 数据集类型与分析方法选择

数据类型	可用方法
连续---连续	相关系数、假设检验
连续---离散（二值）	相关系数，连续二值化（最小Gini切分，最大熵增益切分）
连续---离散（非二值）	相关系数（定序）
离散（二值）--- 离散（二值）	相关系数，熵相关，F分值
离散--- 离散（非二值）	熵相关，Gini，相关系数（定序）