引言
本文介绍概率图模型的部分基础知识,希望学习完本文之后能更好地理解HMM和CRF模型。
概率论基础
本节简单回顾一下相关的概率论知识,概率论有两条重要的基本规则。
分别为乘法规则(product rule)和加和规则(sum rule),假设有两个随机变量 X X X和 Y Y Y。
首先看乘积规则:
P
(
X
,
Y
)
=
P
(
Y
∣
X
)
P
(
X
)
(1)
P(X,Y) = P(Y|X)P(X) \tag 1
P(X,Y)=P(Y∣X)P(X)(1)
下面来看加和规则:
P
(
X
)
=
∑
Y
P
(
X
,
Y
)
(2)
P(X) = \sum_Y P(X,Y) \tag 2
P(X)=Y∑P(X,Y)(2)
这里
p
(
X
,
Y
)
p(X,Y)
p(X,Y)是联合概率,表示
X
X
X和
Y
Y
Y同时发生的概率;
P
(
Y
∣
X
)
P(Y|X)
P(Y∣X)是条件概率,给定
X
X
X的条件下
Y
Y
Y的概率;
P
(
X
)
P(X)
P(X)是边缘概率,它是通过把其他变量(
Y
Y
Y)边缘化或加和得到的。
式 ( 2 ) (2) (2)表明了边缘概率和联合概率的关系。
根据乘积规则和对称性
P
(
X
,
Y
)
=
P
(
Y
,
X
)
P(X,Y)=P(Y,X)
P(X,Y)=P(Y,X),有
P
(
Y
∣
X
)
P
(
X
)
=
P
(
X
∣
Y
)
P
(
Y
)
P(Y|X)P(X)=P(X|Y)P(Y)
P(Y∣X)P(X)=P(X∣Y)P(Y),稍作整理,我们就得到了这两个条件概率之间的关系:
P
(
Y
∣
X
)
=
P
(
X
∣
Y
)
P
(
Y
)
P
(
X
)
(3)
P(Y|X)= \frac{P(X|Y)P(Y)}{P(X)} \tag 3
P(Y∣X)=P(X)P(X∣Y)P(Y)(3)
上式就是著名的贝叶斯定理,所以根据就不用记,只要知道这两条基本规则,随时可以推导出来。
再基于加和规则,把上式中的分母用出现在分子中的项表示:
P
(
X
)
=
∑
Y
P
(
X
,
Y
)
=
∑
Y
P
(
X
∣
Y
)
P
(
Y
)
(4)
P(X) = \sum_Y P(X,Y) = \sum_Y P(X|Y)P(Y) \tag 4
P(X)=Y∑P(X,Y)=Y∑P(X∣Y)P(Y)(4)
代入到
(
3
)
(3)
(3)式中有:
P
(
Y
∣
X
)
=
P
(
X
∣
Y
)
P
(
Y
)
∑
Y
P
(
X
∣
Y
)
P
(
Y
)
(5)
P(Y|X)= \frac{P(X|Y)P(Y)}{\sum_Y P(X|Y)P(Y)} \tag 5
P(Y∣X)=∑YP(X∣Y)P(Y)P(X∣Y)P(Y)(5)
我们可以把这个分母看成是归一化常数,用来确保公式
(
5
)
(5)
(5)左侧的条件概率对于所有的
Y
Y
Y的取值之和为
1
1
1。
如果两个变量的联合分布可以分解为两个边缘分布的乘积,即
P
(
X
,
Y
)
=
P
(
X
)
P
(
Y
)
P(X,Y)=P(X)P(Y)
P(X,Y)=P(X)P(Y),那么
X
X
X和
Y
Y
Y相互独立。根据乘积规则,可以得到
P
(
Y
∣
X
)
=
P
(
Y
)
P(Y|X)=P(Y)
P(Y∣X)=P(Y):
P
(
X
,
Y
)
=
P
(
Y
∣
X
)
P
(
X
)
P
(
X
)
P
(
Y
)
=
P
(
Y
∣
X
)
P
(
X
)
P
(
Y
)
=
P
(
Y
∣
X
)
(6)
\begin{aligned} P(X,Y) &= P(Y|X)P(X) \\ P(X)P(Y) &= P(Y|X)P(X) \\ P(Y) &= P(Y|X) \end{aligned} \tag 6
P(X,Y)P(X)P(Y)P(Y)=P(Y∣X)P(X)=P(Y∣X)P(X)=P(Y∣X)(6)
即对于给定
X
X
X条件下的
Y
Y
Y的条件分布独立于
X
X
X的值。
概率图模型
概率图模型(probabilistic graphical models,PGMs)是概率分布的图形表示,它非常方便我们分析模型的性质,尤其是条件独立性质。
和我们数据结构中学的图一样,一个图由结点、结点间的边组成。概率图模型中,每个结点表示一个随机变量,边表示这些变量之间的概率关系,缺失的边表示这些变量间的条件独立(conditional independence,CI)假设。
概率图主要分为两大类:有向图模型,也称为贝叶斯网络(实际上和贝叶斯关系不大);无向图模型,也称为马尔可夫随机场(名字也没那么直观)。
有向图模型
本节主要简单介绍有向概率图模型(directed probabilistic graphical models,DPGM),也称为有向图模型。它基于有向无环图(directed acyclic graphs,DAGs)。
首先介绍下 条件独立(conditional independence, CI) 的概念。
我们先来回顾下独立的概念,假设有两个随机变量
a
,
b
a,b
a,b相互独立的话,有
p
(
a
,
b
)
=
p
(
a
)
p
(
b
)
p(a,b)= p(a)p(b)
p(a,b)=p(a)p(b)
如果此时求给定
b
b
b的条件下
a
a
a的概率:
p
(
a
∣
b
)
=
p
(
a
,
b
)
p
(
b
)
=
p
(
a
)
p
(
b
)
p
(
b
)
=
p
(
a
)
(7)
p(a|b) = \frac{p(a,b)}{p(b)} = \frac{p(a)p(b)}{p(b)} = p(a) \tag 7
p(a∣b)=p(b)p(a,b)=p(b)p(a)p(b)=p(a)(7)
即不管
b
b
b的取值如何,都不影响
a
a
a发生的概率。也可以说
a
a
a条件独立于
b
b
b。
现在假设有三个变量
a
,
b
,
c
a,b,c
a,b,c,假设给定
b
,
c
b,c
b,c的条件下
a
a
a的条件分布不依赖于
b
b
b的值,即
p
(
a
∣
b
,
c
)
=
p
(
a
∣
c
)
(8)
p(a|b,c) = p(a|c) \tag 8
p(a∣b,c)=p(a∣c)(8)
也就是说,在给定
c
c
c的条件下,
a
a
a条件独立于
b
b
b。在给定
c
c
c的条件下,
b
b
b作为条件的取值不会影响
p
(
a
∣
c
)
p(a|c)
p(a∣c)。
我们考虑将
p
(
a
,
b
∣
c
)
p(a,b|c)
p(a,b∣c)展开:
p
(
a
,
b
∣
c
)
=
p
(
a
∣
b
,
c
)
p
(
b
∣
c
)
=
p
(
a
∣
c
)
p
(
b
∣
c
)
(9)
p(a,b|c) = p(a|b,c)p(b|c) = p(a|c)p(b|c) \tag 9
p(a,b∣c)=p(a∣b,c)p(b∣c)=p(a∣c)p(b∣c)(9)
(
p
2
)
(p2)
(p2)和
(
p
3
)
(p3)
(p3)都是在这种情况下条件独立的不同描述。
注意条件独立中的条件二字,比如这里都是在以
c
c
c为条件的前提下,而且是对于
c
c
c的所有取值都成立。
记为
a
⊥
b
∣
c
(10)
a \,\bot \,b \,|\, c \tag{10}
a⊥b∣c(10)
表示给定
c
c
c的条件下
a
a
a和
v
v
v条件独立。
我们以此为基础再来看下马尔可夫链,假设 x t + 1 ⊥ x 1 : t − 1 ∣ x t x_{t+1} \,\bot \,x_{1:t-1} \, | \, x_t xt+1⊥x1:t−1∣xt,即下一时刻仅依赖于当前时刻,和所有的之前时刻无关,这就是(一阶)马尔可夫假设。
基于该假设,结合链式法则,
x
1
:
N
x_{1:N}
x1:N的联合概率分布可以写成:
p
(
x
1
:
N
)
=
p
(
x
1
)
∏
t
=
2
N
p
(
x
t
∣
x
1
:
t
−
1
)
=
p
(
x
1
)
∏
t
=
2
N
p
(
x
t
∣
x
t
−
1
)
(11)
p(x_{1:N})=p(x_1)\prod_{t=2}^N p(x_t|x_{1:t-1}) = p(x_1)\prod _{t=2}^N p(x_t|x_{t-1}) \tag{11}
p(x1:N)=p(x1)t=2∏Np(xt∣x1:t−1)=p(x1)t=2∏Np(xt∣xt−1)(11)
这就是一阶马尔可夫链。这里说的一阶是什么意思?说的
x
t
x_t
xt仅依赖于
x
t
−
1
x_{t-1}
xt−1,如果是二阶,则依赖于
x
t
−
1
,
x
t
−
2
x_{t-1},x_{t-2}
xt−1,xt−2。相当于假设要弱一点,但带来的复杂性也高一点。那最强的假设是什么,贝叶斯假设,所有的
x
t
x_t
xt之间是相互独立的。
前面说概率图模型是概率分布的图形表示,那么它如何表示概率分布呢?
考虑三个变量
a
,
b
,
c
a,b,c
a,b,c的联合分布
p
(
a
,
b
,
c
)
p(a,b,c)
p(a,b,c),此时我们不对这些变量做出任何的假设,通过概率的乘积规则,可以将联合概率分布写成:
p
(
a
,
b
,
c
)
=
p
(
c
∣
a
,
b
)
p
(
a
,
b
)
=
p
(
c
∣
a
,
b
)
p
(
b
∣
a
)
p
(
a
)
(12)
p(a,b,c)=p(c|a,b)p(a,b)=p(c|a,b)p(b|a)p(a) \tag{12}
p(a,b,c)=p(c∣a,b)p(a,b)=p(c∣a,b)p(b∣a)p(a)(12)
此时,我们引入图模型来表示上面等式的右侧,有向图模型的核心属性在于是有序的,这里保证的是父结点出现在子结点之前,这被称为拓扑排序(topological ordering)。
首先我们为每个随机变量引入一个结点,然后为每个结点关联上式右侧对应的条件概率,然后,对于每个条件概率分布,我们在图中添加一个链接(箭头),箭头的起点是条件概率中条件的随机变量对应的结点。结果就是图1中的图。
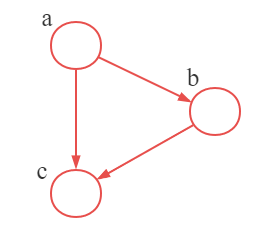
可以看到,这个图描述了联合概率分布
p
(
a
,
b
,
c
)
p(a,b,c)
p(a,b,c)在所有随机变量上能分解成一组因子的乘积的方式,每个因子只依赖于随机变量的一个子集。
比如对于因子
p
(
a
)
p(a)
p(a),没有输入的链接,也就没有箭头指向它。而对于因子
p
(
c
∣
a
,
b
)
p(c|a,b)
p(c∣a,b),存在从结点
a
,
b
a,b
a,b到结点
c
c
c的链接。
这里我们说结点
a
a
a是结点
b
b
b的父结点,结点
b
b
b是结点
a
a
a的子结点。这种关系和数据结构中的图一致。
这里要注意的是,我们隐式地选择了一种顺序来分解 p 5 p5 p5,不同的顺序会对应不同的分解方式,也得到不同的图表示。
我们看到,在图的所有结点上定义的联合概率分布由每个结点上的条件概率分布(conditional probability distribution,CPD)的乘积表示,每个条件概率分布的条件都是图中结点的父结点所对应的变量。因此,对于一个有
K
K
K个结点的图,联合概率为:
p
(
x
)
=
∏
k
=
1
K
p
(
x
k
∣
p
a
k
)
(13)
p(\pmb x) = \prod_{k=1}^K p(x_k|pa_k) \tag{13}
p(x)=k=1∏Kp(xk∣pak)(13)
其中
p
a
k
pa_k
pak表示
x
K
x_K
xK的父结点的集合;
x
=
{
x
1
,
⋯
,
x
K
}
\pmb x=\{x_1,\cdots,x_K\}
x={x1,⋯,xK}。这个公式非常重要,表示有向图模型的联合概率的分解(factorization)属性。图中每个结点还可以关联一个变量的集合。这也表示了有序马尔可夫性质(ordered Markov property)。我们来看一个例子,看马尔可夫链是如何用概率图模型表示出来的。
马尔可夫链
马尔可夫链(Markov chain)又称离散时间马尔可夫链,使用 t t t来表示时刻,用 X t X_t Xt来表示在时刻 t t t链的状态,假定所有可能状态组成的有限集合 S \cal S S称为状态空间。
马尔可夫链为状态空间中从一个状态到另一个状态的转换的随机过程。
在马尔可夫链的每一步,根据概率分布,可以从一个状态变到另一个状态,也可以保存当前状态。状态的概率叫做转移,状态改变的概率相关的概率就转移概率。
描述当前状态为
i
i
i,下一个状态为
j
j
j的转移概率
p
i
j
p_{ij}
pij定义为:
p
i
j
=
P
(
x
t
+
1
=
j
∣
x
t
=
i
)
,
i
,
j
∈
S
(14)
p_{ij} =P(x_{t+1}=j|x_t=i), \qquad i,j \in \cal S \tag{14}
pij=P(xt+1=j∣xt=i),i,j∈S(14)
马尔可夫链的核心假设是,只要时刻
t
t
t的状态为
i
i
i,不论过去发生了什么,也不论链是如何到达状态
i
i
i的,下一个时刻转移到状态
j
j
j的概率就一定是状态转移概率
p
i
j
p_{ij}
pij。即,该过程要求具备“无记忆”的性质:下一状态的概率分布只能由当前状态决定,与时间序列上它前面的事件无关。这种无记忆性称为一阶马尔可夫性质。在数学上表示为:
P
(
x
t
+
1
=
j
∣
x
t
=
i
,
x
t
−
1
=
i
n
−
1
,
⋯
,
x
0
=
i
0
)
=
P
(
x
t
+
1
=
j
∣
x
t
=
i
)
=
p
i
j
(15)
P(x_{t+1}=j|x_t=i,x_{t-1}=i_{n-1},\cdots,x_0=i_0) = P(x_{t+1}=j|x_t=i)=p_{ij} \tag{15}
P(xt+1=j∣xt=i,xt−1=in−1,⋯,x0=i0)=P(xt+1=j∣xt=i)=pij(15)
转移概率
P
i
j
P_{ij}
Pij一定是非负的,且和为1:
∑
j
p
i
j
=
1
\sum_j p_{ij} = 1
j∑pij=1
下一个状态可能和当前状态一样,即状态没有发生变化,我们也认为状态发生了一次特殊的转移(自身转移)。
一阶马尔可夫链的有向图模型表示为:
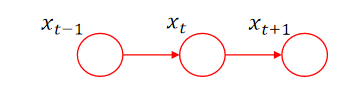
总结一下,一个马尔可夫链模型由以下特征确定:
- 状态集合 S \cal S S;
- 可能发生状态转移 ( i , j ) (i,j) (i,j)的集合,即由所有 p i j > 0 p_{ij} > 0 pij>0的 ( i , j ) (i,j) (i,j)组成;
- p i j p_{ij} pij的取值为正;
马尔可夫链可以由转移概率矩阵所刻画,它是一个简单的二元矩阵,其第
i
i
i行第
j
j
j列的元素为
p
i
j
p_{ij}
pij,假设共有
m
m
m个状态:
[
p
11
p
12
⋯
p
1
m
p
21
p
22
⋯
p
2
m
⋮
⋮
⋮
⋮
p
m
1
p
m
2
⋯
p
m
m
]
\begin{bmatrix} p_{11} & p_{12} & \cdots & p_{1m} \\ p_{21} & p_{22} & \cdots & p_{2m} \\ \vdots & \vdots & \vdots & \vdots \\ p_{m1} & p_{m2} & \cdots & p_{mm} \\ \end{bmatrix}
p11p21⋮pm1p12p22⋮pm2⋯⋯⋮⋯p1mp2m⋮pmm
也可以用转移概率图表示马尔可夫链,图中用结点表示状态,连接结点的(有向)弧线表示可能发生的转移,将
p
i
j
p_{ij}
pij的数值标记在相应的弧线旁边。
比如下面来自维基百科的一个例子,它表示一个具有两个状态转换的马尔可夫链:
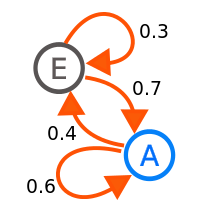
那么对于总长度为
T
T
T的
x
1
:
T
\pmb x_{1:T}
x1:T,其联合概率分布可以表示为:
p
(
x
1
:
T
)
=
p
(
x
1
)
p
(
x
1
∣
x
1
)
p
(
x
3
∣
x
2
)
⋯
p
(
x
T
∣
x
T
−
1
)
=
p
(
x
1
)
∏
t
=
2
T
p
(
x
t
∣
x
t
−
1
)
(16)
p(\pmb x_{1:T}) = p(x_1)p(x_1|x_1)p(x_3|x_2)\cdots p(x_T|x_{T-1}) = p(x_1)\prod_{t=2}^T p(x_t| x_{t-1}) \tag{16}
p(x1:T)=p(x1)p(x1∣x1)p(x3∣x2)⋯p(xT∣xT−1)=p(x1)t=2∏Tp(xt∣xt−1)(16)
对于离散型随机变量,我们可以表示对应的条件概率分布
p
(
x
t
=
k
∣
x
t
−
1
=
j
)
p(x_t=k|x_{t-1}=j)
p(xt=k∣xt−1=j)为一个二维表,称为条件概率表(conditional probability talbe,CPT)。
p
(
x
t
=
k
∣
x
t
−
1
=
j
)
=
θ
j
k
(17)
p(x_t=k|x_{t-1}=j) = \theta_{jk} \tag {17}
p(xt=k∣xt−1=j)=θjk(17)
其中
0
≤
θ
j
k
≤
1
0 \leq \theta_{jk} \leq 1
0≤θjk≤1且
∑
k
=
1
K
θ
j
k
=
1
\sum_{k=1}^K \theta_{jk}=1
∑k=1Kθjk=1。
有一阶马尔可夫假设,肯定还有二阶,那么二阶马尔可夫假设表示什么意思。类似地,二阶表示当前状态仅依赖于过去的两个状态,相应的联合概率分布可以表示为:
p
(
x
1
:
T
)
=
p
(
x
1
)
p
(
x
1
,
x
2
∣
x
3
)
p
(
x
4
∣
x
2
,
x
3
)
⋯
p
(
x
T
∣
x
T
−
2
,
x
T
−
1
)
=
p
(
x
1
,
x
2
)
∏
t
=
3
T
p
(
x
t
∣
x
t
−
2
:
t
−
1
)
(16)
p(\pmb x_{1:T}) = p(x_1)p(x_1,x_2|x_3)p(x_4|x_2,x_3)\cdots p(x_T|x_{T-2},x_{T-1}) = p(x_1,x_2)\prod_{t=3}^T p(x_t|\pmb x_{t-2:t-1}) \tag{16}
p(x1:T)=p(x1)p(x1,x2∣x3)p(x4∣x2,x3)⋯p(xT∣xT−2,xT−1)=p(x1,x2)t=3∏Tp(xt∣xt−2:t−1)(16)
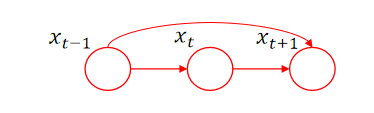
比如上面的 x t + 1 x_{t+1} xt+1,不仅依赖于 x t x_t xt,还依赖于 x t − 1 x_{t-1} xt−1。
显然,阶越高,需要描述的边就越多,模型就越复杂。
条件独立性质
我们知道了一个图可以表现出一些给定变量的符合某种条件独立的分布。
一个概率分布 p p p包含一个条件独立性(statement)集合,这个条件独立性集合称为 I ( p ) I(p) I(p)。一个图 G G G(通过缺失的边)也包含一个条件独立性集合,这个条件独立性的集合称为 I ( G ) I(G) I(G)。如果 I ( G ) ⊆ I ( p ) I(G) \subseteq I(p) I(G)⊆I(p),即图里包含的条件独立性集合是概率分布里满足的条件独立性集合的子集,那么这个图 G G G叫做这个概率分布 p p p的I-map(独立图,independency map)。换言之,如果该图没有描述分布任何非真的条件独立性,则该图是一个I-map。这使得我们可以放心地使用该图来作为概率分布 p p p条件独立性推理的代理(proxy)。注意全连接图(无缺失的边,类似空集)是所有分布的I-map。
如果一个概率分布中的所有条件独立性质都可以通过一个图反映出来,那么这个图叫做这个分布的D-map(依赖图 dependency map)。因此一个完全无连接的图是任意概率分布的D-map。
只要是 I ( p ) I(p) I(p)的子集,其对应的图就是概率分布 p p p的I-map,所以I-map可以有很多。当 I ( G ) = I ( p ) I(G)=I(p) I(G)=I(p)时,即概率分布的每个条件独立性质都可以由图反映出来,反之也成立。此时对应的图可以等价地表示这个概率分布,也叫作 p p p的P-map(完美图, perfect map)。显然,一个P-map既是I-map也是D-map。
我们现在推导 I ( G ) I(G) I(G),即来看一个DAG(有向无环图)包含了哪些条件独立性质。
D-划分
我们来看条件独立相关的图表示,我们以三个变量
a
,
b
,
c
a,b,c
a,b,c的图模型为例。
三个变量
a
,
b
,
c
a,b,c
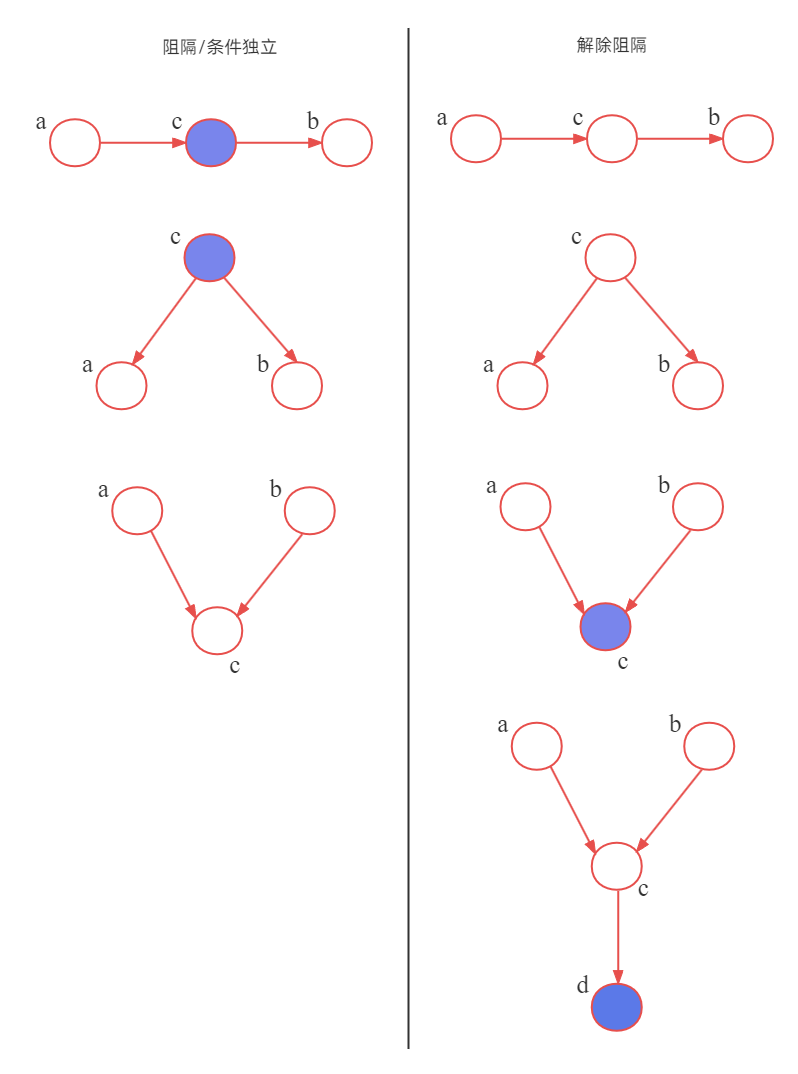
a,b,c之间的有向图连接对应三个经典的例子,我们先来看第一个。如图5所示:
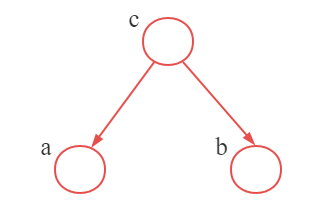
根据
(
p
6
)
(p6)
(p6),我们可以写出这个图的联合概率分布:
p
(
a
,
b
,
c
)
=
p
(
c
)
p
(
a
∣
c
)
p
(
b
∣
c
)
(17)
p(a,b,c) = p(c)p(a|c)p(b|c) \tag{17}
p(a,b,c)=p(c)p(a∣c)p(b∣c)(17)
该结构为同父结构,即结点 a , b a,b a,b存在相同的父结点 a a a。当父结点 c c c被观测到时, a , b a,b a,b条件独立。
考虑没有变量是观测变量的情形,即我们通过对
(
p
7
)
(p7)
(p7)两边进行积分或求和的方式,来考察
a
a
a和
b
b
b是否为相互独立的,即
p
(
a
,
b
)
=
∑
c
p
(
c
)
p
(
a
∣
c
)
p
(
b
∣
c
)
(18)
p(a,b) =\sum_c p(c)p(a|c)p(b|c) \tag{18}
p(a,b)=c∑p(c)p(a∣c)p(b∣c)(18)
这通常不能分解为乘积
p
(
a
)
p
(
b
)
p(a)p(b)
p(a)p(b)的形式,因此我们说:
a ⊥̸ b ∣ ∅ a \not \bot \, b \,|\, \empty a⊥b∣∅
这里 ∅ \empty ∅表示空集,符号 ⊥̸ \not \bot ⊥表示条件独立性质不总是成立。
现在假设我们以变量 c c c为条件(或者说观测到变量 c c c,即 c c c取了特定值,不再是一个随机变量),得到的图如p4所示。
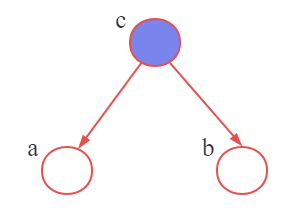
我们为上图中的结点添加阴影部分,如结点 c c c所示,表示它被观测到了。
我们可以写成给定
c
c
c的条件下,
a
a
a和
b
b
b的条件概率分布,并结合
(
17
)
(17)
(17):
p
(
a
,
b
∣
c
)
=
p
(
a
,
b
,
c
)
p
(
c
)
=
p
(
c
)
p
(
a
∣
c
)
p
(
b
∣
c
)
p
(
c
)
=
p
(
a
∣
c
)
p
(
b
∣
c
)
p(a,b|c) = \frac{p(a,b,c)}{p(c)} = \frac{p(c)p(a|c)p(b|c) }{p(c)} = p(a|c)p(b|c)
p(a,b∣c)=p(c)p(a,b,c)=p(c)p(c)p(a∣c)p(b∣c)=p(a∣c)p(b∣c)
因此,我们可以得到条件独立性质(回顾
(
9
)
(9)
(9)):
a
⊥
b
∣
c
a \,\bot \,b \,|\, c
a⊥b∣c
这里结点
c
c
c被关于关于从结点
a
a
a经过结点
c
c
c到结点
b
b
b路径的尾到尾(tail-to-tail),因为结点与两个箭头的尾部相连。
这样的一个连接结点
a
a
a和结点
b
b
b的路径的存在(从箭头头部到尾部的路径是通的)使得结点相互依赖。
然而,当我们观测到结点
c
c
c,或者说以
c
c
c为条件时,被当做条件的结点
c
c
c阻隔了从
a
a
a到
b
b
b的路径,使得
a
a
a和
b
b
b变成(条件)独立了。
路径的阻隔表示条件独立!
我们再来看第二个例子,如图7所示:
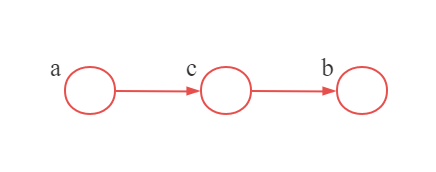
该结构称为顺序结构。当 c c c被观测到时, a , b a,b a,b条件独立。
这幅图的联合概率分布通过
(
13
)
(13)
(13)得到,形式为:
p
(
a
,
b
,
c
)
=
p
(
a
)
p
(
c
∣
a
)
p
(
b
∣
c
)
(19)
p(a,b,c) = p(a) p(c|a)p(b|c) \tag{19}
p(a,b,c)=p(a)p(c∣a)p(b∣c)(19)
与之前一样,我们对
c
c
c积分或求和来考察
a
a
a和
b
b
b是否互相独立:
p
(
a
,
b
)
=
p
(
a
)
∑
c
p
(
c
∣
a
)
p
(
b
∣
c
)
p(a,b) = p(a) \sum_c p(c|a) p(b|c)
p(a,b)=p(a)c∑p(c∣a)p(b∣c)
这一般也不能分解为
p
(
a
)
p
(
b
)
p(a)p(b)
p(a)p(b),因此
a
⊥̸
b
∣
∅
a \not \bot \, b \,|\, \empty
a⊥b∣∅
现在以结点
c
c
c为条件,再利用公式
(
19
)
(19)
(19):
p
(
a
,
b
∣
c
)
=
p
(
a
,
b
,
c
)
p
(
c
)
=
p
(
a
)
p
(
c
∣
a
)
p
(
b
∣
c
)
p
(
c
)
=
p
(
a
,
c
)
p
(
b
∣
c
)
p
(
c
)
=
p
(
a
∣
c
)
p
(
b
∣
c
)
\begin{aligned} p(a,b|c) &= \frac{p(a,b,c)}{p(c)} \\ &= \frac{p(a) p(c|a)p(b|c)}{p(c)} \\ &= \frac{p(a,c)p(b|c)}{p(c)} \\ &= p(a|c)p(b|c) \end{aligned}
p(a,b∣c)=p(c)p(a,b,c)=p(c)p(a)p(c∣a)p(b∣c)=p(c)p(a,c)p(b∣c)=p(a∣c)p(b∣c)
我们再次得到了条件独立性质:
a
⊥
b
∣
c
a \,\bot \,b \,|\, c
a⊥b∣c
结点
c
c
c被称为关于从结点
a
a
a到结点
b
b
b的路径的头到尾(head-to-tail)。这样的一个连接结点
a
a
a和结点
b
b
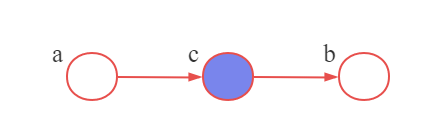
b的路径的存在使得结点相互依赖。如果我们观测结点
c
c
c,如图p6所示,这个观测阻隔了从
a
a
a到
b
b
b的路径,因此我们得到了条件独立性质。
最后,我们考虑第三个例子,也是最难理解的例子。如图p7所示:
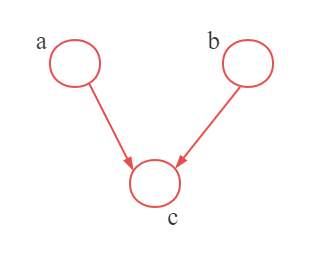
V型结构,也称冲状撞结构。当 c c c未被观测,或者说 c c c未知的情况下, a , b a,b a,b相互独立。当 c c c被观测到, a , b a,b a,b必不独立。
这里提到了给定和未知。基于条件概率 p ( A ∣ B ) p(A|B) p(A∣B),指事件 A A A在事件 B B B已经发生条件下的发生概率。事件 B B B是已经发生的,即给定的、观测到的;事件 A A A的发生是以概率形式表现的, A A A是否发生是未知的。
同样,我们可以得到联合概率分布:
p
(
a
,
b
,
c
)
=
p
(
a
)
p
(
b
)
p
(
c
∣
a
,
b
)
(20)
p(a,b,c)=p(a)p(b)p(c|a,b) \tag{20}
p(a,b,c)=p(a)p(b)p(c∣a,b)(20)
对上式两侧关于
c
c
c积分或求和,得到:
p
(
a
,
b
)
=
p
(
a
)
p
(
b
)
p(a,b)=p(a)p(b)
p(a,b)=p(a)p(b)
因为
p
(
c
∣
a
,
b
)
p(c|a,b)
p(c∣a,b)是关于
c
c
c的条件分布,也是一种概率分布,对
c
c
c求和或积分结果为
1
1
1。
这样,我们得到了和之前不一样的结果,当没有变量被观测时,
a
a
a和
b
b
b是独立的。我们可以把这个结果写成:
a
⊥
b
∣
∅
a \,\bot \,b \,|\, \empty
a⊥b∣∅
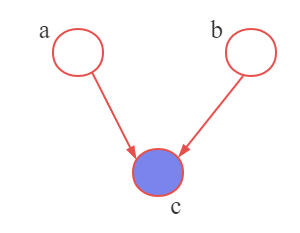
那么,假设我们还是以
c
c
c为条件,如图p8所示,有:
p
(
a
,
b
∣
c
)
=
p
(
a
,
b
,
c
)
p
(
c
)
=
p
(
a
)
p
(
b
)
p
(
c
∣
a
,
b
)
p
(
c
)
p(a,b|c) = \frac{p(a,b,c)}{p(c)} = \frac{p(a)p(b)p(c|a,b)}{p(c)}
p(a,b∣c)=p(c)p(a,b,c)=p(c)p(a)p(b)p(c∣a,b)
这通常也不能分解为
p
(
a
)
p
(
b
)
p(a)p(b)
p(a)p(b),因此,
a
⊥̸
b
∣
c
a \,\not \bot \,b \,|\, c
a⊥b∣c
图形上来看,我们说结点
c
c
c关于从
a
a
a到
b
b
b的路径是头到头(head-to-head)。当
c
c
c没有被观测到时,它阻隔了路径,使得变量
a
a
a和
b
b
b是相互独立的。当以
c
c
c为条件时,路径被解除阻隔,使得
a
a
a和
b
b
b相互依赖了。
特别地,我们考虑下图p9这种情形。是V型结构的延伸,其中新结点 d d d是结点 c c c的孩子结点,但该结构中仅 d d d被观测到,那么 a a a和 b b b也会被解除阻隔。其实,不仅是 c c c的直接孩子结点 d d d,当 c c c或 c c c的任意后继(descendant)结点被观测到,都会使得 a a a和 b b b解除阻隔。
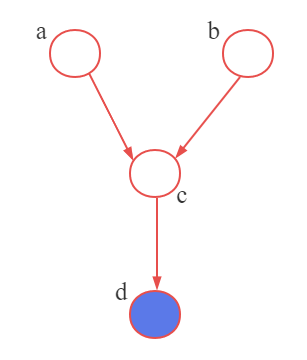
怎么证明呢?
我们还是先写出概率分布:
p
(
a
,
b
,
c
,
d
)
=
p
(
a
)
p
(
b
)
p
(
c
∣
a
,
b
)
p
(
d
∣
c
)
p(a,b,c,d) = p(a)p(b)p(c|a,b)p(d|c)
p(a,b,c,d)=p(a)p(b)p(c∣a,b)p(d∣c)
假设观测到
d
d
d,我们考虑
a
,
b
a,b
a,b是否是条件独立的。
p
(
a
,
b
∣
d
)
=
∑
c
p
(
a
,
b
,
c
∣
d
)
=
∑
c
p
(
a
,
b
,
c
,
d
)
p
(
d
)
=
∑
c
p
(
a
)
p
(
b
)
p
(
c
∣
a
,
b
)
p
(
d
∣
c
)
p
(
d
)
=
∑
c
p
(
a
)
p
(
b
)
p
(
c
∣
a
,
b
)
p
(
d
∣
c
,
a
,
b
)
p
(
d
)
=
∑
c
p
(
a
)
p
(
b
)
p
(
d
,
c
∣
a
,
b
)
p
(
d
)
=
p
(
a
)
p
(
b
)
p
(
d
∣
a
,
b
)
p
(
d
)
≠
p
(
a
)
p
(
b
)
\begin{aligned} p(a,b|d) &= \sum_c p(a,b,c|d) \\ &= \sum_c \frac{p(a,b,c,d)}{p(d)} \\ &= \sum_c \frac{ p(a)p(b)p(c|a,b)p(d|c)}{p(d)} \\ &= \sum_c \frac{ p(a)p(b)p(c|a,b)p(d|c,a,b)}{p(d)} \\ &= \sum_c \frac{ p(a)p(b)p(d,c|a,b)}{p(d)} \\ &= \frac{ p(a)p(b)p(d|a,b)}{p(d)} \\ &\neq p(a)p(b) \end{aligned}
p(a,b∣d)=c∑p(a,b,c∣d)=c∑p(d)p(a,b,c,d)=c∑p(d)p(a)p(b)p(c∣a,b)p(d∣c)=c∑p(d)p(a)p(b)p(c∣a,b)p(d∣c,a,b)=c∑p(d)p(a)p(b)p(d,c∣a,b)=p(d)p(a)p(b)p(d∣a,b)=p(a)p(b)
这里用到了 d , c , a d,c,a d,c,a和 d , c , b d,c,b d,c,b满足上面描述的顺序结构,即 p ( d ∣ a , b , c ) = p ( d ∣ c ) p(d|a,b,c)=p(d|c) p(d∣a,b,c)=p(d∣c)。
我们再考虑相反的情况,假设未观测到
d
d
d,有:
p
(
a
,
b
,
c
,
d
)
=
p
(
a
)
p
(
b
)
p
(
c
∣
a
,
b
)
p
(
d
∣
c
)
p(a,b,c,d)= p(a)p(b)p(c|a,b)p(d|c)
p(a,b,c,d)=p(a)p(b)p(c∣a,b)p(d∣c)
对上式两侧关于
d
d
d积分或求和,得到:
p
(
a
,
b
,
c
)
=
p
(
a
)
p
(
b
)
p
(
c
∣
a
,
b
)
p(a,b,c) = p(a)p(b)p(c|a,b)
p(a,b,c)=p(a)p(b)p(c∣a,b)
再关于
c
c
c积分或求和:
p
(
a
,
b
)
=
p
(
a
)
p
(
b
)
p(a,b)=p(a)p(b)
p(a,b)=p(a)p(b)
同样,当没有变量被观测到时有:
a ⊥ b ∣ ∅ a \,\bot \,b \,|\, \empty a⊥b∣∅
可以看到在未观测到 d d d的情况下, a , b a,b a,b还是互相独立的。这和结点 c c c的性质是一样的。反之,在观测到 d d d的情况下,联合概率不能分解成 p ( a ) p ( b ) p(a)p(b) p(a)p(b)。
我们可以以一个例子来简单理解,假设你家装了一个偷窃报警器,当家里遭窃或地震都有可能触发这个偷窃报警器响,而当报警器响的情况下,邻居听到后可能给你打电话。
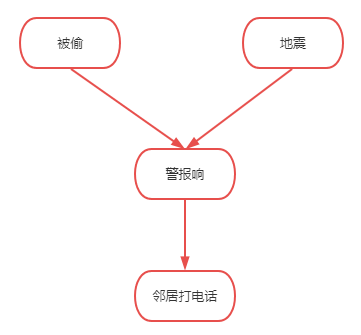
地震与否不会被你家是否遭窃影响。这里也假设小偷不管有没有地震,都不影响他进行偷窃。此时,这两个事件在报警响未被观测到的情况下,就是独立的。
假设你正在外度假,邻居给你打电话说你家报警器响了。那么从邻居打电话这个事件我们可以得到警报响这个事件发生了。
最后,我们总结成一个图:
再重申一次,若 a a a到 b b b的路径被阻隔,说明它们是(条件)独立的。
基于上面的三个例子,下面我们引入一个非常重要的概念D-划分(D-Separation),也称为有向分离,或D-分离。
图模型的一个重要且优雅的特征是,联合概率分布的条件独立性可以直接从图中读出来,不用进行任何计算。完成这件事的一般框架就是d-划分,d表示有向。
考虑一个一般的有向图,其中 A , B , C A,B,C A,B,C是任意无交集的结点集合。我们考虑从 A A A中任意结点到 B B B中任意结点的所有可能的路径,我们说这样的路径被阻隔,如果它包含一个结点满足下面两个性质中的任意一个:
- 路径上的箭头以头到尾或尾到尾的方式交汇于这个结点,且这个结点在集合 C C C中;
- 箭头以头到头的方式交汇于这个结点,且这个结点和它的所有后继都不在集合 C C C中;
如果所有的路径都被阻隔,我们说 C C C把 A A A从 B B B中d-划分开,且图中所有变量上的联合概率分布都满足 x A ⊥ G x B ∣ x C \pmb x_A \, \bot_G \, \pmb x_B \, | \, \pmb x_C xA⊥GxB∣xC。
表示
A
A
A在图
G
G
G中给定
C
C
C的情况下条件独立于
B
B
B,或给定
C
C
C的条件下
A
A
A从
B
B
B中d-分离出来:
X
A
⊥
G
X
B
∣
X
C
(21)
X_A \, \bot_G \, X_B \, | \, X_C \tag{21}
XA⊥GXB∣XC(21)
这称为(有向)全局马尔可夫性(global markov property)。
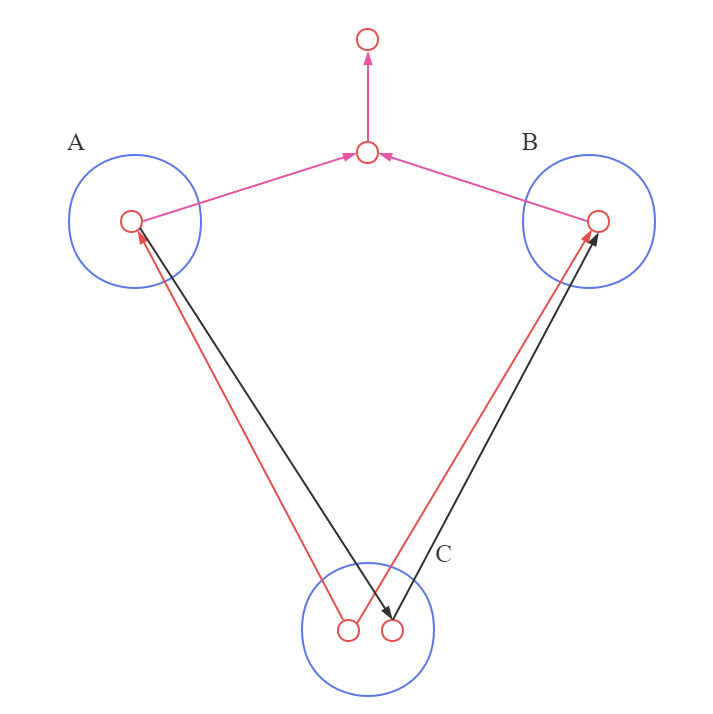
如图14所示。尾到尾是红线表示,头到尾是黑线表示,都交汇于集合 C C C中;而头到头方式交汇的结点,不在集合 C C C中。
我们再通过一个例子来理解一下,例子来自PRML。
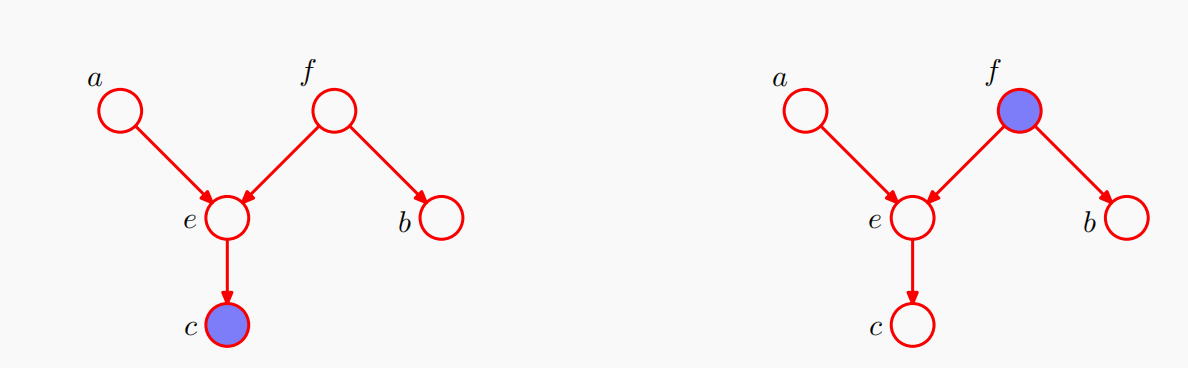
在图15左图中,从 a a a到 b b b的路径是通的,首先对于 a → e → f a \rightarrow e \rightarrow f a→e→f的路径,这是一个头到头结构,虽然 e e e未被观测到,但 e e e的后继 c c c被观测到,因此这条路径是通的,然后对于 e → f → b e \rightarrow f \rightarrow b e→f→b的路径,这是尾到尾结构,且 f f f没有被观测到,没有被 f f f阻隔;
在图15右图中,从 a a a到 b b b的路径被结点 e e e和 f f f阻隔,对于 a → e → f a \rightarrow e \rightarrow f a→e→f的路径, e e e和 e e e的后继没有被观测到(没有在条件集合中), a a a到 f f f是被阻隔的;同时对于 e → f → b e \rightarrow f \rightarrow b e→f→b来说,是一个尾到尾结构,且 f f f被观测到。因此使用这幅图进行分解的任何概率分布都满足条件独立性质 a ⊥ b ∣ f a \, \bot \, b \, | \, f a⊥b∣f。
马尔可夫毯
结点
i
i
i的马尔可夫毯是包含结点
i
i
i所有信息的结点集合,包含结点
i
i
i的:父结点、子结点、同父结点(co-parents,也就是子结点的父结点),记为
m
b
(
i
)
mb(i)
mb(i):
m
b
(
i
)
≜
c
h
(
i
)
∪
p
a
(
i
)
∪
c
o
p
a
(
i
)
(22)
mb(i) \triangleq ch(i) \cup pa(i) \cup copa(i) \tag{22}
mb(i)≜ch(i)∪pa(i)∪copa(i)(22)
其中
c
h
(
i
)
ch(i)
ch(i)表示结点
i
i
i的子结点;
p
a
(
i
)
pa(i)
pa(i)表示父结点;
c
o
p
a
(
i
)
copa(i)
copa(i)表示同父结点。
换句话说,基于马尔可夫毯(以马尔可夫毯为条件),可以将结点 i i i与图中其他结点隔离(条件独立)开。马尔可夫毯包含可推断 i i i的最少信息。
以下图16为例,有:
P
(
X
i
∣
X
−
i
)
=
P
(
X
i
∣
m
b
(
X
i
)
)
(23)
P(X_i|X_{-i}) = P(X_i|mb(X_i)) \tag{23}
P(Xi∣X−i)=P(Xi∣mb(Xi))(23)
X
−
i
X_{-i}
X−i表示图中除结点
i
i
i之外的所有结点。
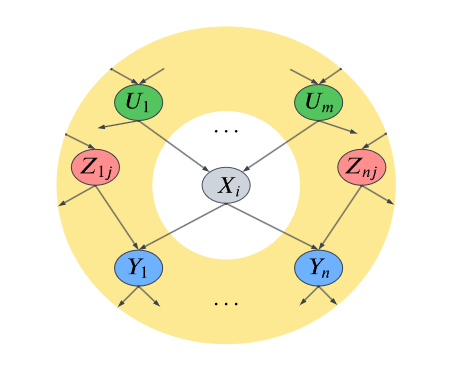
我们将概率图中所有节点分为目标结点
X
i
X_i
Xi,它的父结点
U
U
U,子结点
Y
Y
Y,同父结点
Z
Z
Z以及剩下的所有其他结点
O
O
O。我们有:
KaTeX parse error: No such environment: eqnarray* at position 8: \begin{̲e̲q̲n̲a̲r̲r̲a̲y̲*̲}̲ P(X_i|X_{-i}) …
上面等式 ( 22.1 ) (22.1) (22.1)到等式 ( 22.2 ) (22.2) (22.2)还是利用了公式 ( 13 ) (13) (13),其中 U , Z , O U,Z,O U,Z,O它们之间的关系不清楚,所以不展开。
从 ( 22.4 ) (22.4) (22.4)可以看到与 X i X_i Xi无关(没有函数依赖关系)的项在分子分母中被抵消了。只剩下结点本身的条件概率分布 P ( X i ∣ p a ( X i ) ) P(X_i|pa(X_i)) P(Xi∣pa(Xi))和 X i X_i Xi的子结点以及 X i X_i Xi的同父结点。
这样公式
(
23
)
(23)
(23)可以写成:
P
(
X
i
∣
X
−
i
)
=
P
(
X
i
∣
m
b
(
X
i
)
)
∝
P
(
X
i
∣
p
a
(
X
i
)
)
∏
Y
j
∈
c
h
(
i
)
P
(
Y
j
∣
p
a
(
Y
j
)
)
(24)
P(X_i|X_{-i}) = P(X_i|mb(X_i)) ∝ P(X_i|pa(X_i)) \prod_{Y_j \in ch(i) } P(Y_j|pa(Y_j)) \tag{24}
P(Xi∣X−i)=P(Xi∣mb(Xi))∝P(Xi∣pa(Xi))Yj∈ch(i)∏P(Yj∣pa(Yj))(24)
可能不太好理解,我们以维基百科中的图片为例,进行说明:

图17中圆圈圈起来的部分就是结点 A A A的马尔可夫毯,根据定义, A A A应该在基于马尔可夫毯的情况下独立于所有在马尔可夫毯之外的所有结点。
我们分别来验证一下。
首先来看 A A A的父节点,这里有两个父节点 B , C B,C B,C,显然这里给定 B B B能阻隔结点 A A A和 H H H(路径 H → B → A H\rightarrow B \rightarrow A H→B→A来说, B B B头到尾),同理给定 C C C能阻隔结点 A A A和 I I I。因此父节点要包含在毯中;
接着看 A A A的子结点,我们来看子结点 E E E,给定 E E E,阻隔了 A A A和 J J J以及 A A A和 K K K(以及 K K K的),因此子结点也要加到毯中;
最后看 A A A的同父结点,即 A A A的子结点的所有父结点,排除 A A A自己后有: D D D和 E E E。基于头到头结构,给定 A A A的子结点 E E E, D D D和 A A A解除阻隔, A A A与 D D D不是条件独立的,因此 A A A的同父结点也要加入到毯中。
局部马尔可夫性
基于D-划分规则,我们可以得到以下公式:
i
⊥
n
d
(
i
)
∖
p
a
(
i
)
∣
p
a
(
i
)
(25)
i \, \bot \, nd(i) \, \setminus\ \, pa(i) \,|\, pa(i) \tag{25}
i⊥nd(i)∖ pa(i)∣pa(i)(25)
其中结点
i
i
i的非后继(non-descendants)结点
n
d
(
i
)
nd(i)
nd(i)是所有结点除了它的后继,后继结点指的是结点
i
i
i的子结点,以及它的子孙结点。
n d ( i ) ∖ p a ( i ) nd(i) \, \setminus\ \, pa(i) nd(i)∖ pa(i)表示 i i i的非后继结点除去 i i i的父结点。
上式称为(有向)局部马尔可夫性质(local Markov property)。即给定 i i i的父结点, i i i与它的非后继结点(除去父结点)条件独立。
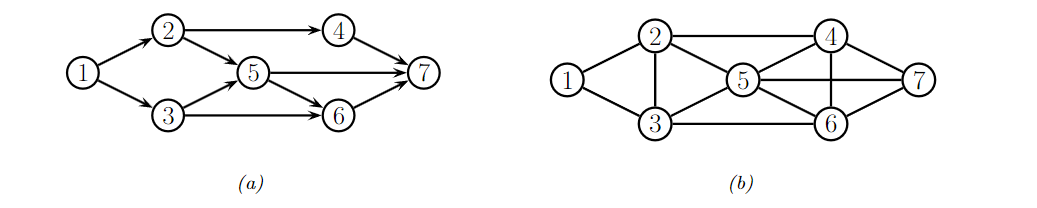
如图18(a)所示, n d ( 3 ) = { 1 , 2 , 4 } nd(3)=\{1,2,4\} nd(3)={1,2,4}。因为 5 5 5和 6 6 6是它的子结点;而 7 7 7是它的子孙结点。而 p a ( 3 ) = { 1 } pa(3)=\{1\} pa(3)={1},所以 3 ⊥ 2 , 4 ∣ 1 3 \, \bot \, 2,4 \,|\, 1 3⊥2,4∣1。
对于 3 ← 1 → 2 3\leftarrow1\rightarrow2 3←1→2来说, 1 1 1是尾到尾结构,因此观测到 1 1 1阻隔了 3 3 3和 2 2 2。
有序马尔可夫性
局部马尔可夫性的一个特例是,基于某种拓扑排序仅关注结点的前趋结点(predecessors),我们有:
i
⊥
p
r
e
d
(
i
)
∖
p
a
(
i
)
∣
p
a
(
i
)
(26)
i \, \bot \, pred(i) \, \setminus\ \, pa(i) \,|\, pa(i) \tag{26}
i⊥pred(i)∖ pa(i)∣pa(i)(26)
这是成立的,因为
p
r
e
d
(
i
)
⊆
n
d
(
i
)
。
pred(i) \subseteq nd(i)。
pred(i)⊆nd(i)。
拓扑排序(Topological Sorting)是一个有向无环图的所有顶点的线性序列。且该序列必须满足下面两个条件:
- 每个顶点出现且只出现一次。
- 若存在一条从顶点 A 到顶点 B 的路径,那么在序列中顶点 A 出现在顶点 B 的前面。
前趋结点指的是拓扑排序上出现在结点(顶点)前面的结点。
这称为有序马尔可夫性(ordered Markov property),这正是公式 ( 13 ) (13) (13)。
比如,对于图18中描述的概率图来说,如果我们使用拓扑排序为 1 , 2 , 3 , 4 , 5 , 6 , 7 1,2,3,4,5,6,7 1,2,3,4,5,6,7。那么 p r e d ( 3 ) = { 1 , 2 } pred(3)=\{1,2\} pred(3)={1,2},且 p a ( 3 ) = { 1 } pa(3)=\{1\} pa(3)={1},所以 3 ⊥ 2 ∣ 1 3 \, \bot \, 2 \,|\, 1 3⊥2∣1。
我们现在讨论了有向图的三种马尔可夫性:全局马尔可夫性 G G G(公式 ( 21 ) (21) (21))、局部马尔可夫性 L L L(公式 ( 25 ) (25) (25))以及有序马尔可夫性 O O O(公式 ( 26 ) (26) (26))。显然有 G ⇒ L ⇒ O G\Rightarrow L \Rightarrow O G⇒L⇒O,但有人证明了反之也成立。即这些性质都是相等的。
分解性质
进一步地,任何与概率图有关的分布 p p p能通过公式 ( 13 ) (13) (13)进行分解,这称为分解性质(factorization property) F F F。显然 O ⇒ F O \Rightarrow F O⇒F,同样地,反之也被证明是成立的。
我们需要了解的有向图模型知识大概就这么多,下面我们来了解无向图模型。
无向图模型
无向概率图模型(Undirected probabilistic graphical model,UPGM),也称为马尔可夫随机场(Markov random fields),和有向图模型不同,它不必为边选择一个方向。
条件独立性质
无向图模型中的条件独立性质是非常直观的,比有向图更简单。给定三个结点集合
A
,
B
,
C
A,B,C
A,B,C,我们说
X
A
⊥
G
X
B
∣
X
C
(27)
X_A \,\bot_G \,X_B \,|\, X_C \tag{27}
XA⊥GXB∣XC(27)
如果
C
C
C可以从图
G
G
G中分离开
A
A
A和
B
B
B。
如何表示分离呢?很简单,移除集合 C C C中所有的结点,以及连接的边,如果没有任何路径能使得集合 A A A中的结点到达集合 B B B中的结点,那么条件独立性质成立。这称为无向图的全局马尔可夫性。
比如,以图18(b)为例,它是图18(a)道德化的版本,何为道德化后文会介绍。我们现在只需要关注这个无向图,我们有 { X 1 , X 2 } ⊥ { X 6 , X 7 } ∣ { X 3 , X 4 , X 5 } \{X_1,X_2\} \, \bot \, \{X_6, X_7\} \, | \, \{X_3,X_4,X_5\} {X1,X2}⊥{X6,X7}∣{X3,X4,X5}。

如图19所示,此时结点1,2与结点6,7之间没有任何路径相连,它们也就变成相互独立的。
同样地,无向图也有马尔可夫毯的概念,同样非常简单,因为结点只是条件依赖于相邻结点,⽽条件独⽴于任何其他的结点。对于无向图来说,结点
t
t
t的马尔可夫毯仅由其相邻结点的集合组成,记为
m
b
(
t
)
mb(t)
mb(t)。以图中所有其他结点为条件,结点
t
t
t的条件概率分布只依赖于马尔可夫毯中的节点:
t
⊥
V
∖
c
l
(
t
)
∣
m
b
(
t
)
(28)
t \, \bot \, \mathcal{V} \setminus cl(t) \,|\, mb(t) \tag{28}
t⊥V∖cl(t)∣mb(t)(28)
这里
c
l
(
t
)
≜
m
b
(
t
)
∪
{
t
}
cl(t) \triangleq mb(t) \cup \{t\}
cl(t)≜mb(t)∪{t}是结点
t
t
t的闭包(closure),
V
\cal V
V是图中所有节点。这称为无向局部马尔可夫性(undirected local Markov property)。
比如图18(b)中,我们有 m b ( X 5 ) = { X 2 , X 3 , X 4 , X 6 , X 7 } mb(X_5) = \{X_2,X_3,X_4,X_6,X_7\} mb(X5)={X2,X3,X4,X6,X7}。
从局部马尔可夫性,我们可以容易地看到,如果两个结点在给定剩下的结点后没有边相连,那么这两个节点是条件独立的。这被称为是成对马尔可夫性(pairwise Markov property)。可以表示为:
s
⊥
t
∣
V
∖
{
s
,
t
}
⟺
G
s
t
=
0
(29)
s \, \bot \, t | \, \mathcal{V} \, \setminus \, \{s,t\} \iff G_{st} = 0 \tag{29}
s⊥t∣V∖{s,t}⟺Gst=0(29)
这里
G
s
,
t
=
0
G_{s,t}=0
Gs,t=0表示
s
s
s和
t
t
t之间没有边存在。
基于这三个马尔可夫性质,我们可以从图18(b)中的无向概率图模型推导出下面的条件独立性质:
- X 1 ⊥ X 7 ∣ rest X_1 \, \bot \, X_7 | \text{rest} X1⊥X7∣rest ,rest表示除 X 1 , X 7 X_1,X_7 X1,X7之外剩下的结点,这是成对马尔可夫性;
- X 1 ⊥ rest ∣ X 2 , X 3 X_1 \, \bot \, \text{rest} |X_2, X_3 X1⊥rest∣X2,X3, X 2 , X 3 X_2,X_3 X2,X3是 X 1 X_1 X1的马尔可夫毯中的结点,这是局部马尔可夫性;
- X 1 , X 2 ⊥ X 6 , X 7 ∣ X 3 , X 4 , X 5 X_1,X_2 \, \bot \, X_6,X_7 | X_3,X_4,X_5 X1,X2⊥X6,X7∣X3,X4,X5,给定 X 1 , X 2 X_1,X_2 X1,X2和 X 6 , X 7 X_6,X_7 X6,X7中间的三个结点,它们是条件独立的,这是全局马尔可夫性;
显然全局马尔可夫性可推出局部马尔可夫性,后者可推出成对马尔可夫性。但反之,也是成立的。因此,这些马尔可夫性也是相等的。
分解性质
因为无向图模型没有方向,因此没有一个拓扑排序,我们无法使用链式法则来表示 P ( x 1 : N ) P(x_{1:N}) P(x1:N),即来做为无向图的分解规则。因此我们需要找到无向图的一个分解规则,能对应于上面的条件独立性检测。这涉及到将联合概率分布 p ( x ) p(\pmb x) p(x)表示为在图的局部范围内的变量集合上定义的函数的乘积。我们需要得到这种情况下,局部性的一个合适定义。
假设考虑两个结点
x
i
x_i
xi和
x
j
x_j
xj,它们之间不存在连接,那么给定图中的所有其他结点,这两个结点一定是条件独立的(成对马尔可夫性)。可以表示为:
p
(
x
i
,
x
j
∣
rest
)
=
p
(
x
i
∣
rest
)
p
(
x
j
∣
rest
)
(30)
p(x_i,x_j|\text{rest}) = p(x_i |\text{rest}) p(x_j|\text{rest}) \tag{30}
p(xi,xj∣rest)=p(xi∣rest)p(xj∣rest)(30)
同样,这里用rest表示去除
x
i
,
x
j
x_i,x_j
xi,xj后图中剩余的结点集合。于是,联合概率分布的分解一定需要让
x
i
x_i
xi和
x
j
x_j
xj不出现在同一个因子中,从而让属于这个图的所有可能的概率分布都满足条件独立性质。
我们引入了一个图形的概率,团(clique)。它是图中结点的一个子集,这个子集中的任意两个结点之间都存在连接。即,团中的结点集合是全连接的。此外,一个最大团(maximal clique)是具有以下性质的团块:若 C C C是无向图 G G G的一个团,并且不能再加进任何一个 G G G的节点使其成为一个更大的团,则称 C C C为最大团。即不能再加进任何一个结点使其成为一个更大的团。
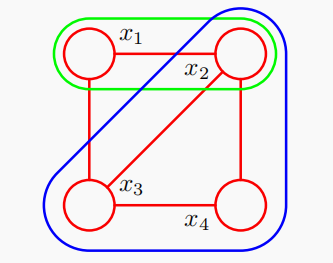
如图20,这是一个包含4个结点的无向图,图中有一个团块(绿色圈出) { x 1 , x 2 } \{x_1,x_2\} {x1,x2},但这不是一个最大团,要加入 x 3 x_3 x3之后 { x 1 , x 2 , x 3 } \{x_1,x_2,x_3\} {x1,x2,x3}才组成一个最大团;另外一个最大团是蓝色圈出的 { x 2 , x 3 , x 4 } \{x_2,x_3,x_4\} {x2,x3,x4}。从中我们可以看到最大团可能不止一个。
这样,我们可以将联合概率分布分解的因子定义为团中变量的函数,实际上,不失一般性,我们可以考虑最大团,因为其他团一定是最大团的子集。因此,如果 { x 1 , x 2 , x 3 } \{x_1,x_2,x_3\} {x1,x2,x3}是一个最大团,并我们在这个团上定义了任意一个函数,那么定义在这些变量的一个子集上的其他因子都是冗余的。
我们记团为
c
c
c,将团中的变量集合记为
x
c
\pmb x_c
xc。这样联合概率分布可以写成图中最大团的势函数(potential function)
ψ
c
(
x
c
)
\psi_c(\pmb x_c)
ψc(xc)的乘积的形式:
p
(
x
)
=
1
Z
∏
c
ψ
c
(
x
c
)
(31)
p(\pmb x) = \frac{1}{Z} \prod_c \psi_c(\pmb x_c) \tag{31}
p(x)=Z1c∏ψc(xc)(31)
这里,
Z
Z
Z也被称为划分函数(partition function),是一个归一化常数,用于对势函数进行归一化,整个式子满足概率的定义,
Z
Z
Z表示为:
Z
=
∑
x
∏
c
ψ
c
(
x
c
)
(32)
Z = \sum_{\pmb x} \prod_c \psi_c(\pmb x_c) \tag{32}
Z=x∑c∏ψc(xc)(32)
势函数也可以称为因子(factor)。这里要求势函数是严格正的,这种因子分解由Hammersley-Clifford定理来保证。
Hammersley-Clifford定理
假设一个概率分布 p p p满足无向图 G G G所示的条件独立性质,那么Hammersley-Clifford表明 p p p可以写成:
p ( x ) = 1 Z ∏ c ∈ C ψ c ( x c ) p(\pmb x) = \frac{1}{Z} \prod_{c \in \cal C}\psi_c(\pmb x_c) p(x)=Z1c∈C∏ψc(xc)
其中 C \cal C C是图 G G G中所有的最大团, Z Z Z是由以下公式给出的划分函数:
Z = ∑ x ∏ c ∈ C ψ c ( x c ) Z = \sum_{\pmb x} \prod_{c\in \cal C} \psi_c(\pmb x_c) Z=x∑c∈C∏ψc(xc)
ψ c \psi_c ψc是严格正函数。
因此我们只考虑满足 ψ c ( x c ) > 0 \psi_c(\pmb x_c) > 0 ψc(xc)>0的势函数。注意,我们不必把势函数的选择限制为具有具体的概率含义的函数,这与有向图的情形相反。有向图中,每个因子表示为对应变量以它父结点为条件的条件概率分布。
由于势函数被限制为严格大于零,因此将势函数选择为指数函数的形式更方便,即
ψ
c
(
x
c
)
=
exp
{
−
E
(
x
c
)
}
(33)
\psi_c(\pmb x_c) = \exp \{-E(\pmb x_c)\} \tag{33}
ψc(xc)=exp{−E(xc)}(33)
其中
E
(
x
c
)
E(\pmb x_c)
E(xc)被称为能量函数(energy function)。
这里联合概率分布被定义为势函数的乘积,因此总的能量可以通过将每个最大团的能量相加的方法得到。
由于势函数没有一个具体的概率意义,但对于具体的应用来说如何选择势函数成为了一个问题。可以将势函数看成一种度量,它表示了局部变量哪种配置优于其他的配置。
我们现在可以总结一下无向图和有向图的优缺点。无向概率图优于有向概率图的地方有: a) 它们是对称的,因此更适用于某些领域。 b) 从无向图可以更容易地看出条件独立性质。
但相比有向图缺点也是很明显的:a) 无向图的参数可解释性不强。b) 在使用MLE时,计算对数划分函数的导数时比较费时。
参考
- Pattern Recognition and Machine Learning
- Probabilistic Machine Learning: Advanced Topics

![[java]关于Session关于Token关于JWT](https://img-blog.csdnimg.cn/7c563572afd54f4f9fe0b2ed2fed488e.png)