0 摘要
- 学习解缠和表示数据中的变化因素是人工智能中的一个重要问题。虽然已经取得了许多关于学习这些表示的进展,但如何量化解缠仍然不清楚。
- 虽然存在一些度量标准,但对它们的隐含假设、真正衡量的内容以及限制了解甚少。
- 因此,当比较不同的表示时,很难解释结果
- 本篇论文调查了有监督的解缠度量标准,并对它们进行了深入分析。
- 提出了一个新的分类体系,将所有的度量标准分为三个类别:基于干预、基于预测器和基于信息。
- 进行了大量实验,研究了解缠表示的特性,以便在多个方面进行分层比较。
- 通过实验结果和分析,我们对解缠表示特性之间的关系提供了一些见解。
- 分享了如何衡量解缠的指南。
1 介绍
1.1 背景
- 解缠表示可以独立地捕捉解释数据的真实潜在因素。这种表示具有许多优势
- 在下游任务中使用时,可以
- 提高预测性能
- 减少样本复杂性
- 提供解释性
- 改善公平性
- 在下游任务中使用时,可以
- 最初,通过视觉检查来评估解缠度,但近年来的研究努力致力于提出更严格评估的度量标准
- 通常,随着新的表示学习方法的提出,会同时提出一种新的度量标准,以突出现有度量标准未能捕捉到的优势。
- 不幸的是,往往不清楚这些度量标准具体衡量的是什么,以及在什么条件下它们是适用的
- ——>在选择模型或超参数设置之前,必须选择一个适合的解耦程度度量标准
- 通常,随着新的表示学习方法的提出,会同时提出一种新的度量标准,以突出现有度量标准未能捕捉到的优势。
- 本文相关代码:GitHub - ubisoft/ubisoft-laforge-disentanglement-metrics
1.2 相关工作
| Challenging common assumptions in the unsupervised learning of disentangled representations ICML 2019 |
|
| A framework for the quantitative evaluation of disentangled representations, ICLR 2018 | 提出了一个评估解缠表示的框架 确定了解缠表示的三个理想属性:显性(explicitness)、紧凑(compactness)和模块化(modularity) 提出了一个由三个部分组成的新度量标准 |
2 解耦表征的特点
- 关于解缠的定义没有统一的观点,但大多数人都同意两个主要方面
- 表示必须是分布式的。
- ——>输入是解释性因素的组合,并对应于表示空间中的一个点
- 称这个点为“code,编码”。
- 每个解释性因素都在编码的不同维度中进行编码
- ——>输入是解释性因素的组合,并对应于表示空间中的一个点
- 表示还应该为下游任务编码相关信息。
- 根据应用和表示学习算法的不同,编码和因素之间的关系可能会有很大的差异
- 表示必须是分布式的。
2.1 表征中的因素独立性
- 因素独立性意味着一个因素的变化不会影响其他因素,即它们之间没有因果效应
- 在一个解缠表示中,因素在表示空间中也是相互独立的
- 换句话说,一个因素只影响表示空间的一个子集,而且只有这个因素影响这个子空间
- 不同的论文对这个属性有不同的叫法(解耦性 disentanglement,模块性 modularity)
- 论文中使用模块性
- 一些作者认为,各个受因素影响的表示空间子集应尽可能小
- 不同的论文对这个属性有不同的叫法(完整性 completeness,紧凑型 compactness)
- 但是,有的时候强制紧凑性可能会产生反效果
- 当描述复杂因素时,一组冗余的编码维度提供了更大的灵活性
- 在实践中,识别出有用且可解释的独立因素是一项具有挑战性的任务
- 因素必须在概念上独立,但也应在统计上独立
2.2 信息内容
- 一个解耦表示应该完整地描述感兴趣的解释因素
- 论文称之为明确性 explictness。
- 学习模型须将表示空间划分为与每个类别相对应的区域。
3 度量标准的特点
- 度量标准应该将最低分归因于完全随机或完全缠绕的表示,将最高分归因于完美解缠的表示
- 度量标准的分数还应该与其所测量的解缠特性的质量呈线性变化
- 解耦属性越好,得分越高
- 坏的情况是度量标准作为一个阶跃函数,这会导致分数的可解释性差,使得具有相同分数的两个模型之间的比较毫无意义
- 此外,这种行为使得度量标准非常不稳定
- 度量标准不应对超参数配置过于敏感。
- 低参数敏感性能够确保在不同配置下的稳定性。
- 对配置过度敏感的度量标准行为不可预测,可能会导致在比较模型时得出不准确的结论
- 在现实世界的应用中,数据集往往存在噪声。
- 衡量紧凑性或模块性的度量标准应该对噪声具有容忍性
- 衡量明确性的度量标准应该反映表示中的噪声量。
4 度量方法

4.0 记号
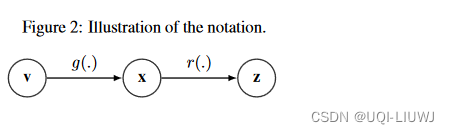
- 假设有N个observation
- 每一个observation
都假定由M个因子
完全解释,记为
- n个observation,就有n个对应的M维的v
- 每一个observation
- 一个表示学习算法希望将
映射到
(
就是前面说的‘’code“)中
- 其中
- n个observation,就被映射到n个d维的z中
- 其中
- 解耦度量是希望计算一个比较V和Z的打分
4.1 三种解耦度量方法
| 基于干预(intervention)的度量标准 | 创建在其中一个或多个因素保持不变的数据子集来比较编码 |
| 基于预测器(predictor)的度量标准 | 使用回归器或分类器从编码中预测因素 |
| 基于信息(information)的度量标准 | 利用信息论原理,如互信息(MI),来量化因素和编码之间的关系 |
4.2 基于干预的度量标准
- 固定因素(v),创建子集,比较自己中的因素(v)和编码(z)
- 采样过程需要大量不同的数据样本才能产生有意义的分数
- 主要优点是这些度量标准不对因素-编码关系做任何假设
- 缺点:超参数需要调整(数据子集的大小和数量、离散化粒度、分类器的超参数或距离函数的选择)
4.2.1 Z-diff /β-VAE
- 选择实例(x)对来创建batch
- 在一个batch中,随机选择一个因素vi
- 在vi上有相同数值的样本v1和v2
形成一个数据对
- 收集固定数量的数据对
- 用对应编码的绝对差表示这一对样本
- 子集中所有对差异的平均值创建了训练集中的一个点 (个人觉得,一个点的意思是,平均差异+哪个因素vi固定)
- 该过程重复多次以构成一个相当大的训练集
- ——>最后,在数据集上训练一个线性分类器来预测固定的因素是哪个
- 分类器的准确率就是Z-diff分数
- intuition
- 与固定因子vi相关联的编码维度应该具有相同的值
- ——>与其他编码维度相比,这个编码维度差异较小
- 与固定因子vi相关联的编码维度应该具有相同的值
4.2.2 Z-min
4.2.3 Z-max
4.2.4 IRS(Intervention Recurrence Score)
- 对因素实现进行干预之前和之后计算编码集之间的距离
- intuition
- 干扰因素的变化不应该影响与目标因素相关的编码维度
- 方法
- 首先,从实例中创建一个参考集,其中目标因素的实现被固定
- 然后,第二个集合包含具有相同目标因素实现但干扰因素实现不同的实例
- 计算与目标因素相关的编码维度的均值之间的距离
- 采样和距离测量过程重复多次,最终的score是最大距离
4.3 基于预测的方法
- 训练回归器或分类器以从编码中预测因素(f(z)→v)
- 分析预测器以评估每个编码维度在预测因素方面的有用性
4.3.1 Disentanglement, Completeness and Informativeness (DCI)
- 分别报告了模块性、紧凑性和显式性的分数。
- 他们训练回归器从编码中预测因素。通过检查回归器的内部参数来(每个因素和编码维度对的预测重要性权重Rij)估计模块性和紧凑性。
- 他们使用线性的Lasso回归器或非线性因素-编码映射的随机森林。
- 对于Lasso回归器,重要性权重Rij是模型学习到的权重的大小
- 对于随机森林,则使用编码维度的基尼重要性。
| 紧凑性 | pij 编码第j个维度对因子第i个维度重要的概率 整个表征的平均紧凑度:所有因子的平均紧凑性 |
| 模块性 | pij 编码第j个维度对因子第i个维度重要的概率 整个表征的模块性:编码每个维度的模块性Dj的加权求和 |
| 显示性 | 回归器的预测误差:1-6*MSE |
4.3.2 显性分数
- 使用简单的分类器(如逻辑回归),并使用ROC曲线下面积(AUC-ROC)来报告分类性能
- 最终得分是所有因素的所有类别的平均AUC-ROC
4.3.3 SAP
4.4 基于信息的方法
- 估计因素和编码之间的互信息(MI)来计算解缠度分数
4.4.1 MIG

- 计算每个因子和每个编码的互信息
- 最大的互信息记为
,次大的记为
- 最大的互信息记为
- H(vi)是vi的熵