导读
人类大脑是一个紧密连接的复杂系统。虽然其结构比较固定,但它可以实现很多不同的功能。其中一个重要的功能是自然睡眠过程,这个过程可以改变意识和随意肌肉活动。在神经层面上,这些改变会伴随着大脑连接的变化。为了揭示这种与睡眠相关的连接变化,本研究提出了一种重建和评估功能交互机制的方法学框架,可以分析人类整晚睡眠时的EEG记录。首先,采用时频小波变换来研究脑电波振荡的存在和强度。然后,应用动态贝叶斯推理方法对噪声干扰下的相位变化进行分析。利用该方法可以重建跨频率耦合函数,并揭示出跨频率耦合的发生和表现机制。本研究重点分析了δ-α耦合函数,并观察了这种跨频率耦合在不同睡眠阶段的变化。结果表明,从清醒到NREM3(非快速眼动)阶段,δ-α耦合函数逐渐增大,但仅在NREM2和NREM3阶段时,其替代数据检验显著。对空间分布连接的分析表明,这种显著性仅在单电极区域以及在头部前后方向上较强。本研究提出的分析方法是针对整晚睡眠记录的,但它也对其他全局神经状态具有一般意义。
前言
自然界中的许多系统都存在相互作用,可能是彼此之间的作用,或者与环境的相互作用,或者是组成它们的子系统之间的相互作用。相互作用对于像大脑这样的复杂系统尤为重要,因为它在相同的结构连接下具有许多不同的功能。复杂动力学系统的相互作用可能会引起其定性动力学的逐渐或突然变化,从而导致其分类、自组织、聚类和相互协调同步。这种动力系统的一个重要类别是振荡器,在大脑的宏观尺度上可以表现为不同的脑电波振荡。
目前已有许多有效的方法用于研究脑电波振荡及其相互作用的不同方面。通常在神经科学中,大脑连接被分为三种不同的类型。即,大脑连接是指神经系统中不同单元之间的连接模式(“结构连接或解剖连接”)、统计依赖关系(“功能连接”)和因果模型相互作用(“有效连接”)。单元之间的连接模式由结构连接(如突触或纤维路径)形成,或者表示为统计或因果关系(如互相关、相干性、信息流或耦合函数)。因此,大脑连接对于了解神经元和神经网络如何处理信息至关重要。跨频率耦合研究是一种特别可行和有用的方法,它研究不同脑电波振荡之间的连接,通常从EEG记录中提取。这项工作的重点是动态推断方法,通常也称为动态滤波或动态建模。特别是这种方法包括数据分析以重建描述系统及其相互作用的动态模型。这样,动态推断方法可以重建有效连接,从而揭示潜在的动力学机制。
所述的动态推断方法已经被开发并应用于从数据中重建耦合函数。耦合函数描述了交互是如何发生和表现的,从而能够揭示出某种功能机制。强大的方法设计和明确的耦合函数评估使其在不同的科学领域中得到了广泛的应用。可以说,最近对耦合函数的最大兴趣来自神经科学。该领域的研究工作涵盖了各种神经现象、水平和生理状态的理论和推断。当耦合函数描述具有不同频率间隔的脑电波振荡之间的相互作用时,就可以将其称为神经跨频率耦合函数。
大脑可以促进各种共存的神经状态和功能。睡眠是非常重要的状态,有助于恢复免疫、神经、骨骼和肌肉系统,维持情绪、记忆和认知功能。在生物钟的控制下,睡眠是一种精神和身体的自然周期性状态,以意识改变、感觉活动相对抑制和肌肉活动减少为特征。睡眠通常是一个相对较长的夜间过程,在这个过程中,大脑会经历几个不同的睡眠阶段。众所周知,随着睡眠的开始和睡眠阶段的不同,脑电波振荡也会发生变化。其中,最明显的两个变化出现在δ和α脑电波中。这些变化已经广泛地使用不同的频率功率和统计依赖性关系进行了研究。在研究者的早期工作中,考察了全麻和闭眼与睁眼静息态中的神经耦合函数。然而,到目前为止,尚未有研究重建和评估与睡眠及其不同睡眠阶段有关的耦合函数。在这项工作中,本文提出了一种从睡眠EEG数据中研究δ-α神经跨频率耦合函数的方法框架,并评估了与不同睡眠阶段相关的耦合函数变化。
实验程序
睡眠记录
本研究使用的EEG数据集来自DREAMS数据库。由20名(16女/4男)健康被试的整夜PSG记录组成。使用32导EEG系统(BrainnetTM System of MEDATEC,Brussels,Belgium)采集数据。每次记录至少使用三个EEG通道(CZ-A1或C3-A1、FP1-A1和O1-A1)、两个EOG通道(P8-A1、P18-A1)和一个下颌肌EMG通道。采样率设置为200Hz。根据Rechtschaffen和Kales(R&K)以及美国睡眠医学学会(AASM)方案对每晚的睡眠阶段进行评分。本研究使用AASM标准进行睡眠阶段分析。对于小波分析以及后续的耦合分析,按照AASM评分对各个睡眠阶段的结果进行分组,即将清醒、NREM1(非快速眼动睡眠阶段)、NREM2、NREM3和REM(快速眼动)睡眠阶段的小波和耦合结果分开。
时频小波分析
本文从振荡的存在和强度以及因果相互作用机制两个方面,对睡眠过程中神经振荡的相互作用进行了全面的分析。为了计算有效的神经跨频率耦合,本研究首先观察了不同睡眠周期中的神经振荡,即脑电波。通过对EEG信号进行连续小波变换(WT)分析来实现。它是一种时频表征,包含所分析信号中振荡元素的相位和振幅动态。
EEG信号x(t)的连续小波变换如下:
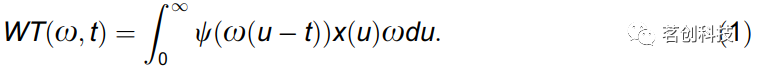
其中,ω表示角频率,t为时间,
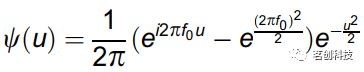
为复Morlet小波,中心频率f0=1,∫ψ(t)dt=0,i为虚数单位。
将公式(1)归一化后,|Ws(t,F)|2表示在每个时间t上的功率谱的瞬时估计,被称为小波功率。它类似于傅里叶变换功率谱,但通过使用自适应窗口,它实现了对数频率分辨率和高频以及时域局部化,允许在观测频率下适当地表征频谱结构。从脑电信号中提取的各频段分别为δ=0.8-4Hz;θ=4-7.5Hz;α=7.5-14Hz;β=14-22Hz;γ=22-100Hz。本研究利用小波变换探索了不同睡眠周期下脑电波振荡的存在性,以及它们各自的强度。
神经耦合函数
大脑是一个高度连接的复杂系统,其相互作用可以在不同层面上进行研究,其中许多相互作用对特定的神经状态和疾病具有重要的意义。耦合函数对于研究神经相互作用特别有吸引力,因为它们可以表征这些连接背后的特定神经机制。本文从系统设置的角度研究交互动力学系统,重点关注耦合振荡器。然后,耦合函数描述了指定交互作用如何发生和显示的物理规则。由于耦合函数与函数依赖直接相关,因此耦合函数不仅关注是否存在交互,而且更关注它们如何出现和发展。例如,当研究耦合振荡器的相位动力学时,相位耦合函数的大小直接影响振荡频率,并描述了振荡是如何受到另一个振荡器的影响而加速或减速的。
相互作用振荡的相位动力学模型。本研究将整个神经相互作用系统建模为成对耦合相位振荡器的网络。该振荡器网络定义为:
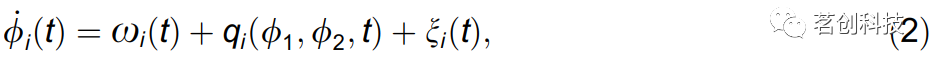
其中i=1,2是振荡器指数,ξi是高斯白噪声,φi是每个振荡器的瞬时频率,该频率由其固有频率ωi和两个振荡器的相位φ1,2的耦合函数qi决定。函数qi代表了网络内部成对相互作用的潜在耦合动力学。由于系统的振荡性质,(2)的确定性部分可以用二阶傅里叶展开为基函数Φk的和,即全(φ1,φ2)参数空间上的一系列sin和cos函数,由参数缩放:
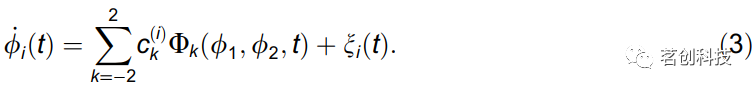
因此,主要目的是推导耦合相位振荡器的模型,即推导模型基函数Φk的参数和噪声参数。
动态贝叶斯推理
为了进行模型推理,本研究应用了动态贝叶斯推理。该方法重建参数矩阵M={,D},由耦合参数和噪声强度D组成,从而完整地描述了振荡器的耦合。通过利用贝叶斯定理的本质,在给定数据X和给定参数的先验概率密度pprior(M)的情况下,得到未知参数M的后验概率密度pX(M|X):
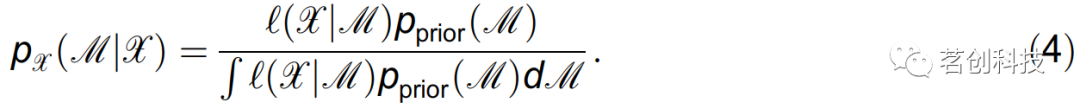
这里,通过对噪声项随时间的随机积分得到似然函数l(M|X),因此得到负对数似然函数S=-lnl(M|X)定义为:
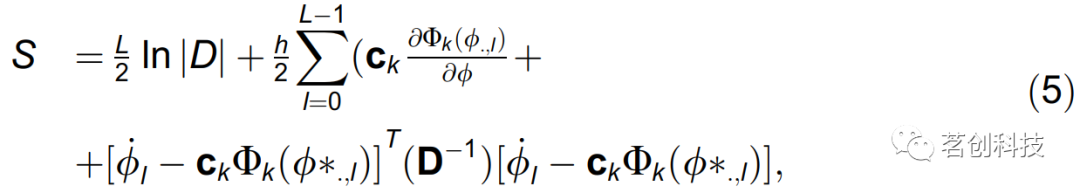
其中h是采样时间,L是时间序列的长度,对k的求和是隐式的。
假设参数M的先验概率是多元正态分布。然后,考虑到对数似然(5)为二次型,后验概率也将是多元正态分布。然后利用参数向量c的分布、及其均值和协方差矩阵递归地得到S的平稳点:
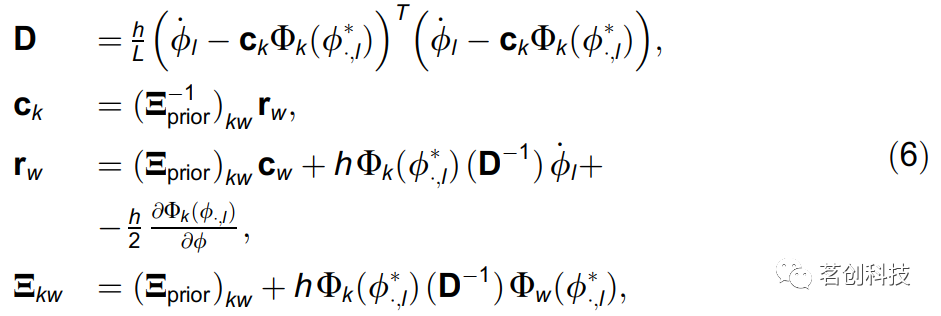
最后,振荡器1到振荡器2的耦合强度是由相位动力学推导出的欧氏范数:

这里描述的推理所需的神经输入数据以瞬时相位信号的形式提供。在实际应用中,采用标准巴特沃斯滤波器滤除EEG信号中的脑电波振荡,再进行filtfilt处理以确保无滞后干扰。然后对滤波后的振荡信号进行希尔伯特变换得到原相位,然后进行原相位到相位单变量变换,以获得作为贝叶斯推理输入的相位信号。
统计分析和替代时间序列检验
即使是不相关或非耦合的振荡,信号之间的耦合通常是正的,无论多么小。这就是为什么必须定义一个显著性阈值,超过该阈值的耦合将被认为是显著的,并表明真正的连接和相互依赖关系。该阈值是通过构建原始信号的随机替代信号,并计算这些替代信号的耦合函数来定义的。所得结果作为基准参考,以确认原始信号耦合的统计显著性。本研究使用了一个替代阈值,即均值加上从替代值计算出的耦合的两个标准差,并且为了生成替代时间序列,本研究使用了循环相位置换(CPP)替代值。为了计算耦合分布之间的统计差异,本研究使用标准的Wilcoxon统计检验,显著性水平为p<0.05。不同的耦合分布不形成统计族,不需要多重比较检验。为了直观地展示统计差异,本研究使用标准箱线图(standard boxplot),包含相应的描述性统计量(中位数、四分位数、最大值和最小值)。
结果
脑电波振荡的存在和强度
为了观察不同振荡的强度,本研究使用小波变换(WT)分析。图1A显示了被试在夜间睡眠期间的脑电信号,O1电极作为小波分析的输入信号。时频小波变换(图1B)显示了整个夜间睡眠的详细频率和时间变化。然后,图1C显示了时间平均频率小波变换,其中可以观察到特定的δ和α振荡。图1A、B和C在时间(A和B)和频率(B和C)上对齐,以便进行比较。这些结果表明,存在明显的δ和α振荡(图1C),并且这种频率功率在睡眠期间随着时间的推移而变化(图1A)。
δ脑波振荡的小波功率在不同睡眠阶段是不同的(图1D)。即清醒状态下的功率在REM睡眠阶段显著降低,然后在NREM1、NREM2和NREM3阶段逐渐增加。这里应该注意的是,NREM3中的δ功率是最高的,甚至比清醒阶段还要高。α脑波振荡的小波功率在清醒阶段最高,在之后的睡眠阶段显著降低(图1E)。这里的REM略低于其他三个NREM阶段,而这三个NREM阶段的小波功率相对相同。
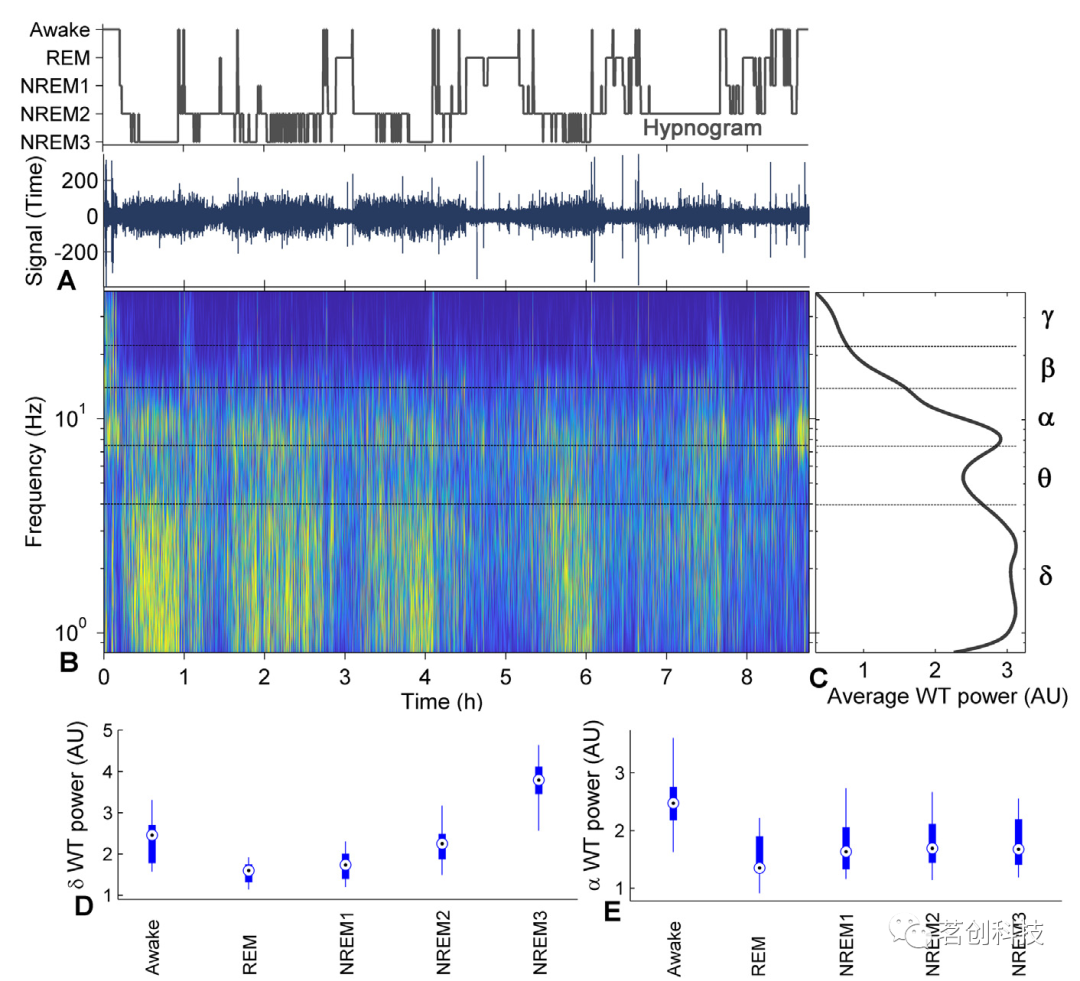
图1.睡眠中的脑电波振荡-小波变换分析。
δ-α神经耦合函数
在对EEG数据的相位进行动态贝叶斯推理后,本研究重建了δ-α耦合函数,如图2所示。对不同睡眠阶段的耦合函数进行平均。注意,为了比较不同阶段之间的耦合,耦合函数从清醒阶段到NREM3按从左到右的顺序对齐。可以看到,清醒阶段的耦合函数非常低,具有变化和不确定的函数形式(图2A)。REM睡眠和NREM1耦合函数的结果是类似的(图2B和C),并且同样具有变化和不确定的函数形式。然后,对于NREM2和NREM3阶段,δ-α神经耦合函数显著增加,并具有特征波形(图2D和E)。这种变化是渐进的,NREM3阶段的耦合函数幅值高于NREM2阶段,而NREM2阶段的耦合函数幅值又高于其他三个阶段的耦合函数。
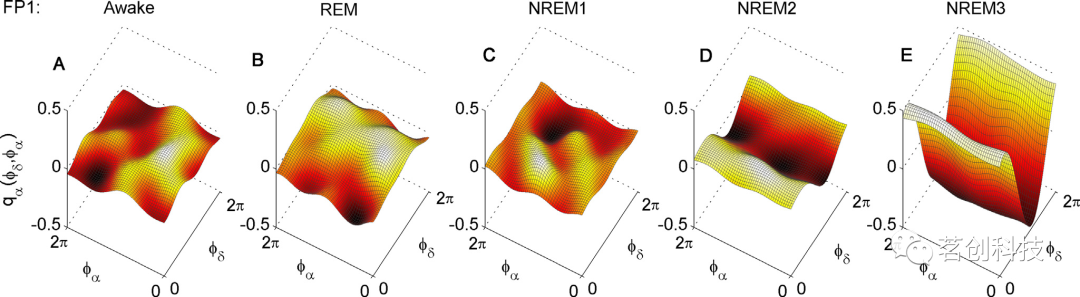
图2.睡眠中的δ-α神经耦合函数。
δ-α耦合强度
为了定量研究相互作用,本研究计算了δ-α耦合强度,作为上述δ-α耦合函数的范数。图3中的箱线图显示了被试在不同睡眠阶段的耦合强度。只有NREM2和NREM3睡眠阶段的耦合强度相对于替代阈值是显著的(如图3虚线所示)(这一定量结果与图2中NREM2和NREM3的耦合函数观测结果一致)。睡眠阶段的箱线图之间也存在差异。清醒阶段的耦合度最低,并且与其他四个睡眠阶段显著不同。REM和NREM1阶段相似,均显著大于清醒阶段,而小于NREM2和NREM3阶段。NREM2和NREM3阶段的耦合相似,并且显著大于其他三个睡眠阶段。从五个阶段的比较来看,总体趋势是从清醒到NREM3阶段的耦合强度逐渐增加。
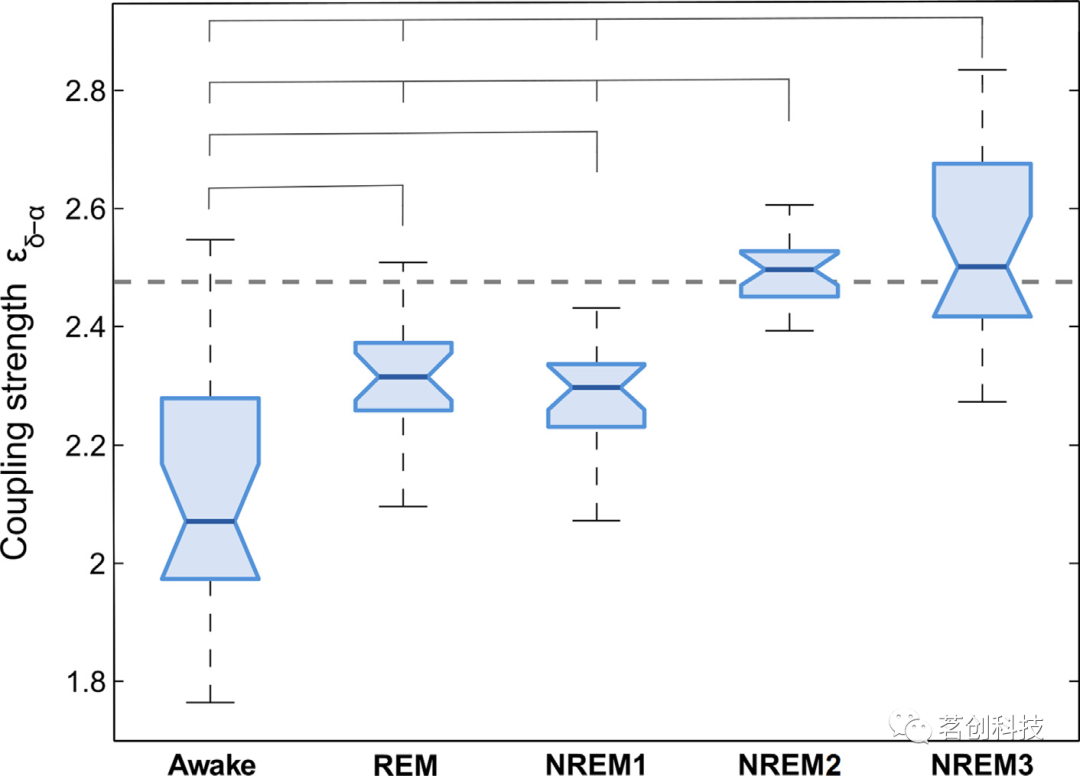
图3.平均δ-α耦合强度。
空间距离耦合函数
接下来,本研究分析了一个通道的δ波和来自另一个通道的α波在空间上的δ-α耦合函数。图4展示了耦合强度最高的NREM3睡眠阶段的这种空间δ-α耦合函数的四个例子。图4A、B分别为前后δCz-αO1和δFp1-αO1的耦合函数,其耦合函数形式与图2相同,同时具有较高的振幅,即耦合强度。图4C、D分别为后前δO1-αCz和δO1-αFp1的耦合函数,其振幅和耦合强度要小得多。然而,C和D中的耦合函数形式与A和B中的形式是相似的。这些结果表明,无论是在耦合强度还是函数形式上,NREM3睡眠阶段的耦合函数都是最强和最突出的。
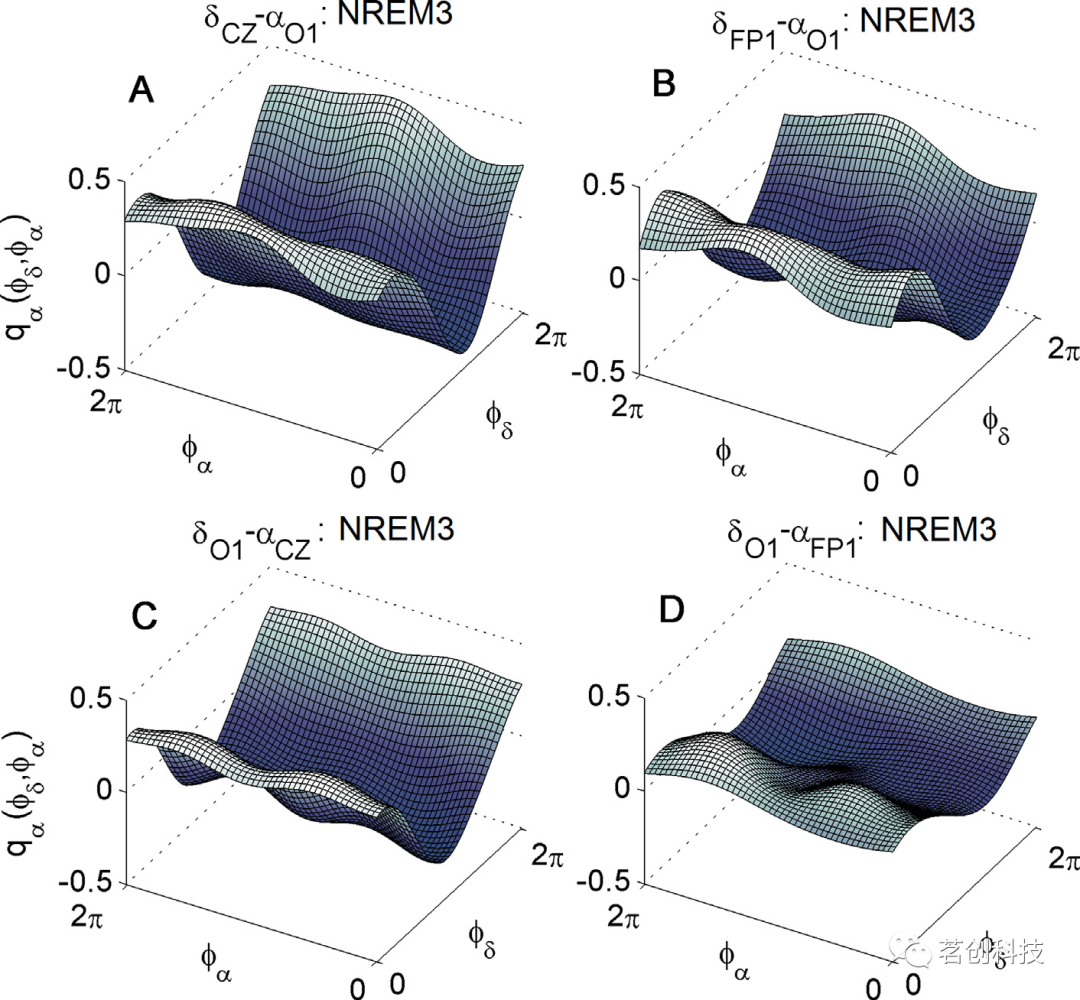
图4.睡眠中的空间δ-α神经耦合函数。
与睡眠纺锤波的类比和关系
本研究的主要重点是delta(δ=0.8-4Hz)和alpha(α=7.5-14Hz)波振荡以及它们如何通过其相位动态相互作用。另一方面,许多关于EEG动态和睡眠的研究工作已经考察了慢波(<4Hz)和纺锤波(11-16Hz)的相互作用。由于本研究分析的α频段和睡眠纺锤波的频段(σ)在频谱上有很大的重叠,因此自然地引发了一个问题,即观察到的相互作用是否反映了从δ到一个或另一个频段的相互作用,以及它们如何与不同的睡眠阶段相关联。为了理解这一点,本研究按照之前的方法对以下相互作用分别进行了分析:(i)δ-α(α´=8-12Hz)和(ii)δ-纺锤波sigma(σ=12-16Hz)。(请注意,由于与最初的α频段区间有所不同,因而这里使用α´来表示)。
此外,有许多睡眠研究将纺锤波分为两部分:慢速纺锤波(σ1=9-12Hz)和快速纺锤波(σ2=12-15Hz),然后研究它们如何与慢波相互作用。从这个意义上说,本研究对α和σ的分段与将纺锤波分为慢速和快速纺锤波的方法类似。
关于δ-α´和δ-σ耦合的分析结果如图5所示。δ-α´相互作用的耦合强度定量和统计分析如图5A所示,从清醒阶段到NREM3的耦合逐渐增强,部分耦合与替代值相比显著(例如NREM2和NREM3),并且在不同睡眠阶段之间存在显著的统计学差异。另一方面,δ-σ耦合强度图如图5B所示,耦合强度相对较低,并且与替代值相比差异不显著。δ-α´耦合函数(图5C)虽然有一些显著的耦合,但其函数形式变化更大,与之前在图2中观察到的形式相似,特别是在NREM2和NREM3睡眠阶段。综合α´和σ相位动态分析可以发现,观察到的相互作用主要是由于δ-α´耦合,而δ-σ耦合较低且不显著。
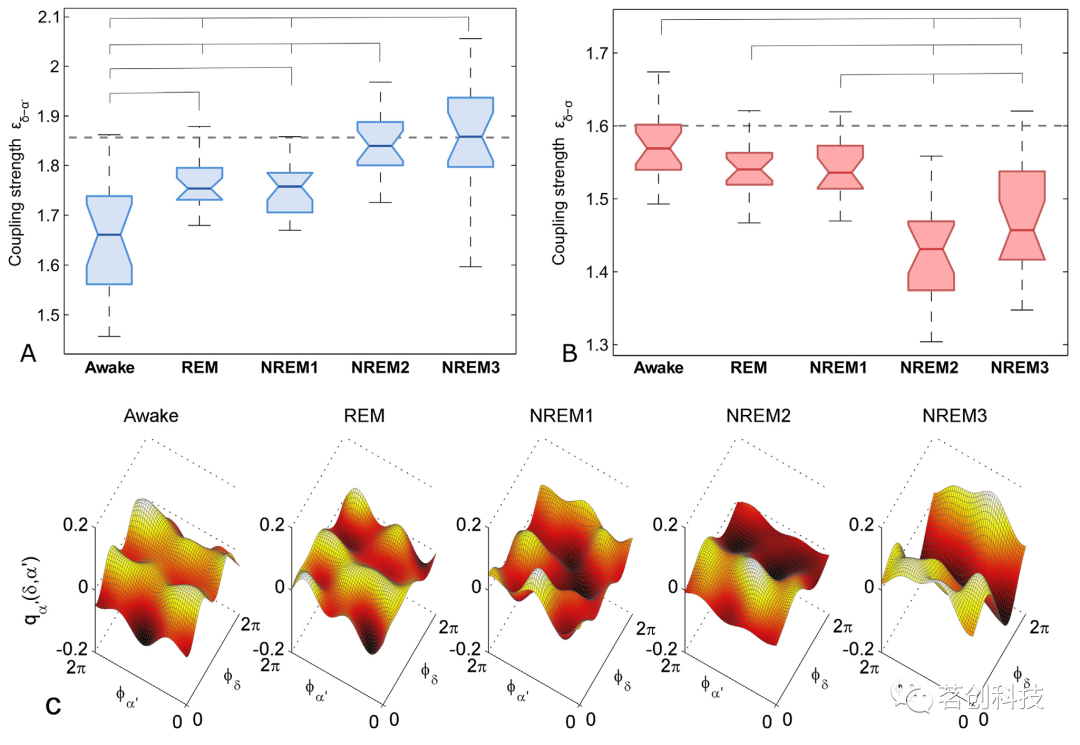
图5.睡眠中的δ-α´和δ-σ神经耦合。
结论
综上所述,本研究分析了睡眠对神经振荡动力学和相互作用的影响,提出了一种分析振荡及其相互作用机制的方法学框架。从某种意义上说,该框架是相当全面的,它包括描述振荡存在和强度的小波变换,然后是详细的相位动力学和潜在耦合函数的动态贝叶斯推理,以明确地揭示相互作用机制。这种方法直接探索了神经振荡动力学以及它们如何因果地影响以加速或减速其振荡的机制。该分析能够遵循时间演变的动态,以便追踪不同睡眠阶段的转变。因此,我们能够对特定睡眠阶段的时间间隔进行分类和平均。通过这种方式,本研究确定了睡眠阶段δ-α耦合函数的一种特定形式。最后值得注意的是,本研究提出的整夜睡眠记录方法框架具有重要的意义,并且可以轻松地用于其他形式的睡眠记录,或者更广泛的神经状态。
原文:D. Manasova, T. Stankovski, Neural Cross-Frequency Coupling Functions in Sleep, Neuroscience (2023), doi: https://doi.org/10.1016/j.neuroscience.2023.05.016