300 最长递增子序列

求数组最长严格递增子序列的长度。

$D[i]$代表以$nums[i]$结尾的最长递增子序列的长度。
$$D[i]=\underset{j<i,nums[i]>nums[j]}{\max }(D[j]+1)$$
Q1：$O(n^2)$版本如何提速到$O(n\log n)$？

Q2：能否输出路径？这个不难，增加一个$record$​数组就好。

---

写了第二遍了，但完全找不到贪心+二分查找的记忆……但看了一遍又不得不感叹巧妙。

贪心思想：保持长度为$i$的递增子序列，尾部元素值最小。比如[1,2,3,5]和[1,2,3,4]，优先选择$[1,2,3,4]$。

维护一个列表$tail$，$tail[i]$表示长度为$i+1$的递增子序列，能够获得的最小尾部元素值。

• 当$nums[i]$大于$tail$数组的最后一个有效元素时，将其放在$tail$数组的最后；
• 否则插入$nums[i]$，若$tails[j-1]<nums[i]\le tails[j]$，则插入$nums[i]$到位置$j$。

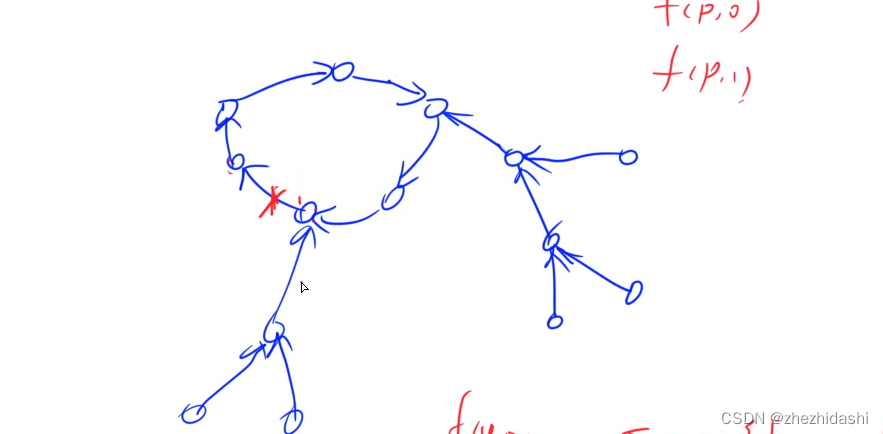
注意：$tail$数组中的元素并不一定是路径，反例为下图中蓝色部分。

674 最长连续递增子序列

$$D[i]=nums[i]>nums[i-1]?D[i-1]+1:0$$

class Solution {
    public int findLengthOfLCIS(int[] nums) {
        int maxLength = 1;
        int length = 1;
        for (int i = 1; i < nums.length; i++) {
            length = nums[i] > nums[i - 1] ? length + 1 : 1;
            maxLength = Math.max(length, maxLength);
        }
        return maxLength;
    }
}

718 最长重复子数组

给定两个数组，返回两个数组中公共的、长度最长的子数组。

令$D[i,j]$表示以$nums1[i]、nums2[j]$结尾的公共子数组最大长度。

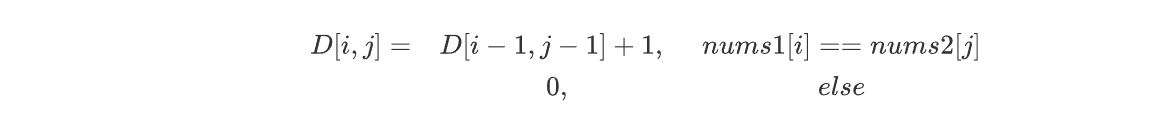
TODO：滑动窗口解法。

class Solution {
    public int findLength(int[] nums1, int[] nums2) {
        int m = nums1.length;
        int n = nums2.length;
        int[][] D = new int[m][n];
        int max = Integer.MIN_VALUE;

        for (int i = 0; i < m; i++) {
            D[i][0] = nums1[i] == nums2[0] ? 1 : 0;
            max = Math.max(D[i][0], max);
        }

        for (int j = 0; j < n; j++) {
            D[0][j] = nums1[0] == nums2[j] ? 1 : 0;
            max = Math.max(D[0][j], max);
        }

        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                D[i][j] = nums1[i] == nums2[j] ? D[i - 1][j - 1] + 1 : 0;
                max = Math.max(D[i][j], max);
            }
        }

        return max;
    }
}

1143 最长公共子序列

令$D[i,j]$表示$nums1[0:i]、nums[0:j]$的公共子序列最大长度。

class Solution {
    public int longestCommonSubsequence(String text1, String text2) {
        char[] str1 = text1.toCharArray();
        char[] str2 = text2.toCharArray();
        
        int m = str1.length;
        int n = str2.length;
        int[][] D = new int[m][n];

        D[0][0] = str1[0] == str2[0] ? 1 : 0;
        for (int i = 1; i < m; i++) {
            D[i][0] = D[i - 1][0] == 1 || str1[i] == str2[0] ? 1 : 0;
        }

        for (int j = 1; j < n; j++) {
            D[0][j] = D[0][j - 1] == 1 || str1[0] == str2[j] ? 1 : 0;
        }

        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                D[i][j] = str1[i] == str2[j] ? D[i - 1][j - 1] + 1 : Math.max(D[i - 1][j], D[i][j - 1]);
            }
        }

        return D[m - 1][n -1];
    }
}

1035 不相交的线

感觉和上一题是一样滴耶。

令$D[i,j]$表示$nums1[0:i]、nums[0:j]$最多不相交的线的数量。

class Solution {
    public int maxUncrossedLines(int[] nums1, int[] nums2) {
        int m = nums1.length;
        int n = nums2.length;

        int[][] D = new int[m][n];
        D[0][0] = nums1[0] == nums2[0] ? 1 : 0;
        for (int i = 1; i < m; i++) {
            D[i][0] = D[i - 1][0] == 1 || nums1[i] == nums2[0] ? 1 : 0;
        }
        for (int j = 1; j < n; j++) {
            D[0][j] = D[0][j - 1] == 1 || nums1[0] == nums2[j] ? 1 : 0;
        }

        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                D[i][j] = nums1[i] == nums2[j] ? D[i-1][j-1] + 1 : Math.max(D[i][j - 1], D[i - 1][j]);
            }
        }

        return D[m - 1][n - 1];
    }
}