一、Dijkstra的用途

Dijkstra算法是用来解决边权不是一，并且时，单源最短路问题的。好的，大概率这句话没有看懂。没关系的，接下来将通俗地说明一下。

边权是指边的长度，也就两个点之间的距离。单源指的是从同一个起点出发，前往不同的点。

例如下图所示：

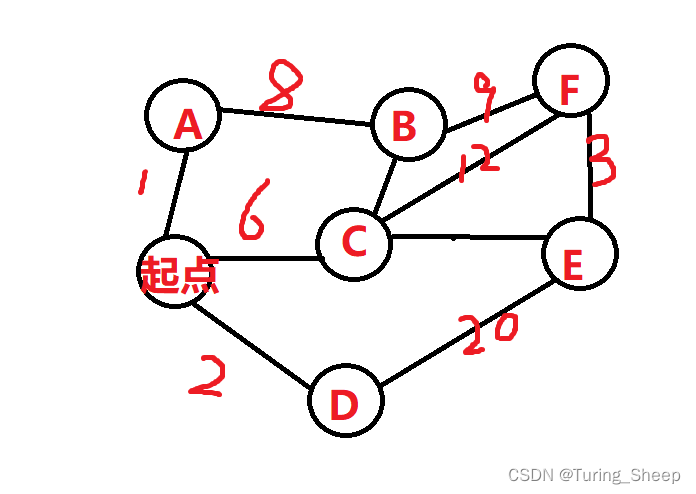
那么从起点到某个点的最短路径问题，就是我们的dijkstra算法需要解决的问题。

二、Dijkstra的思想及证明

（1）相关结论及证明：

结论1：必须借助中间点时

某个点到终点的最短路程＝该点到中间点的最短距离＋中间点到终点的最短距离

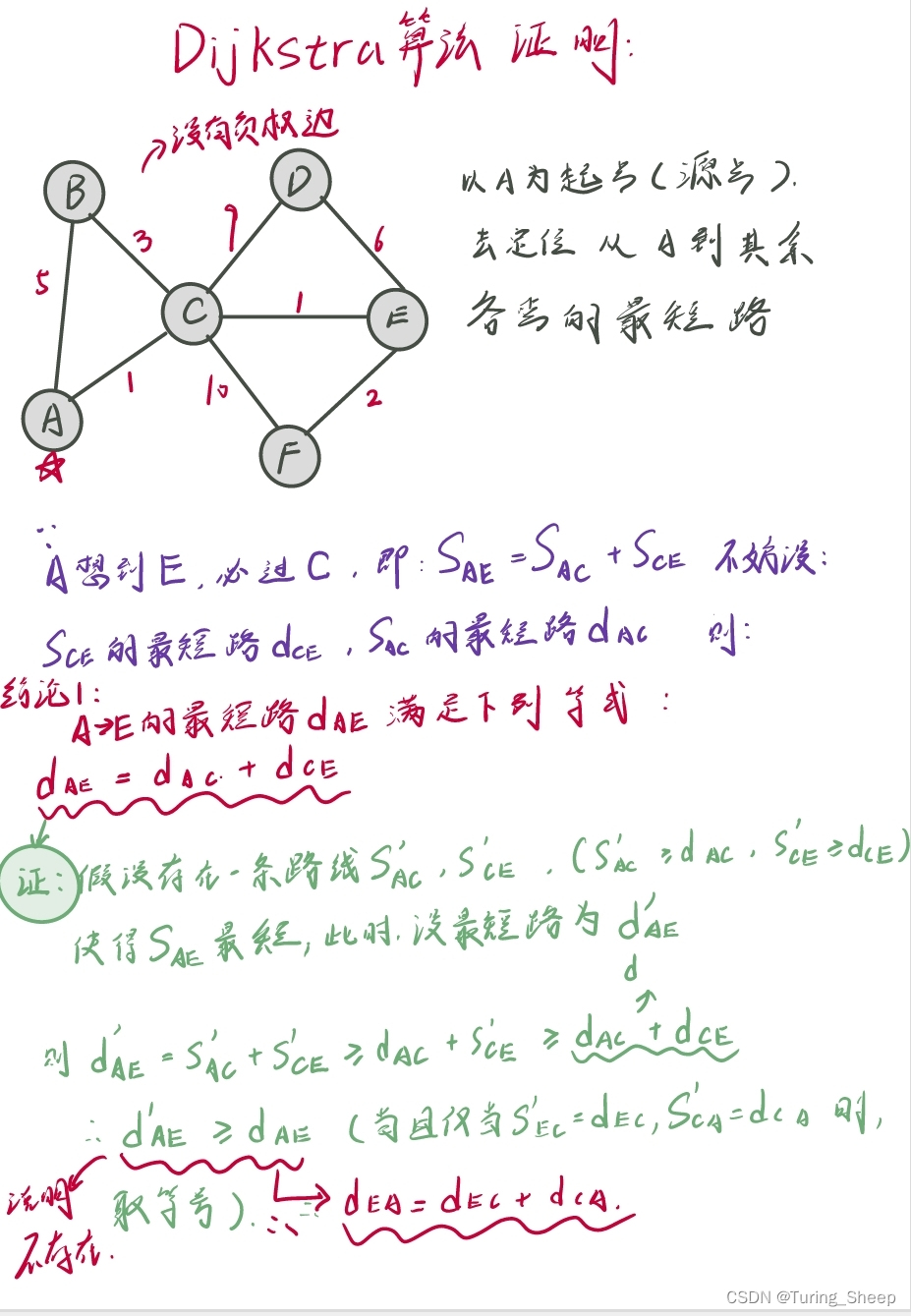
结论2：存在不借助中间点的情况

若该点C是A点邻接点中距离A点最近的点，则从该点A直接到C的路线就是各种其他路线中最近的。

以上就是dijkstra算法的两个核心结论，接着作者将使用这两个结论还原dijkstra算法！

（2）算法整体思路：

a、理解方式1：结论1+结论2+枚举

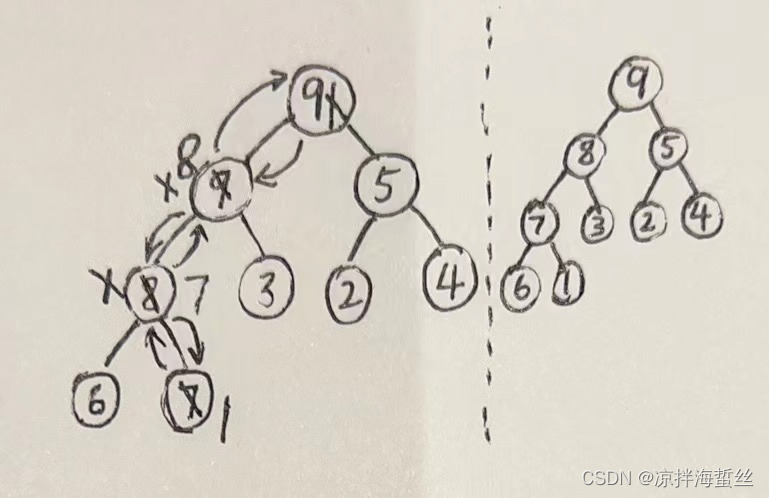
我们看下面的图：

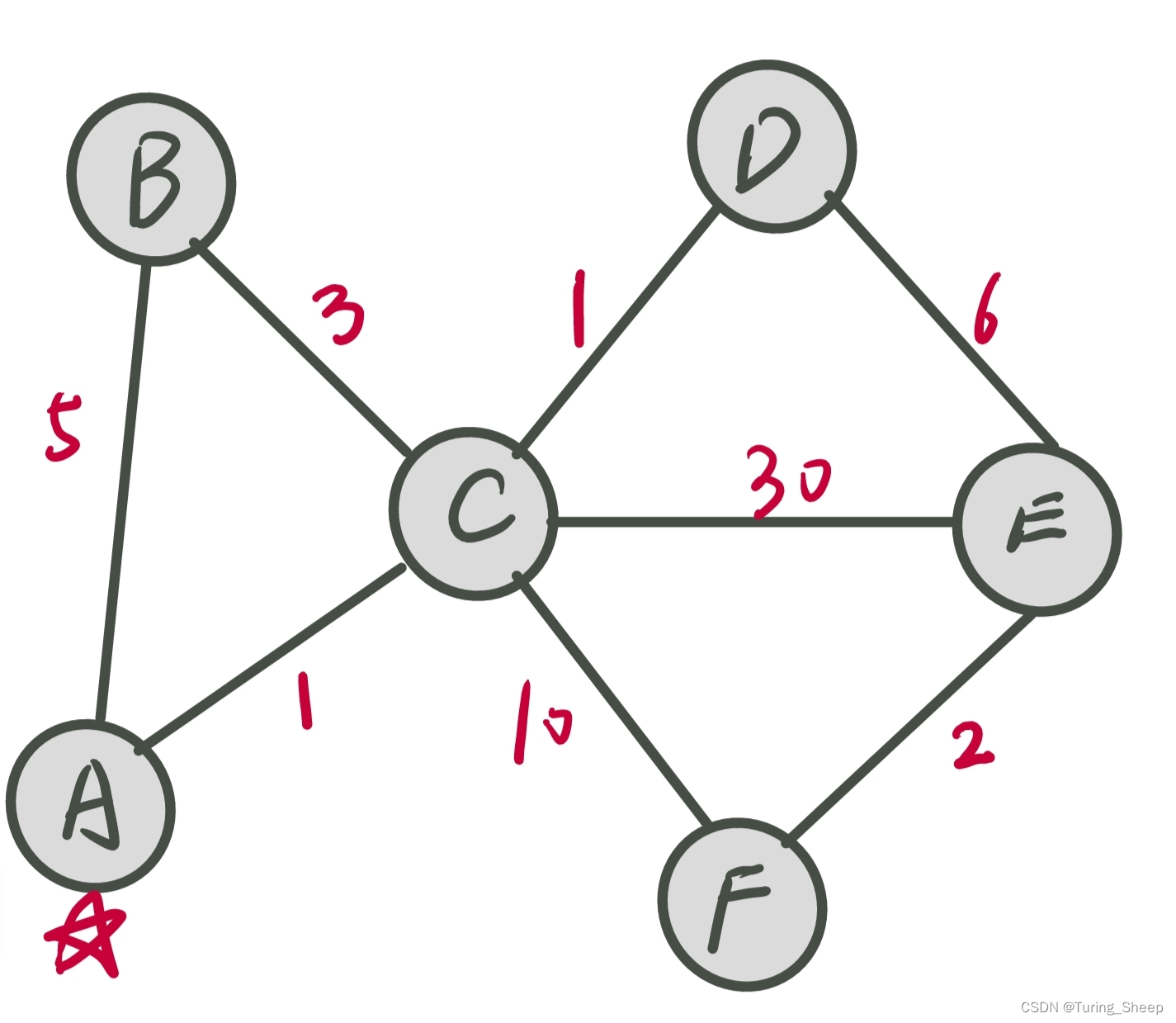
下表存储的是没有计算出最短路的点到A的距离：

我们从A点出发，发现A点经过的邻接点是C和B，那么我们记录一下C和B到A的距离。

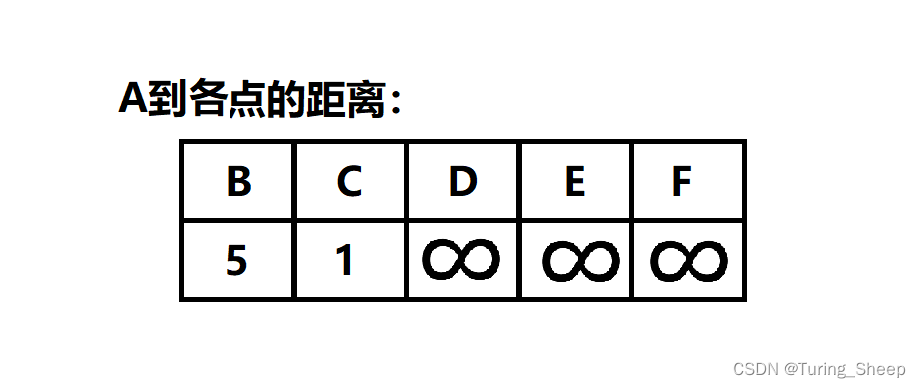
下表存储的是已经计算出最短路的点到A的距离：

我们发现，通过图中的表来看距离A的最短邻接点是C，所以根据我们的结论2，A到C的最短距离就是1。因此，我们就可以把C拿出这个表了。

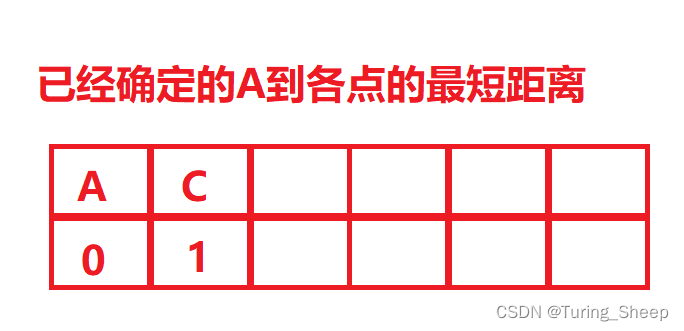
那么我们找到了AC的最短路后，我们可以尝试一下能否用一用结论1，我们看看能否找到C的最近邻接点。

那么怎么办呢？我们找一下C的邻接点：B、D、E，那么此时AB的距离就是AC+BC，以此类推。
（起点到终点和终点到起点的最短路是一致的，这里反过来想更容易理解。以下将倒过来讲解）

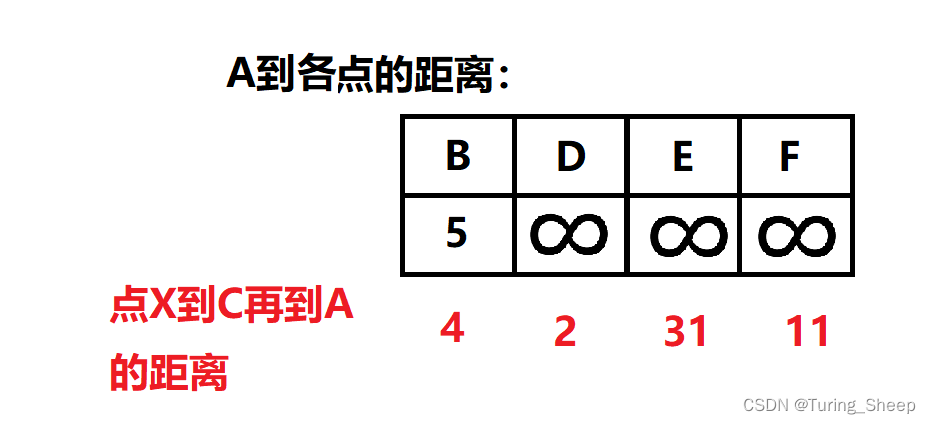
因为上述红色数字是利用：XC+AC，所以上述表中的大小关系，就是某个X到C的距离的大小关系。因此，CD是最短的。根据结论1：AX的最短路＝XC的最短路＋AC的最短路，AD最短的距离就是2，因此我们拿出D点，放入红表中。（这里判断XC的最短路，同样用到了结论2）

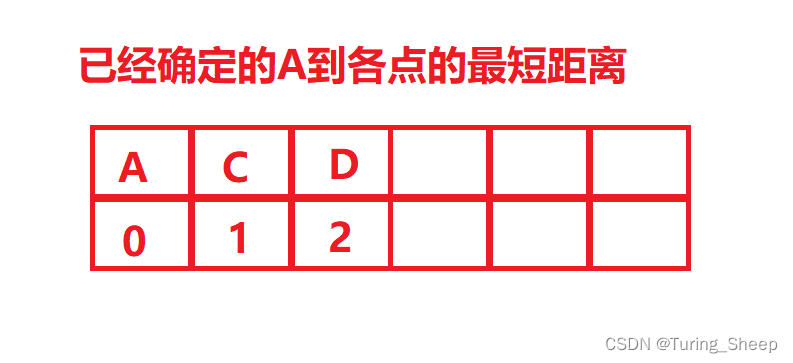
除了挑出最短路D之外，我们发现，以C为中转站的方式去走，各个点到A的距离都变小了。所以更新一下上表。

当我们知道了D点的最短路后，我们能不能再用结论1，尝试着再去更新一下最短路呢？

好，那我们再看一下以D为中转站，去找一下其邻接点到A的距离。

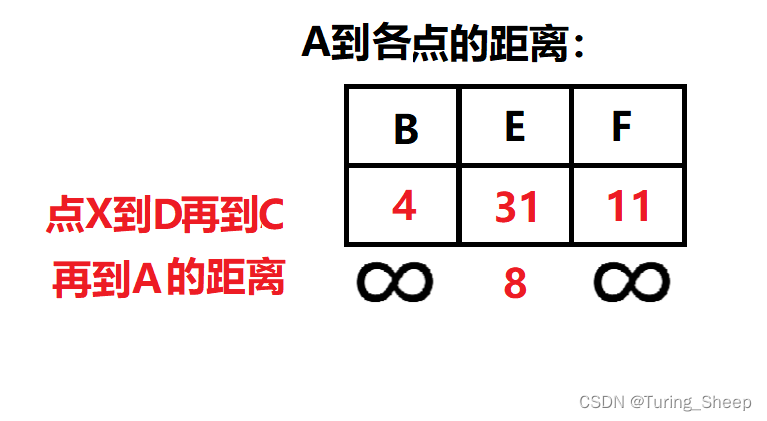
惊喜的是，我们的E点通过当前路线，的确小于了之前，但是另外两个点都比之前远了，其中一个原因就是B和F与D不连通。

那么我们来分析一下上下的两行数字：

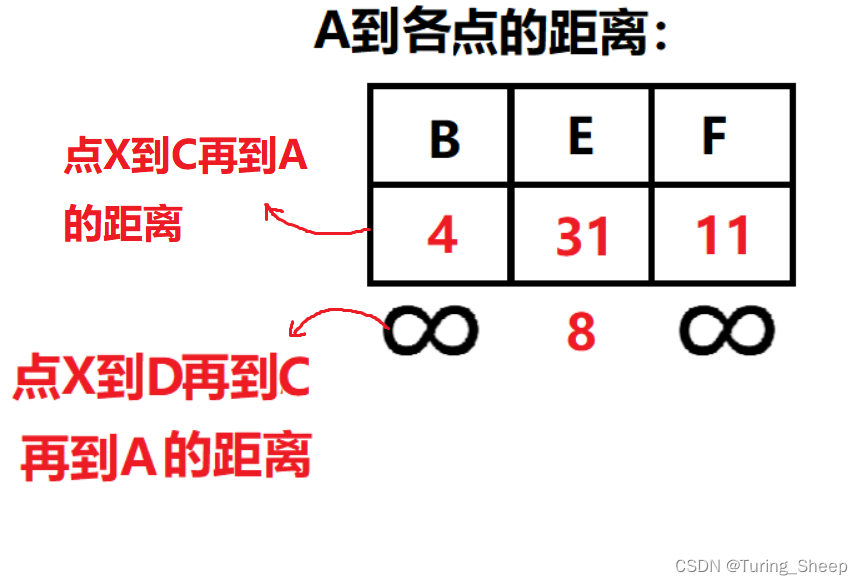
第一行的走法是：X—>C—>A。但是XC不是最短的，因为最短的DC所在的D点已经选出去了。也就是说第一行都不满足我们的结论1。
因此，我们无法保证上面的是最短路。

第二行的走法是：X–>（D–>C–>A），根据结论1：这种走法是在**必须经过4个节点的情况下，最短的距离。**我们肯定能保证（D–>C–>A）小于X—>C—>A。但是，我们再给前面加上一个X–>D的距离呢？答案肯定是不一定的。

因此，在这种情况下，我们只能通过对比的方式去对比表中的情况。

从而得到了以下的结果。

为什么黑框中最小的就是确定的最短路呢？。这是不是类似于我们的结论2的思路？

我们仔细观察会发现，列表中是所有能到A的点，而表中的数字是，不通过其他黑色的点，通过一系列已知的中间点，或者直接抵达的方式所得到的距离。

如果这个距离不是最短的，那么他必须经过表中的其他点，再到A点。由于再到A点的过程的距离已经大于了我们直接到的距离，所以再加上一个该点到表中某点的距离更是大于了直接抵达的距离。

因此，表格中最小的那个数，就是那个点到A点的最短路！！

而上述的思路，就是我们证明结论2的思路。

所以我们可以将表格中的点看作A的邻接点！！然后选最小的，利用结论2。

此时我们将B拿出来：

此时，我们再看看通过某个点X到B再到A的距离是否会小于表中的数据，然后选出最小的，再放在红表中。然后再重复这个过程。

所以该算法的所有步骤如下：

不断地找邻接点，以最近的邻接点为中间点，去继续寻找新的路线，然后更新黑表，选出黑表中最小的放到红表中，最后这个红表就是所有点的最短路。

（3）算法的本质思想：

Dijkstra算法本质是一种贪心策略，即我每次都优先选择对于当前的情况最好的选择。
比如我们每次都尝试着在找到最短路的基础上，去找其他的路。即每次都做对当下最好的选择。

三、Dijkstra的实现

1、问题：

2、代码模板：

#include<iostream>
#include<cstring>
using namespace std;
const int N=510;
int g[N][N],dis[N];
bool s[N];
int n,m,a,b,c;
int dijkstra()
{
    memset(dis,0x3f,sizeof dis);
    dis[1]=0;
    for(int i=1;i<=n;i++)
    { 
        int t=-1;
        //结论2：
        for(int j=1;j<=n;j++)
        {
            if(!s[j]&&(t==-1||dis[j]<dis[t]))t=j;
        }
        s[t]=true;
        
        //结论1：
        for(int j=1;j<=n;j++)
        {
            dis[j]=min(dis[j],g[t][j]+dis[t]);
        }
    }
    if(dis[n]==0x3f3f3f3f)return -1;
    else return dis[n];
}
int main()
{
    memset(g,0x3f,sizeof g);
    scanf("%d%d",&n,&m);
    while(m--)
    {
        scanf("%d%d%d",&a,&b,&c);
        g[a][b]=min(g[a][b],c);
    }
    cout<<dijkstra();
}

3、代码分析：

4、问题解决：

（1）为什么用邻接矩阵

邻接矩阵是一个二维数组，他记录了所有可能存在的边，当边数较少的时候，它会存储很多没用的点。但是现在我们发现边的数量是10的5次方。所以基本上每两个点之间都有边，所以用邻接矩阵几乎不会浪费空间。

四、复杂度分析：

外循环n次，内循环2*n次，所以时间复杂度是O(N²)