正数的反码是其本身
负数的补码是其反码+1
原码 十进制数据的二进制表现形式 byte b = 13 1101(13的十进制)byte代表占存储的一个字节(1字节等于8位) 此时13的在存储里的形式 0000 1101 (原码最左边0为正,1为负 ,所以只有7位代表数字本身)
浮点型
0.3 ,+100.8,-8.9,-6319.0
声明关键字 float(单精度) double(精度是float的两倍)
关注重点在于精度
double使用较多
float的小数点七位之后精度会被丢失
deuble不会丢失
小数 二进制和十进制转换
十进制转换位二进制
用十进制的小数部分乘以2,取整;再用剩下的小数部分乘以2,取整,直到取整之后剩下的小数部分位
0.5十进制转换位二进制
0.5 * 2 = 1 0.1
0.25 * 2 = 0.5 * 2 = 1.0 0.01
0.2 0. 0.0 0.01 0.011
0.2 * 2 =》 0.4 * 2 =》 0.8 * 2=》 1.6 =》 0.6 * 2=》1.2

二进制转换为十进制(小数)
使用二进制的小数的每一位上的数,乘以2的若干次方(从小数点后的第一位开始-1,-2,-3) ,然后将所有乘积相加
二进制0.1转换为10进制
公式
a^-n = a^ 分之 1
0.1 =》 1 *2^-1 1 * 0.5 = 0.5 2的负一次方为0.5
0.6=》6 * 2^-1 6 * 0.5 => 3
6* 2分之一(0.5) + 3 * 4分之一(0.75)
0.63 =》6 * 2^-1 + 3*2^-2 3+ 3*0.25 = 3.78
doubl精度丢失问题(double类型-保留14位?-15位)
内存中一部分存整数 一部分存点 一部分存浮点数 但是内容是有限的,小数循环,存不下
精度丢失-----小数转换为二进制,尾部无线循环,内存有限只能保存一部分,导致精度丢失
float(只保留7位精度)


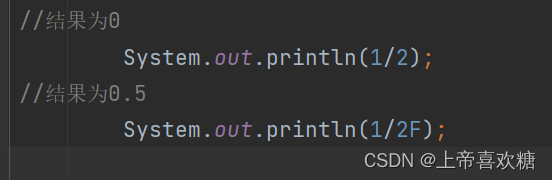
在Java中,1和2都是整数(int类型),因此1/2会执行整数除法并返回整数结果。这意味着结果会被截断为0,因为1除以2得到的值小于1。如果您希望得到浮点除法的结果,可以将至少一个操作数强制转换为浮点数。例如,将1除以2.0会得到0.5作为double类型的结果。
1/2.0 默认返回结果为double类型浮点数
1/2.0F 返回结果为float 类型
与或非 --- 逻辑短路
&& 找假 短路 左侧第一个为假,即为假,不判断右侧
|| 找真 短路 左侧第一个为真。即为真。不判断右侧
! 取反
+= 加等于
-= 减等于
*= 乘等于
/= 除等于
%= 取余等于
三元运算
Int a = true ? “1” : ‘’2‘’
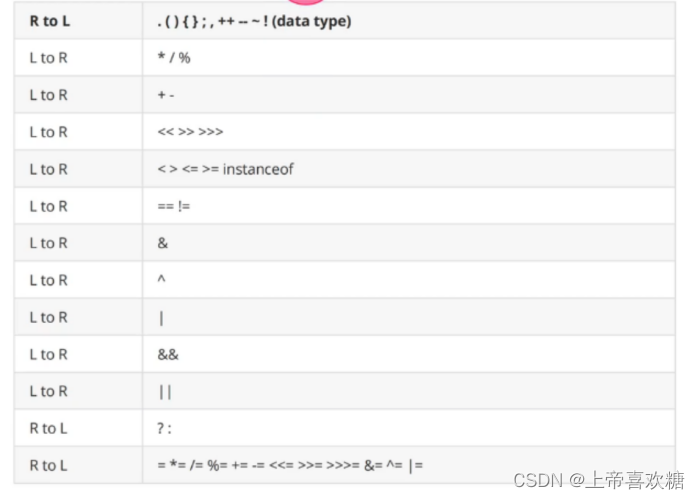
优先级
自增 自减 > 算术 > 比较运算(大于小于 比等(==)和不等(!=)的优先级高)> 逻辑运算符 > 三元运算符 > 赋值运算
逻辑的 && 优先级高于 ||
Boolean = 3 + 5 > 1 || 6 /3 == 1 && 100 < 10 不确定的时候使用小括号包裹提升优先级