1. 从传统机器学习到元学习

传统的机器学中，我们选择一个算法�F，把数据放进去，学出来一组参数�θ，在测试数据上用，得出结果。如图：

基于这种思想，我们能不能学�F呢？

当然可以了！现在我们的目标就是去学习�F

如上图，A就是元学习算法，�ω就是算法中可学的参数，称为元知识，得到最适用的�F之后，再把数据放进去，得到�f，最终输出结果.

那现在有个问题了

上述图中只有一个任务，就是分清楚猫还是狗，那遇到多任务时，该怎么办？就是让算法不仅仅可以分猫狗，还能分苹果橘子，自行车和汽车等。如下图所示：

如果让�F都能做，这时，�ω就是对所有分类任务都比较好的算法，得到后，可以让他做新的任务，分手机和电脑，得到模型��fθ，这时该模型就有分辨手机和电脑的能力了。

单任务元学习目标是找到一个最适合该任务的算法，而多任务元学习是找到最适合所有任务的算法，并且这个算法能够处理新的任务。

1.1 怎么学算法参数�ω 呢？

传统的机器学习如何学习参数�θ呢？

如下图，先建立一个模型，把“猫”输入，不断进行反馈；

第二步定义损失函数，如下图，用交叉熵来定义，也就是说通过预测的概率和真实的标签对比，预测的概率越低，分类越错，惩罚就越高，惩罚越高的话，下一次分错的概率就越低，通过这样的方式学习。

最后把损失加起来得到总的损失，求梯度，目的是让他下一次不要犯错了，根据不断的优化迭代，得到�∗θ∗，这就是学出来的模型参数。

上述步骤是求模型的参数，那么算法的参数怎么学呢？

其实和求模型的参数一模一样，本质没有区别

因为模型的参数是想要让它在数据上更通用更一般化，在元学习里，只不过是把上述的数据换成了任务，使其在没见过的任务上也做的好，怎么做呢？如下图

给出task1,task2,得到初始化算法��Fω，根据��Fω测试，得到损失，然后加起来，得到最终损失�(�)L(ϕ) 。

与传统就机器学习相比，传统的机器学习损失是在训练样本上做的，而元学习是在测试样本做的。但是机器学习中不可以用测试数据用于训练，怎么办？

将训练数据分为支撑集（Support set）（优化模型参数�θ）和查询集（Query set）（优化算法参数�ω，如果�ω不好，那�θ也一定不好）。对于测试数据，也同样分为支撑集和查询集，但是测试数据的查询集不参与学习

那么它的流程是什么样的呢？如下：

先有一个元学习算法，元学习算法给你一个支撑集之后，会得到一个通用的模型，这个模型在查询集上评估一下，看看好不好，最后得到一个�ω，再用这个算法在测试集上的支撑集上更新，得到一个模型，再用这个模型，在查询集上做最终的预测。

训练和测试集在元学习中称为元训练和元测试。公式表示如下：

元训练：

如上图，它分为内层和外层优化，外层用于学算法参数，内层用于学模型参数，内层是给出�ω学出�∗θ∗，把�∗θ∗拿到查询集中，验证学的怎么样，如果不好，说明�ω不好，通过loss去更新�∗ω∗，不断迭代。

元测试：

已经学到最好的算法后，在测试集的支撑集上去学一个模型，最终，�∗θ∗就是测试模型。

这个元知识可以是什么呢？ 可以使非常多的东西，例如：超参数，初始化的模型参数，embeddings,模型架构，损失函数等等。

2.元学习的分类

从方法论角度，元学习分为三类：基于优化，基于模型，基于度量。

展开讲讲

2.1 基于优化的元学习

�ω在优化的过程中起作用，它指导你去优化，告诉你当前该用什么优化器，相关的一篇论文如下：

[1606.04474] Learning to learn by gradient descent by gradient descent (arxiv.org)

论文题目为：用梯度下降的方式去学习如何用梯度下降学习

在元学习中，通过元知识�ω学习合适的优化函数，公式如下：

一个典型的基于优化的方法是MAML(Model-Agnostic Meta-Learning)：

我们定义初始化参数为�θ，定义在第n个测试任务上训练之后的模型参数为�^�θ^n，于是总的损失函数为�(�)=∑�=1��(�^�)L(ϕ)=∑n=1Nln(θ^n)，pre-training的损失函数是�(�)=∑�=1��(�)L(ϕ)=∑n=1Nln(ϕ)，直观上理解是MAML所评测的损失是在任务训练之后的测试loss，而pre-training是直接在原有基础上求损失没有经过训练。

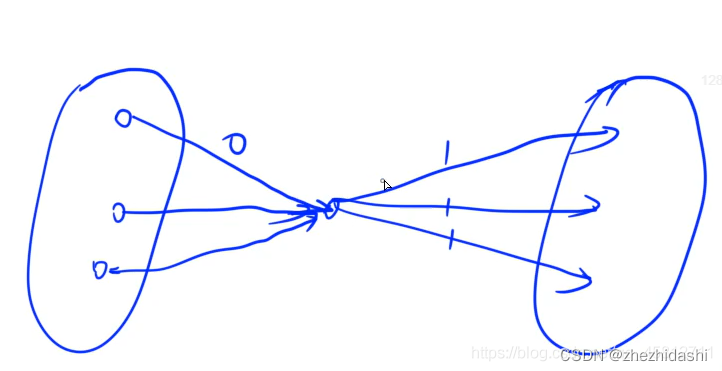
李宏毅老师举了一个非常形象的例子，假设模型参数的�ϕ和�θ向量都是一维的，MAML的初衷是找到一个不偏不倚的�ϕ，使得不管是在任务1的loss曲线�1l1还是任务2的loss曲线�2l2上，都能下降到分别的全局最优。

而model pre-training的初衷是寻找一个从一开始就让所有任务的损失之和处于最小状态�ϕ，它并不保证所有任务都能训练到最好的�^�θ^n，如上图所示，�2l2即收敛到局部最优。接下来李老师还做了一个很现实的比喻，他把MAML比作选择读博，意味着在意的是以后的表现如何，即潜力；而model pre-training就相当于选择毕业直接去互联网大厂工作，马上就把所学技能兑现金钱，在意的是当下表现如何。

总结起来，MAML算法的框架其实很简单，值得注意的是两个学习率�ϵ和�η所用的地方不同：