STL之Stack与queue的模拟实现与duque的底层结构
文章目录
- STL之Stack与queue的模拟实现与duque的底层结构
- 设计模式的概念
- 适配器模式
- stack的实现
- queue的实现
- 双端队列——deque
- deque的底层结构
设计模式的概念
设计模式像是古代的兵法,是以前的人总结出来的一些在特定的情况下,某种特定的好用的方法总结
STL中迭代器也是一种设计模式——迭代器模式
STL中stack和queue的实现就是使用了一种设计模式——适配器模式!
适配器模式
那么什么叫做适配器模式呢?现实中什么东西可以被叫做适配器?
例如手机充电头!——就是一种电源适配器!我们日常的电源一般都是220v,但是手机一般的充电功率都是几v!如果不使用电源适配器,那么直接充电很容易会让手机坏掉!
所以适配器模式是什么?适配器模式就是一种转换!用已有的东西转换出我们现在想要的东西!
上面提到的迭代器模式就是不暴露底层细节,封装后提供同一的方式来访问容器
如果我们使用适配器模式,我们去手动实现一个stack和queue,那么我们就要从头开始进行设计
//例如 template<class T> class Stack { public: //里面实现各种函数 private: T* _a; size_t _size; size_t capacity; }但是我们其实没有必要做那么多重复的工作!vector已经帮我们实现了很多我们必要的东西!我们可以通过适配器模式的思想将vector转换为stack!(list也可以)
stack的实现
#include <vector> #include <list> namespace MySTL { template<class T, class Container = std::vector<T>> class stack { public: void push(const T& x) { _con.push_back(x); } void pop() { _con.pop_back(); } bool empty() { return _con.empty(); } const T& top() { return _con.back(); } size_t size() { return _con.size(); } private: Container _con; }; } //test.cpp //测试代码 int main() { MySTL::stack<int, vector<int>> s1; //MySTL::stack<int, list<int>> s1; s1.push(1); s1.push(2); s1.push(3); s1.push(4); s1.push(5); while (!s1.empty()) { cout << s1.top() << " "; s1.pop(); } cout << endl; return 0; }Container 这个模板参数的意义就在于能够让我们哦stack更加的灵活!因为无论是vector实现的栈和list实现的栈都有各自的优点!都难以互相代替!既然如此就将其写成一个模板参数!需要的时候就替换!
我们可以给这个模板参数一个缺省值默认是vector,想要的适合再进行替换!
queue的实现
#include<list>
#include<vector>
namespace MySTL
{
template<class T,class Container = std::list<T>>
class queue
{
public:
void push(const T& x)
{
_con.push_back(x);//尾插
}
void pop()
{
_con.pop_front();//头删
}
bool empty()
{
return _con.empty();
}
const T& front()//获取头元素
{
return _con.front();
}
const T& back()//获取尾元素
{
return _con.back();
}
size_t size()
{
return _con.size();
}
private:
Container _con;
};
}
//test.cpp
#include "queue.h"
int main()
{
MySTL::queue<int> s1;
//MySTL::queue<int,list<int>> s1;
//MySTL::queue<int,vector<int>> s1;
s1.push(1);
s1.push(2);
s1.push(3);
s1.push(4);
s1.push(5);
while (!s1.empty())
{
cout << s1.front() << " ";
s1.pop();
}
cout << endl;
return 0;
}
MySTL::queue<int,vector<int>> s1;这个使用vector的时候,使用pop的会报错!因为vector是不支持pop_front!
也不提倡使用vector作为队列的底层!因为这样子头删的效率会很低!是O(N)
stack和queue虽然说是容器!但是准确的说是容器适配器!——是用容器适配转换出来的!
双端队列——deque
我们可以看到库里面的stack和queue全部的默认容器其实不是list和vector!而是deque——这是双端队列!
为什么是用deque这个容器呢?——这就不得不提到vector和list的缺点了!
vector缺点
- 头部,中部插入删除的效率低
- 扩容存在消耗
- 不支持头删!——pop_front ,也就是说不支持队列!
list缺点
- 不支持随机访问!
- CPU高速缓存的命中率低!
所以为了兼具list和vector的优点,于是有了双端队列这一个数据结构!
兼具这list和vector的所有操作!有着list和vector的优点!既可以头插头删,又可以随机访问!
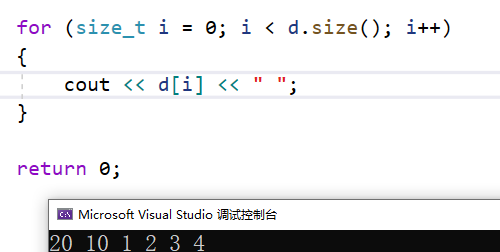
#include<deque> #include<iostream> using namespace std; int main() { deque <int> d; d.push_back(1); d.push_back(2); d.push_back(3); d.push_back(4); d.push_front(10); d.push_front(20); for (size_t i = 0; i < d.size(); i++) { cout << d[i] << " "; } return 0; }
看起来deque十分的完美?但是真的是这样吗?
其实不是的!如果deque真的那么的完美,那么vector和list就不需要存在了!
deque的底层结构
这里我们简单的介绍一下deque的底层结构!
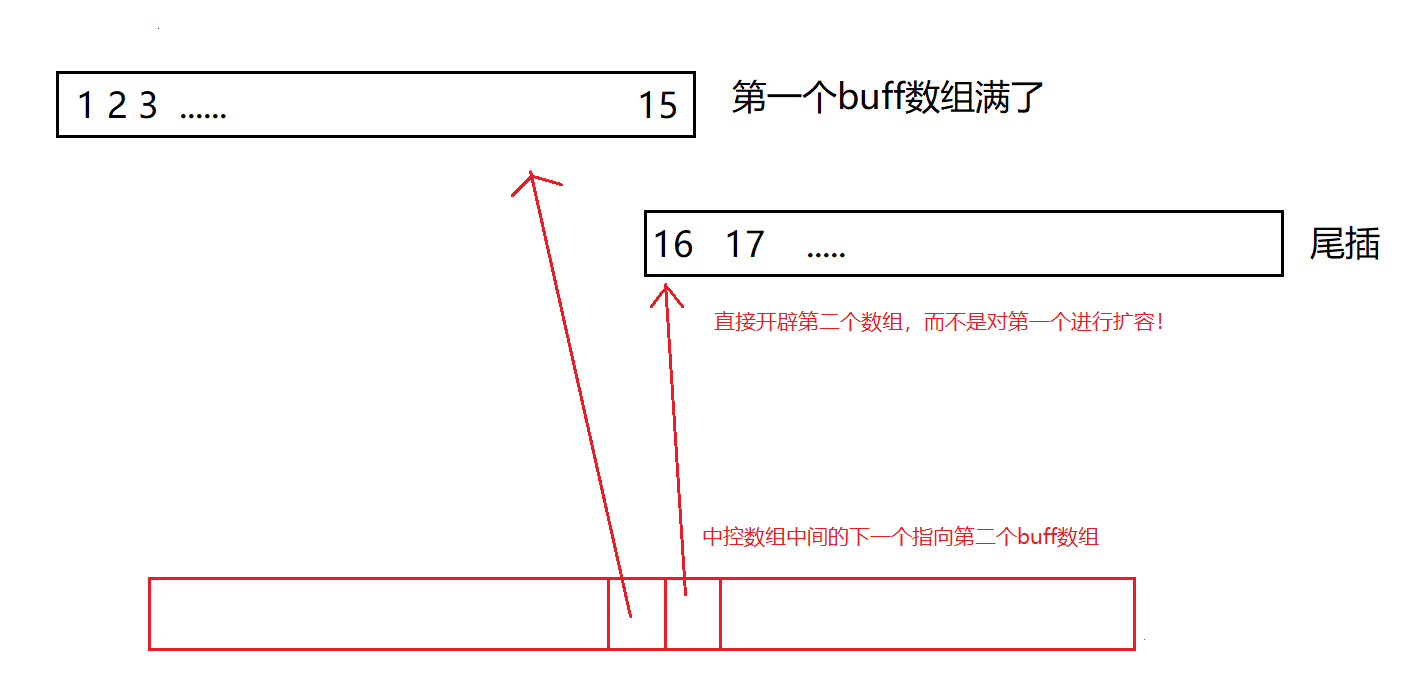
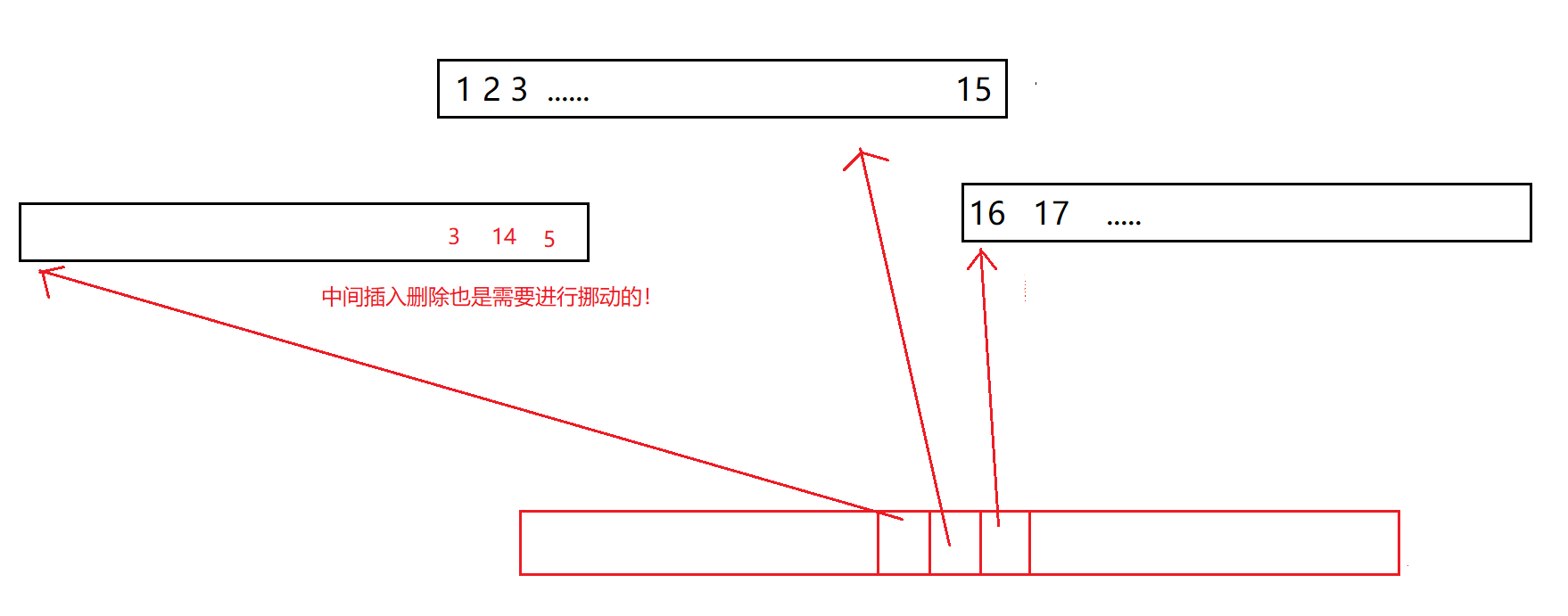
deque是由多个buff数组构成的!——而由一个==中控数组(指针数组)==来管理所有的buff数组
等一个buff数组满了之后,如果对于一般的vector,就应该开始扩容,但是对于deque,不会进行扩容,而是开第二个buff数组
第二个buff满了就开下一个,直到中控数组的也满了之后!才需要对中控数组进行扩容!
上面的插入操作都是尾插!
如果要进行头插呢?——是要挪动位置吗?不是!而是也是新开一个数组!
头插插入那个buff数组最右边开始!
这样子设计,它的CPU缓冲区命中率也可以,头插效率也不错!——虽然看上去也会有空间浪费!但是其实buff数组一般都比较小,相比vector一次性二倍扩或者1.5倍扩,造成的浪费是可以接受的!
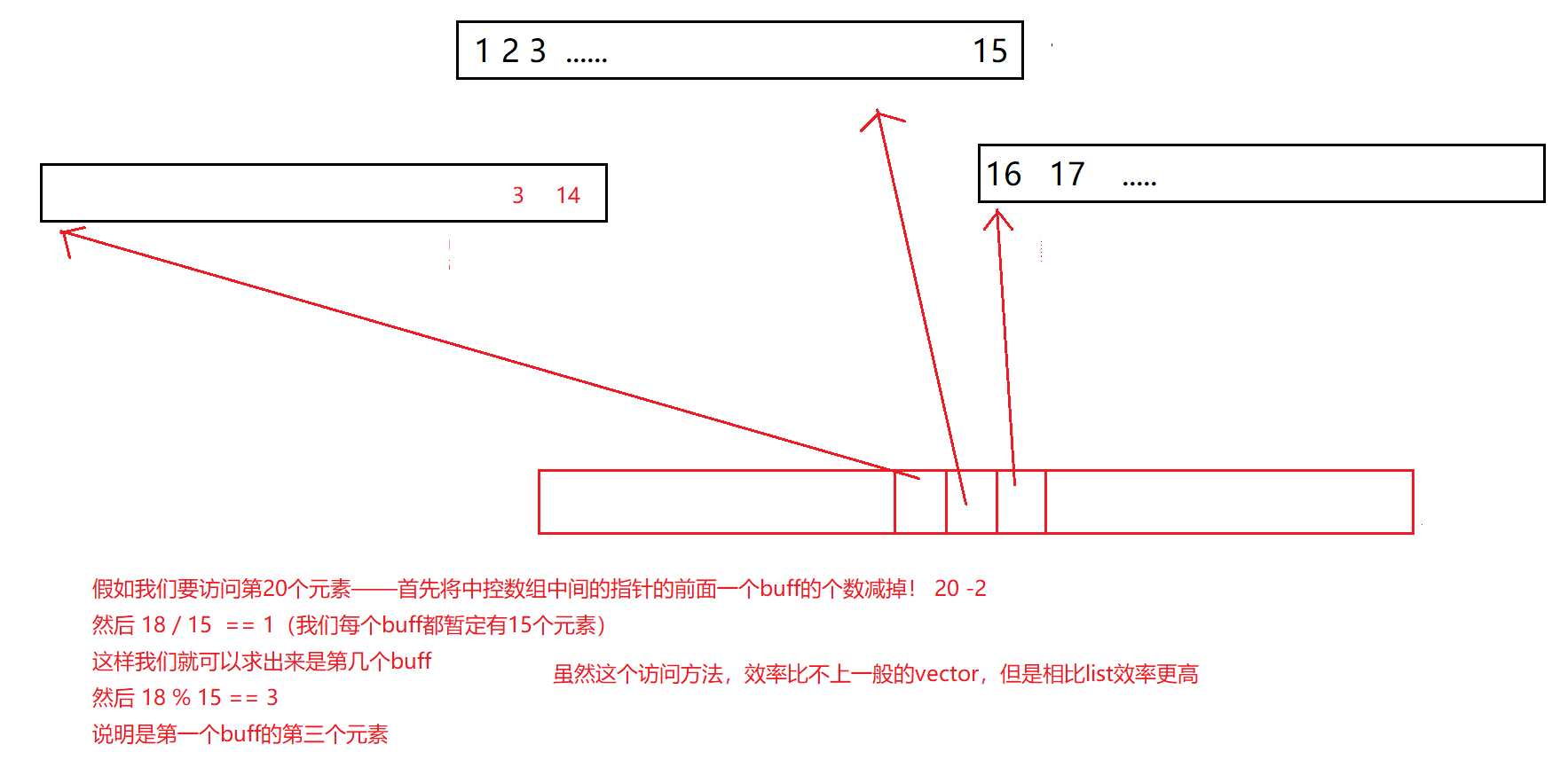
那么这个deque的随机访问是如何实现的?
这也是deque的第一个问题,随机访问有一定的消耗!没有vector的随机访问效率高——但是比起list的每一次都要遍历查找效率又高很多!
那么我们还有个问题,如果我们想要在14的后面进行插入一个5要怎么办?——答案是要进行挪动!
所以这既是deque的第二个问题,对于中间的插入和删除也存在一定消耗! 没有list的中间插入删除效率高——但是又相比vector每一次的中间插入删除都要大部分挪动,效率又更高!因为只要挪动一小部分!
所以deque是一个折中的一种方案!所以这就是为什么它被使用与stack和queue的默认容器!相比vector没有扩容,相比list高速缓存命中率也不错!
中间插入删除少,头插头删,尾插尾删多,偶尔随机下标访问的时候使用deque是不错的!
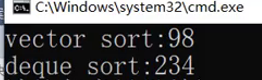
但是如果要大量的进行随机访问或者进行排序还是得使用vector!
有差不多两倍的性能差距!
如果要大量的中间插入删除还是得使用list
因为deque的模拟实现十分的复杂,我们这里就不进行模拟实现了!
如果有兴趣读者可以看《STL源码剖析》这本书去深入钻研