题目链接

从前序与中序遍历序列构造二叉树

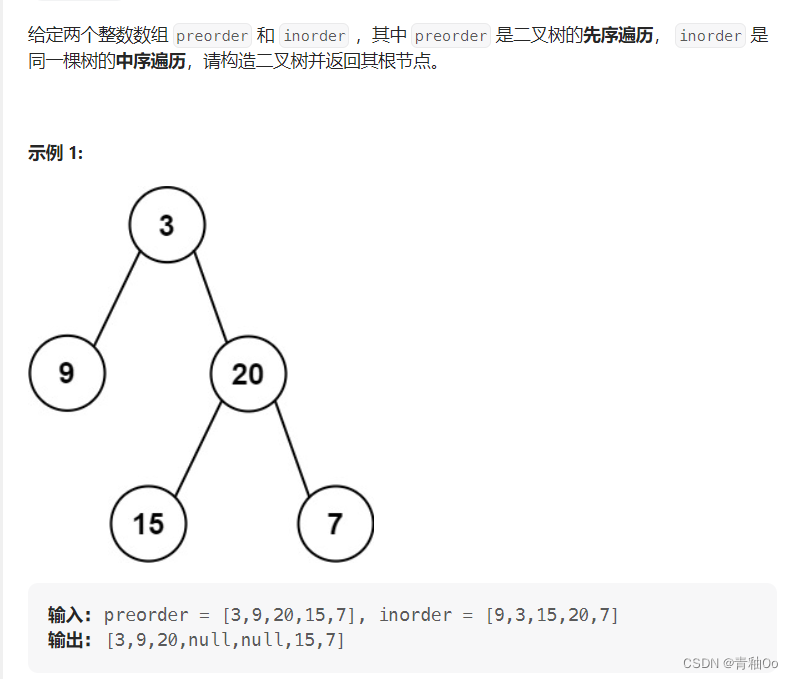
题目描述

注意点

• inorder.length == preorder.length
• preorder 和 inorder 均 无重复 元素
• inorder 均出现在 preorder
• preorder 保证 为二叉树的前序遍历序列
• inorder 保证 为二叉树的中序遍历序列

解答思路

• 前序遍历的首个节点为根节点，可以根据根节点在中序遍历中的位置找到哪些节点属于左子树，哪些节点属于右子树
• 如果每次都根据根节点的值在中序遍历中去查找位置，则会增加时间的开销，所以可以将中序遍历中的节点值及其在中序遍历中的位置存储到一个哈希表中，每次查找位置只需要花费O(1)的时间，以空间换时间
• 通过递归的方法不断寻找每个子树的根节点及其左右子树，为了方便寻找，每次递归时需要传入preorder_left, preorder_right, inorder_left, inorder_right，其中preorder_left是当前子树在前序遍历中的第一个节点，也就是根节点，根据根节点在中序遍历中的位置可以与inorder_left推出其左子树的节点数量size，在此基础上可以继续递归推出该子树的左右子树

代码

class Solution {
    // 存储中序遍历关系映射
    Map<Integer, Integer> map;

    public TreeNode buildTree(int[] preorder, int[] inorder) {
        int n = inorder.length;
        map = new HashMap<>(n);
        for (int i = 0; i < n; i++) {
            map.put(inorder[i], i);
        }
        return buildMyTree(preorder, inorder, 0, n - 1, 0, n - 1);
    }

    public TreeNode buildMyTree(int[] preorder, int[] inorder, int preorder_left, int preorder_right, int inorder_left, int inorder_right) {
        // 没有元素无法构成树
        if (preorder_left > preorder_right) {
            return null;
        }
        TreeNode root = new TreeNode();
        // 此时先序遍历左侧为根节点
        root.val = preorder[preorder_left];
        // 该树左子树的节点数量
        int size = map.get(root.val) - inorder_left;
        root.left = buildMyTree(preorder, inorder, preorder_left + 1, preorder_left + size, inorder_left, inorder_left + size);
        root.right = buildMyTree(preorder, inorder, preorder_left + size + 1, preorder_right, inorder_left + size + 1, inorder_right);
        return root;
    }
}

关键点

• 理解前序遍历和中序遍历
• 在每次递归左右子树时，理解应该怎样传入preorder_left, preorder_right, inorder_left, inorder_right四个值
• 对于左子树，因为此时preorder_left已经作为根节点，所以传入preorder_left需要加1，preorder_right为preorder_left + size，inorder_left为inorder_left，inorder_right为inorder_left + size
• 对于右子树，preorder_left为preorder_left + size + 1，preorder_right为preorder_right，因为此时inorder_left + size已经作为根节点，所以inorder_left为inorder_left + size + 1，inorder_right为inorder_right