小朋友们好,大朋友们好!
我是猫妹,一名爱上Python编程的小学生。
和猫妹学Python,一起趣味学编程。
今日主题
咱们今天的内容比较抽象,也比较有趣。
这里的图是指计算机中的图,确切地说,是一种数据结构。
在解决实际问题时,经常会用到。
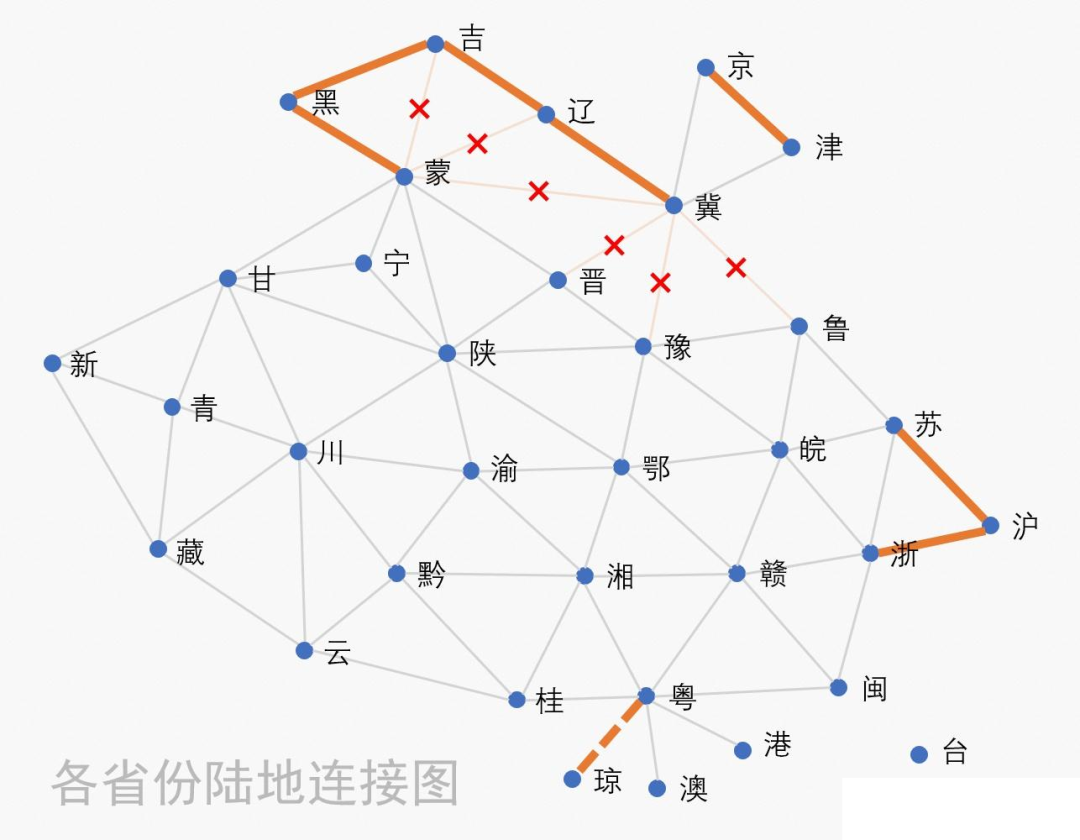
我们举个生活中的例子:
一个人要把大陆31个省会城市自驾游一遍,最短路径是多少公里?
一个人能在一个省份只经过一次的情况下把大陆31个省会城市自驾游一遍吗?



今天的主题有:
图的定义
图的分类
图的接口
图的Python表示
图的定义
图G由两个集合组成,顶点集合和边集合。
一个由顶点(vertex)构成的有穷非空集合和一个由边(edge)构成的有穷允空集合。
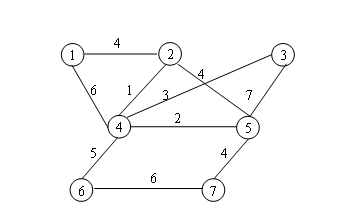
比如上图:
顶点集合有:1,2,3,4,5,6,7
边集合有:有10条,带权值
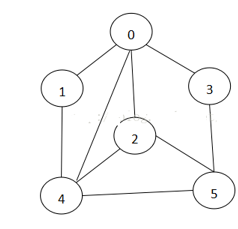
比如上图:
顶点结合有:0,1,2,3,4,5
边集合有:共9条,不带权值
图的分类
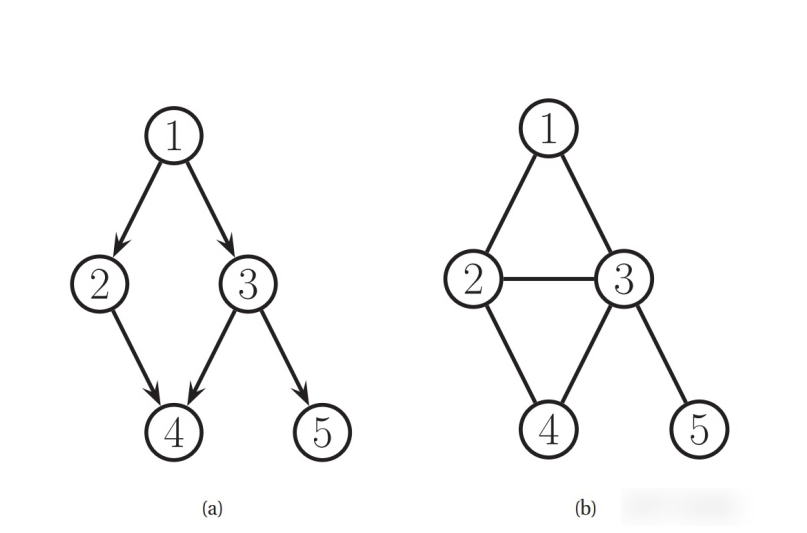
图根据边是否有方向,分为有向图和无向图。
(a)为有向图,(b)为无向图
图根据边是否有权值,分为边无权值的图,边有权值的图。
如下图:

节点的度
无向图中结点的度:顶点引出的边数和。
有向图中结点的度:分为入度和出度。入度为指向该顶点的边数和,出度为该顶点向外指向的边数和。
图的接口
addVertex(v)添加顶点
deleteVertex(v)删除顶点
vertexes(v)获取所有顶点
addEdge(v1,v2)添加一条边
deleteEdge(v1,v2)删除一条边
edges()获取所有边
adjacent(v)获取v的所有邻接顶点
isEmpty()判断图是否为空
Python中的图
可以使用Python自带的列表、集合、字典来表示图,也可以使用第三方库networkx。
可以使用邻接矩阵、邻接列表、邻接集合、邻接加权字典来表示图。%3CmxGraphModel%3E%3Croot%3E%3CmxCell%20id%3D%220%22%2F%3E%3CmxCell%20id%3D%221%22%20parent%3D%220%22%2F%3E%3CmxCell%20id%3D%222%22%20value%3D%22b%22%20style%3D%22ellipse%3BwhiteSpace%3Dwrap%3Bhtml%3D1%3Baspect%3Dfixed%3BfillColor%3D%2360a917%3BfontColor%3D%23ffffff%3BstrokeColor%3D%232D7600%3B%22%20vertex%3D%221%22%20parent%3D%221%22%3E%3CmxGeometry%20x%3D%22350%22%20y%3D%22130%22%20width%3D%2220%22%20height%3D%2220%22%20as%3D%22geometry%22%2F%3E%3C%2FmxCell%3E%3C%2Froot%3E%3C%2FmxGraphModel%3E
邻接矩阵
设无向图G=(V,E),其中顶点集V=v1,v2,…,vn,边集 E=e1,e2,…,eε。用aij表示顶点vi与顶点vj之间的边数,可能取值为0,1,2,…,称所得矩阵A=A(G)=(aij)n×n为图G的邻接矩阵。
邻接矩阵可以描述有向图和无向图。


邻接矩阵的存储特点:
(a)无向图的邻接矩阵是一个对称矩阵,有向图不一定是。
(b)邻接矩阵所需的存储空间值域只与顶点数有关系。
(c)用邻接矩阵存储图,容易判断两个点之间是否有边。
(d)如果一个有向图的邻接矩阵为三角矩阵(主对角线为0),则它的拓扑排序一定存在。
(e)小技巧:
无向图:邻接矩阵的第i行或者第i列的非零元素的个数正好是第i个顶点Vi的度;
有向图:邻接矩阵的第i行的非零元素个数正好是第i个顶点Vi的出度,第i列非零元素的个数正好是第i个顶点Vi的入度。
(f)邻接矩阵也可以表示有权值的图,此时单元格内容是边的权值。
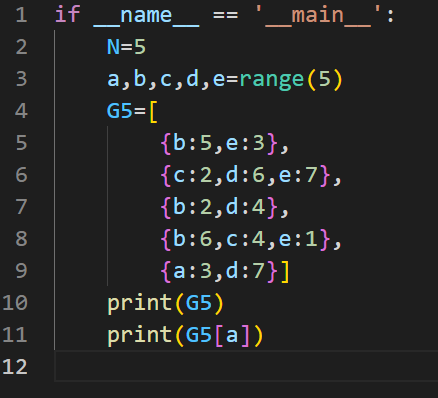
上图Python代码参考:


邻接矩阵的缺点:
-
当结点很多,边很少时,很多个0,浪费空间。
-
寻找每个结点的邻接顶点时,需要遍历列表,稍有不便。
邻接集合
只存储有边的数据,不存储无边的数据。
比如上图中,和a相邻的边,只存储ad和ae,只需要存储和a相邻的结点是d和e就可以了。


邻接列表
和邻接集合类似,只是将集合变为列表。
邻接加权字典

可以使用邻接加权字典表示有权值的图。
好了,我们今天的学习就先到这里。
你学会了吗?

好了,我们今天就学到这里吧!
如果遇到什么问题,咱们多多交流,共同解决。
我是猫妹,咱们下次见!