动态规划

• 01背包求方案
• 这里跑一边dp。如果要满足字典序最小的话，可以用贪心法。从1~N的物品，可选可不选的情况下要选上。
• 第一遍跑dp要从N到1，这样子最终的答案保存在了$f(1,V)$里面，然后第二次输出方案的时候就可以从1~N输出了。第一遍从1到N跑dp的话，还真是不好设计。

#include<cstdio>
#include<algorithm>
using namespace std;
const int maxn = 1010;
int f[maxn][maxn], v[maxn], w[maxn], N, V;
int main() {
	scanf("%d%d", &N, &V);
	for (int i = 1; i <= N; i++) scanf("%d%d", &v[i], &w[i]);
	for (int i = N; i >= 1; i--) {
	    //注意这里从小到大循环并不是完全背包。因为这个是二维数组，不是一维数组。
		for (int j = 0; j <= V; j++) {
			f[i][j] = f[i + 1][j];
			if (j >= v[i]) f[i][j] = max(f[i][j], f[i + 1][j - v[i]] + w[i]);
		}
	}
	int j = V;
	for (int i = 1; i <= N; i++) {
		if (j >= v[i] && f[i + 1][j - v[i]] + w[i] == f[i][j]) {
			printf("%d ", i);
			j -= v[i];
		}
	}
	return 0;
}

题意：第 $i$ 种物品最多有 $s_i$ 件，每件体积是 $v_i$，价值是 $w_i$。

• 题意：有 $N$ 组物品和一个容量是 $V$ 的背包. 每组物品有若干个，同一组内的物品最多只能选一个. 每件物品的体积是 $v_{ij}$，价值是 $w_{ij}$，其中 $i$ 是组号，$j$ 是组内编号.

#include<cstdio>
#include<algorithm>
using namespace std;
const int maxn = 110, maxv = 110;
int v[maxn][maxn], w[maxn][maxn], f[maxv], s[maxn];
int N, V;
int main() {
	scanf("%d%d", &N, &V);
	for (int i = 1; i <= N; i++) {
		scanf("%d", &s[i]);
		for (int j = 0; j < s[i]; j++) {
			scanf("%d%d", &v[i][j], &w[i][j]);
		}
	}
//其实这个和01背包的思路差不多，但是一定不要把第二重和第三重循环反过来。如果反过来的话，不能保证每组只选一个物品。
	for (int i = 1; i <= N; i++) {
		for (int j = V; j >= 0; j--) {
			for (int k = 0; k < s[i]; k++) {
				if (j >= v[i][k]) f[j] = max(f[j], f[j - v[i][k]] + w[i][k]);
			}
		}
	}
	printf("%d\n", f[V]);
	return 0;
}

• 二维费用背包问题。
• 就是说有 $n$ 个物品，手里有两种容量 $V_1,V_2$，每选择一个物品，占据的第一种容量为 $v_1$，占据第二种容量为 $v_2$.
• 体积是二维的。也就是说皮卡丘抓小精灵，小精灵既会造成伤害又会消耗精灵球。问最多能抓多少只小精灵，而抓的小精灵数量相同的时候，最少消耗多少 $HP$？
• $f(i,j,k)$：表示从前 $i$ 个物品中挑选，费用 $1$ 花费不超过 $j$，费用 $2$ 花费不超过 $k$，物品价值的最大值。
• 对于这道题，压缩到二维之后，由于皮卡丘的 $HP$ 不可以为 $0$，因此答案是 $f(V1,V2-1)$.

#include<cstdio>
#include<algorithm>
using namespace std;
const int maxn = 1010, maxm = 510, maxk = 110;
int v1[maxk], v2[maxk], f[maxn][maxm], V1, V2, N;
int main() {
	scanf("%d%d%d", &V1, &V2, &N);
	for (int i = 1; i <= N; i++) scanf("%d%d", &v1[i], &v2[i]);
	for (int i = 1; i <= N; i++) {
		for (int j = V1; j >= v1[i]; j--) {
			for (int k = V2; k >= v2[i]; k--) {
				f[j][k] = max(f[j][k], f[j - v1[i]][k - v2[i]] + 1);
			}
		}
	}
	int ans1 = f[V1][V2 - 1], ans2 = V2;
	for (int j = 0; j <= V2 - 1; j++) {
		if (f[V1][j] == ans1) {
			ans2 = j; break;
		}
	}
	printf("%d %d\n", ans1, V2 - ans2);
	return 0;
}

• 二维费用求最小值.
• 体积：一共有 $k$ 种 物品，对于第 $i$ 种物品，第一维费用是 $v_{1i}$，第二维费用是 $v_{2i}$，价值 是 $w_i$，每个物品至多被选一次。求一个选择方案，使得第一维费用不少于 $n$，第二维费用不少于 $m$ 且 总价值最小
• 这道题有所改变，$f(i,j,k)$表示选前 $i$ 个物品，费用 $1$ 不少于 $j$，费用 $2$ 不少于 $k$.
• 由于 $j$ 和 $k$ 是负数时，$f(i,j,k)=0$，因此这个状态和 $0$ 等效，那么此时 $f(i,j,k)=f(i,0,0)$.
• $f(0,0,0)=0$, $f(0,j,k)=INF$ 或 $-1$，因为不可以从 $f(0,j,k)$ 转移过来，算作不可达状态。因为我们如果保证恰好是凑出 $(j,k)$ 的话，那么只能从 $(0,0)$ 的状态转移过来。

#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
const int maxn = 25, maxm = 85;
int V1, V2, N, f[maxn][maxm];
int main() {
	memset(f, 0x3f, sizeof f);
	f[0][0] = 0;
	scanf("%d%d%d", &V1, &V2, &N);
	for (int i = 0; i < N; i++) {
		int v1, v2, w;
		scanf("%d%d%d", &v1, &v2, &w);
		for (int j = V1; j >= 0; j--) {
			for (int k = V2; k >= 0; k--) {
				f[j][k] = min(f[j][k], f[max(0, j - v1)][max(0, k - v2)] + w);
			}
		}
	}
	printf("%d\n", f[V1][V2]);
	return 0;
}

• 混合背包就是物品有的只能选 $1$ 件，有的可以选 $s$ 件，有的可以选无穷多件。
• 只有第二重循环不一样。所以边读入数据边求就可以。
• 注意到 $01$ 背包问题就是多重背包问题的特殊情况，可以统一处理。

#include<cstdio>
#include<algorithm>
using namespace std;
const int maxv = 1010;
int f[maxv], N, V;
int main() {
	scanf("%d%d", &N, &V);
	for (int i = 1; i <= N; i++) {
		int v, w, s;
		scanf("%d%d%d", &v, &w, &s);
		if (s == 0) {
			for (int j = v; j <= V; j++) f[j] = max(f[j], f[j - v] + w);
		}
		else {
			if (s == -1) s = 1;
			for (int k = 1; k <= s; s -= k, k *= 2) {
				for (int j = V; j >= v * k; j--) f[j] = max(f[j], f[j - k * v] + k * w);
			}
			if (s > 0) {
				for (int j = V; j >= v * s; j--) f[j] = max(f[j], f[j - s * v] + s * w);
			}
		}
	}
	printf("%d\n", f[V]);
	return 0;
}

• 题意：有 $N$ 个物品和一个容量是 $V$ 的背包。物品之间具有依赖关系，且依赖关系组成一棵树的形状。如果选择一个物品，则必须选择它的父节点。求背包物品最大价值。
• $f(u,j)$：从 $u$ 为根的子树中选，且总体积不超过 $j$ 时的价值最大值。
• 复杂度：$O(n^3)$
• 补充思路：对于结点 $u$，$son$ 是 $u$ 的一个子结点，$f(son,k),k\in [0,m-v[u]]$ 作为一组物品，分组背包.

#include<bits/stdc++.h>
using namespace std;
const int N = 110, V = 110;

int f[N][V], v[N], w[N];
int h[N], e[N], ne[N], idx;
int n, m;

void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

void dfs(int u)
{
    for(int i = h[u]; i != -1; i = ne[i])
    {
        int son = e[i];
        dfs(son);
        //分组背包，第一层循环背包体积，第二层循环每组的物品，即子树占用的体积。
        for(int j = m - v[u]; j >= 0; j--)
        {
            for(int k = j; k >= 0; k--)
            {
                f[u][j] = max(f[u][j], f[u][j - k] + f[son][k]);
            }
        }
    }
    //把根节点放进去
    //注意，这里不能取max，因为这个模拟的是选子节点必须选父结点的过程。
	//如果取max的话就意味着有些方案取子结点但没取父结点，结果可能会偏大。
    for(int j = m; j >= v[u]; j--)
    {
        f[u][j] = f[u][j - v[u]] + w[u];
    }
    //放不进根节点的方案，全部置为0.
    for(int j = 0; j < v[u]; j++) f[u][j] = 0;
}

int main()
{
    scanf("%d%d", &n, &m);
    memset(h, -1, sizeof h);
    int root;
    for(int i = 1; i <= n; i++)
    {
        int p;
        scanf("%d%d%d", &v[i], &w[i], &p);
        if(p == -1) root = i;
        else add(p, i);
    }
    dfs(root);
    printf("%d\n", f[root][m]);
}

优化至 $O(n^2)$

//林靖轩的写法
int dfs(int u)
{
    f[u][v[u]] = w[u], f[u][0] = 0;
    sz[u] = v[u];
    for(int i = h[u]; i != -1; i = ne[i])
    {
        int son = e[i];
        sz[u] += dfs(son);
        //分组背包，第一层循环背包体积，第二层循环每组的物品，即子树占用的体积。
        for(int j = min(sz[u], m); j >= v[u]; j--)
        {
            for(int k = j - v[u]; k >= 0; k--)
            {
                f[u][j] = max(f[u][j], f[u][j - k] + f[son][k]);
            }
        }
    }
    //放不进根节点的方案，全部置为0.
    for(int j = 0; j < v[u]; j++) f[u][j] = 0;
    return sz[u];
}

• 给定N个正整数$A_1,A_2,\dots ,A_N$，从中选出若干个数，使它们的和为 $M$，求有多少种选择方案.
• 都是这个套路，f(0, 0) 初始化为1.
• $f(0,0)=1,f(i,j)=f(i-1,j)+f(i,j-A_i)$.
• 方案数一定小心会不会爆 $int$ .

#include<cstdio>
#include<algorithm>
using namespace std;
const int maxm = 10010;
int N, M, f[maxm];
int main() {
	scanf("%d%d", &N, &M);
	f[0] = 1;
	for (int i = 0; i < N; i++) {
		int a;
		scanf("%d", &a);
		for (int j = M; j >= a; j--) {
			f[j] += f[j - a];
		}
	}
	printf("%d\n", f[M]);
	return 0;
}

• 题意：有 $N$ 件物品和一个容量是 $V$ 的背包。每件物品只能使用一次。第 $i$ 件物品的体积是 $v_i$，价值是 $w_i$。求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。输出 最优选法的方案数。注意答案可能很大，请输出答案模 $10^9+7$ 的结果。
• 注意这个题和上个题的区别，一个是恰好凑成 $m$，一个是凑成不超过 $m$.
• $f(i,j)$：前 $i$ 个物品，凑出体积恰好为 $j$ 的方案数（若定义成不超过 $j$，大雪菜说不好写，还要用到容斥原理）。
• 如果把此 $dp$ 问题看作一个 $DAG$ 上的最长路径统计问题，那么图的终点一定在最后一排即 $f[n,j]$. 因此方案数要把最后一排全部统计上。

二维：

#include<bits/stdc++.h>
using namespace std;
const int N = 1010, mod = 1e9 + 7;

int f[N][N], v[N], w[N], cnt[N][N];
int n, m;
int main()
{
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= n; i++)
    {
        scanf("%d%d", &v[i], &w[i]);
    }
    for(int i = 0; i <= n; i++) cnt[i][0] = 1;
    for(int i = 1; i <= n; i++)
    {
        for(int j = 0; j <= m; j++)
        {
            f[i][j] = f[i - 1][j], cnt[i][j] = cnt[i - 1][j];
            if(j >= v[i])
            {
                if(f[i][j] == f[i - 1][j - v[i]] + w[i])
                {
                    cnt[i][j] = (cnt[i][j] + cnt[i - 1][j - v[i]]) % mod;
                }
                else if(f[i][j] < f[i - 1][j - v[i]] + w[i])
                {
                    cnt[i][j] = cnt[i - 1][j - v[i]];
                    f[i][j] = f[i - 1][j - v[i]] + w[i];
                }
            }
        }
    }
    int res = 0;
    for(int j = 0; j <= m; j++)
    {
        if(f[n][j] == f[n][m]) res = (res + cnt[n][j]) % mod;
    }
    printf("%d\n", res);
}

压到1维滚动数组：

#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
const int maxn = 1010, mod = 1000000007;
int N, V, f[maxn], g[maxn];
int main() {
	scanf("%d%d", &N, &V);
	memset(f, -0x3f, sizeof f);
	f[0] = 0, g[0] = 1;
	for (int i = 1; i <= N; i++) {
		int v, w;
		scanf("%d%d", &v, &w);
		for (int j = V; j >= v; j--) {
			int maxv = max(f[j], f[j - v] + w);
			int cnt = 0;
            //在决策是否选择第i个物品时，需要看maxv是从哪个值过去的。
			if (maxv == f[j]) cnt += g[j];
			if (maxv == f[j - v] + w) cnt += g[j - v];
			cnt %= mod;
			g[j] = cnt, f[j] = maxv;
		}
	}
	int res = 0, ans = 0;
	for (int i = 0; i <= V; i++) res = max(res, f[i]);
	for (int i = 0; i <= V; i++) {
		if (f[i] == res) ans = (ans + g[i]) % mod;
	}
	printf("%d\n", ans);
	return 0;
}

• 小明手里有n元钱全部用来买书，书的价格为10元，20元，50元，100元。问小明有多少种买书方案？（每种书可购买多本）
• $f(0,0)=0.f(i,j)=f(i-1,j)+f(i-1,j-a_i)$.

#include<cstdio>
#include<algorithm>
using namespace std;
const int maxm = 1010;
int N, f[maxm], a[] = { 10, 20, 50, 100 };
int main() {
	scanf("%d", &N);
	f[0] = 1;
	for (int i = 0; i < 4; i++) {
		for (int j = a[i]; j <= N; j++) {
			f[j] += f[j - a[i]];
		}
	}
	printf("%d\n", f[N]);
	return 0;
}

• 题意：一个正整数n可以表示成若干个正整数之和，形如：$n=n_1+n_2+\dots +n_k$，其中$n_1\ge n_2\ge \dots \ge n_k,k\ge 1$。我们将这样的一种表示称为正整数 $n$ 的一种划分。现在给定一个正整数n，请你求出 $n$ 共有多少种不同的划分方法。
• 这个题类似一个完全背包问题，物品的体积分别是 $1\sim n$，每个物品选的次数无限制，问选出的物品体积恰好为n的选法有多少种。

有一个易错点。因为这次是有负数的，所以要吧 $f$ 初始化为 $-INF$，这个和代码设计有关。
感觉数字三角形还是从下往上走比较简单。

void solve() {
	for (int i = 0; i <= N; i++) {
		for (int j = 0; j <= i + 1; j++) {
			f[i][j] = -INF;
		}
	}
	f[1][1] = a[1][1];
	for (int i = 2; i <= N; i++) {
		for (int j = 1; j <= i; j++) {
			f[i][j] = max(f[i - 1][j - 1] + a[i][j], f[i - 1][j] + a[i][j]);
		}
	}
	int ans = -INF;
	for (int j = 1; j <= N; j++) ans = max(ans, f[N][j]);
	printf("%d\n", ans);
}

• 题意：设有 $N\times N$ 的方格图，我们在其中的某些方格中填入正整数，而其它的方格中则放入数字 0. 某人从图中的左上角 A 出发，可以向下行走，也可以向右行走，直到到达右下角的 B 点。在走过的路上，他可以取走方格中的数（取走后的方格中将变为数字 0）。此人从 A 点到 B 点共走了两次，试找出两条这样的路径，使得取得的数字和为最大。
• 这道题是不可以走两次，把路径记录下来的。因为两次都选择最优解的话，总体不一定是最优解。比如第一次可以不选择最优解，拿走一部分数字，第二次可以把剩下所有数字都拿走。但是，第一次选择最优解的话，可能第二次走的时候剩下的数字并不能拿走完。
• 这个题设 $f(k,i_1,i_2)$ 表示两条路径数字之和，两次位于点的位置分别为 $(i_1,j_1),(i_2,j_2)$，$k=i_1+i_2=j_1+j_2$，第一层先枚举 $k$，其实就是枚举走了多少步。然后一圈一圈向外扩展，因此每个格子只会走一次，不会重复。
• 两次走到同一点，等价于 $i_1+j_1=i_2+j_2$，且 $i_1=i_2$

#include<bits/stdc++.h>
using namespace std;
const int maxn = 15;
int N, f[maxn * 2][maxn][maxn], w[maxn][maxn];
int main() {
	scanf("%d", &N);
	int x, y, c;
	while (scanf("%d%d%d", &x, &y, &c) && x) {
		w[x][y] = c;
	}
	for (int k = 2; k <= 2 * N; k++) {
		for (int i1 = 1; i1 <= N; i1++) {
			for (int i2 = 1; i2 <= N; i2++) {
				int j1 = k - i1, j2 = k - i2;
				if (j1 < 1 || j1 > N || j2 < 1 || j2 > N) continue;
				int& x = f[k][i1][i2];
				int t = w[i1][j1];
				if (i1 != i2) t += w[i2][j2];
				x = max(x, f[k - 1][i1 - 1][i2 - 1] + t);
				x = max(x, f[k - 1][i1 - 1][i2] + t);
				x = max(x, f[k - 1][i1][i2 - 1] + t);
				x = max(x, f[k - 1][i1][i2] + t);
			}
		}
	}
	printf("%d\n", f[2 * N][N][N]);
	return 0;
}

• 题意：找到从 $(1,1)$ 到 $(m,n)$ 的两条路径，两条路径除了起点和终点外没有相交的点，且两条路径的点权之和最大。
• 这个题呀，和方格取数的做法一模一样。
• 证明：

1. 第二次传纸条改个方向，和从左上到右下传是等效的。
2. 任何两条路径，都可以改为一条路径在另一条路径的上方。比如这个，交换颜色就行。
   
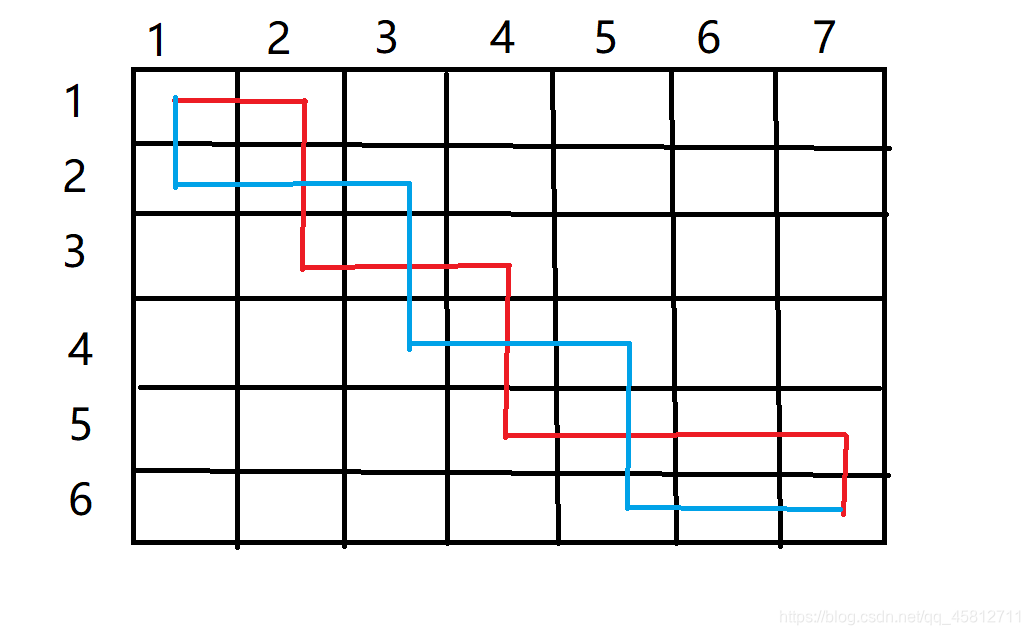
3. 第三点，把实线换成虚线，结果不会变差。因为重合的点，第二次经过的时候是 0，但是绕个圈之后，对称点不一定是 0.
   

• 因此，这道题只需要改一下读入，以及注意N和M，其他的都一样。
• 当然，这道题完全可以加一句判断，除了起点和终点，只有 $i_1\ne i_2$ 时才更新状态，这样也是对的
• 因此，不管是在方格取数中，还是在本问题中，走的两条路径，除了起点和终点外，一定没有交点。

动态规划嘛，看看需要几维才能把状态表示出来。先考虑1维。一维不够再上升。其实几维不代表循环就有几重。
朴素版：

void solve() {
	for (int i = 1; i <= N; i++) {
		f[i] = 1;
		for (int j = 1; j <= i; j++) {
			if (a[j] < a[i]) f[i] = max(f[i], f[j] + 1);
		}
	}
	int ans = 0;
	//千万小心，答案是取max，不是f[N].
	for (int i = 1; i <= N; i++) ans = max(ans, f[i]);
	printf("%d\n", ans);
}

寻找公共子序列（倒着输出）：

void solve() {
	for (int i = 1; i <= N; i++) {
		f[i] = 1, g[i] = 0;
		for (int j = 1; j <= i; j++) {
			if (a[j] < a[i]) {
				if (f[i] < f[j] + 1) {
					g[i] = j;
					f[i] = f[j] + 1;
				}
			}
		}
	}
	int k = 0;
	for (int i = 1; i <= N; i++) {
		if (f[i] > f[k]) k = i;
	}
	printf("%d\n", f[k]);
	for (int i = 0, len = f[k]; i < len; i++) {
		printf("%d ", a[k]);
		k = g[k];
	}
}

优化版：

void solve() {
	fill(f, f + N, INF);
	for (int i = 1; i <= N; i++) {
		*lower_bound(f, f + N, a[i]) = a[i];
	}
	printf("%d\n", lower_bound(f, f + N, INF) - f);
}

• 题意：找一个上升子序列，是它的和是最大的。

for (int i = 1; i <= N; i++) {
	f[i] = a[i];
	for (int j = 1; j <= i; j++) {
		if (a[j] < a[i]) f[i] = max(f[i], f[j] + a[i]);
	}
}
int ans = 0;
for (int i = 1; i <= N; i++) ans = max(ans, f[i]);

• 题意：定义大于等于的偏序关系，问这样的偏序关系最少可以分为几条链。

• 题意：一套防御系统的导弹拦截高度要么一直 严格单调 上升要么一直 严格单调 下降。给定即将袭来的一系列导弹的高度，请你求出至少需要多少套防御系统，就可以将它们全部击落。

• 这个题很妙的地方是，巧用贪心，up数组一定是单调递减的，如果一个数字可以放进来，一定要放到尽可能考前的组里面去。

• 求 $A$ 和 $B$ 的最长公共上升子序列，$n\le 3000.$

• 设 $f(i,j)$ 为 $a$ 的前 $i$ 项，$b$ 的前 $j$ 项，且以 $b[j]$ 结尾的最长公共上升子序列. 难点在于当 $a[i]=b[j]$ 时迅速找到所有满足 $b[k]<b[j]$ 的 f(i. k) 的最大值. 但是我们注意到 $a[i]=b[j]$，因此只需找到 $b[k]<a[i]$ 且 $f(i,k)$ 最大值即可。这个可以在每一层 $i$ 固定的循环中记录下来，$f(i,j)$ 可以从这个地方转移过来.

• 当 $f(i,j)$ 不包含 $a[i]$ 时，$f(i,j)=f(i-1,j)$；当包含 $a[i]$ 时， f ( i , j ) = m a x { f ( i , 1 ) , f ( i , 2 ) . . . f ( i , j − 1 ) } + 1 f(i, j) = max\{f(i, 1), f(i, 2) ... f(i,j-1)\}+1 f(i,j)=max{f(i,1),f(i,2)...f(i,j−1)}+1.

• 两个序列的问题，一般可以开二维数组，$f(i,j)$ 是第一个序列前 $i$ 项，第二个序列前 $j$ 项组成的两个序列对应的答案。这里的是目前所求出的公共子序列在第一个序列前 $i$ 个数中出现，在第二个序列前 $j$ 个数中出现。
  这个涉及到字符串的题目一定要小心，因为下标是从1开始读的，因此读入的时候要读到 $s+1$ 的位置。
• $s_1...s_i$ 和 $t_1...t_j$ 的公共子列可能是：

1. $s_1...s_{i-1}$ 和 $t_1...t_{j-1}$ 的公共子列末尾追加 $s_i$，当且仅当 $s_i=t_j$.
2. $s_1...s_{i-1}$ 和 $t_1...t_j$ 的公共子列
3. $s_1...s_i$ 和 $t_1...t_{j-1}$ 的公共子列。

#include<cstdio>
#include<algorithm>
using namespace std;
const int maxn = 1010;
int f[maxn][maxn], N, M;
char s1[maxn], s2[maxn];
void solve() {
	for (int i = 1; i <= N; i++) {
		for (int j = 1; j <= M; j++) {
			if (s1[i] == s2[j]) f[i][j] = f[i - 1][j - 1] + 1;
			else f[i][j] = max(f[i - 1][j], f[i][j - 1]);
		}
	}
	printf("%d\n", f[N][M]);
}
int main() {
	scanf("%d%d%s%s", &N, &M, s1 + 1, s2 + 1);
	solve();
	return 0;
}

题意：给定两个字符串 $A$ 和 $B$，现在要将 $A$ 经过若干操作变为 $B$，可进行的操作有：

1. 删除–将字符串 $A$ 中的某个字符删除。
2. 插入–在字符串 $A$ 的某个位置插入某个字符。
3. 替换–将字符串 $A$ 中的某个字符替换为另一个字符。

现在请你求出，将 $A$ 变为 $B$ 至少需要进行多少次操作。

• 设 $f(i,j)$ 为把 $A$ 的前 $i$ 个字符变成 $B$ 的前 $j$ 个字符需要的最少操作步骤.
  • 若 $a[i]=b[j]$，则 $f(i,j)=f(i-1,j-1)$.
  • 若 $a[i]\ne b[j]$
    • 可以先删掉 $a[i]$，然后从 $a[1:i-1]$ 变成 $b[i:j]$，即 $f(i-1,j)+1$.
    • 先从 $a[1:i]$ 变成 $b[1:j-1]$，然后在结尾加上 $b[j]$，即 $f(i,j-1)+1$.
    • 可以把 $a[1:i-1]$ 变为 $b[1:j-1]$，然后把 $a[i]$ 变为 $b[j]$，即 $f(i-1,j-1)+1$.
• 一定要注意动态规划遇到字符串时，读取到 $s+1$ 的位置。

void solve() {
	for (int i = 0; i <= N; i++) f[i][0] = i;
	for (int j = 0; j <= M; j++) f[0][j] = j;
	for (int i = 1; i <= N; i++) {
		for (int j = 1; j <= M; j++) {
		 //第一个是删（本来i-1和j匹配，删掉第i位使其继续匹配），第二个是增（本来是i和j-1匹配，在增加一个和第j位匹配）。
			f[i][j] = min(f[i - 1][j] + 1, f[i][j - 1] + 1);  
			if (a[i] == b[j]) f[i][j] = min(f[i][j], f[i - 1][j - 1]);  //相等，直接到下一位
			else f[i][j] = min(f[i][j], f[i - 1][j - 1] + 1);   //替换
		}
	}
	printf("%d\n", f[N][M]);
}

• 拓扑排序 + 记忆化搜索
• 这里的 $f(x,y)$ 的意思是，从 $(x,y)$ 这个点出发，能够下滑的最大距离是多少。这样的话，每次发现一个比 $(x,y)$ 高的一个点，就可以将这个点对应的 f 值更新为 $max(f,f(x,y)+1)$.

#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
const int maxn = 310;
int N, M, f[maxn][maxn], h[maxn][maxn];
int dx[] = { 1, -1, 0, 0 }, dy[] = { 0, 0, 1, -1 };
int dp(int x, int y) {
	int& v = f[x][y];
	if (v != -1) return v;
	v = 1;
	for (int i = 0; i < 4; i++) {
		int nx = x + dx[i], ny = y + dy[i];
		if (1 <= nx && nx <= N && 1 <= ny && ny <= M && h[nx][ny] < h[x][y]) {
			v = max(v, dp(nx, ny) + 1);
		}
	}
	return v;
}
int main() {
	scanf("%d%d", &N, &M);
	for (int i = 1; i <= N; i++) {
		for (int j = 1; j <= M; j++) {
			scanf("%d", &h[i][j]);
		}
	}
	memset(f, -1, sizeof f);
	int res = 0;
	for (int i = 1; i <= N; i++) {
		for (int j = 1; j <= M; j++) {
			res = max(res, dp(i, j));
		}
	}
	printf("%d\n", res);
	return 0;
}

• 题意：街上一共有 $N$ 家店铺，不能抢劫相邻两家的店铺，问收益最大值。
• $f(i,j)$：走到了第 $i$ 步，且状态为 j 时，收益最大值。$j=0$ 表示没有抢第 $i$ 家店，$j=1$ 表示抢了第 $i$ 家店。
• f ( i , 0 ) = m a x { f ( i − 1 , 0 ) , f ( i − 1 , 1 ) } f(i, 0) = max\{f(i-1, 0),f(i-1,1)\} f(i,0)=max{f(i−1,0),f(i−1,1)}
• $f(i,1)=f(i-1,0)+w[i]$.

#include<cstdio>
#include<algorithm>
using namespace std;
const int maxn = 100010, INF = 0x3f3f3f3f;
int f[maxn][2], w[maxn], N;
int main() {
	int T;
	scanf("%d", &T);
	f[0][0] = 0, f[0][1] = -INF;
	while (T--) {
		scanf("%d", &N);
		for (int i = 1; i <= N; i++) scanf("%d", &w[i]);
		for (int i = 1; i <= N; i++) {
			f[i][0] = max(f[i - 1][0], f[i - 1][1]);
			f[i][1] = f[i - 1][0] + w[i];
		}
		printf("%d\n", max(f[N][0], f[N][1]));
	}
	return 0;
}