💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码及文献

---

💥1 概述

文献来源：

 本文研究了变分贝叶斯方法在线性状态空间模型中动态状态和时变测量噪声参数联合递归估计中的应用。所提出的自适应卡尔曼滤波方法基于对各时间步上状态和噪声参数的联合后验分布分别形成可分离变分近似。结果是一个递归算法，其中每一步都用卡尔曼滤波器估计状态，并通过定点迭代估计噪声方差的足够统计数据。通过仿真数据演示了该算法的性能。

原文摘要：

Abstract:

This article considers the application of variational Bayesian methods to joint recursive estimation of the dynamic state and the time-varying measurement noise parameters in linear state space models. The proposed adaptive Kalman filtering method is based on forming a separable variational approximation to the joint posterior distribution of states and noise parameters on each time step separately. The result is a recursive algorithm, where on each step the state is estimated with Kalman filter and the sufficient statistics of the noise variances are estimated with a fixed-point iteration. The performance of the algorithm is demonstrated with simulated data.

卡尔曼滤波器 （KF） [1] 考虑了估计问题类中噪声测量的动态状态估计，其中动态和测量过程可以通过线性高斯状态空间模型近似。扩展卡尔曼滤波器（EKF）和无迹卡尔曼滤波器（UKF）通过形成后验状态分布的高斯近似[2]–[5]，将该方法扩展到非线性动态和测量模型。这些滤波器的一个严重限制是，它们假定完全了解测量和动态模型参数，包括噪声统计。参数的确切知识，特别是噪声统计，在许多实际情况中并不是一个合理的假设。这种应用的例子是低成本的集成GPS/INS定位系统和容错系统（例如，见[6]、[7]及其中的参考资料）。

解决不确定参数问题的经典方法（参见[8]，[9]）是使用自适应滤波器，其中模型参数或噪声统计与动态状态一起估计。经典的噪声自适应滤波方法可分为贝叶斯、最大似然、相关和协方差匹配方法[8]。贝叶斯方法是其中最通用的，其他方法通常可以解释为贝叶斯方法的近似值。贝叶斯噪声自适应滤波方法的例子是基于状态增强的方法[10]，[11]，多模型方法，如交互多模型（IMM）算法[3]，[9]和粒子方法[12]-[15]。

变分贝叶斯（VB）方法已被开发用于各种模型，与采样方法相比，以较低的计算成本执行近似后验推理（有关VB方法的回顾，请参阅例如[16]-[18]）。 这些方法假设后部采用更简单、易于分析的形式。两种主要方法是推导因式自由形式分布（对于共轭指数类中的模型），或者假设固定形式的后验分布（例如，多元高斯，可能具有模型的适当参数化）。

Smidl和Quinn[19]提出了VB近似的理论框架，特别强调了递归贝叶斯推理和信号处理应用。与本工作相关，还考虑了具有未知方差的AR模型的VB近似，但未考虑具有未知时变方差的一般线性状态空间模型。卡尔曼平滑器的通用变分版本在[20]中已经开发出来，利用共轭指数框架，但具有平稳噪声。时变方差模型已在 [21] 中使用固定形式方法解决。

我们提出的方法通过分解的自由形式分布来近似状态的联合后验分布和噪声方差。该近似在每个时间步上分别形成，结果是一个递归算法，其中在每个步骤上，状态和噪声方差的足够统计数据都是通过卡尔曼滤波器的定点迭代估计的。我们还提出了方差的启发式动力学模型，可用于对噪声的时间行为进行建模，同时仍保留近似后验分布的功能形式。

📚2 运行结果

部分代码：

for t = 2:Tn
        %%%%True noise covariance matrices
        Q = (1+0.5*cos(pi*t/Tn))*Q0;
        R = (1+0.6*cos(pi*t/Tn))*R0;
        %%%%Square-root of noise covariance matrices
        SQ = utchol(Q);
        SR = utchol(R);
        %%%%Simulate true state and measurement
        x = F*x+SQ*randn(nx,1);
        z = H*x+SR*randn(nz,1);
        X(:,t) = x;
        %%%%Filtering
        [x1,P_Const,Ppf] = kf(x1,P_Const,F,H,z,Q0,R0*times_Of_R);
        [x2,P_True,Pptf] = kf(x2,P_True,F,H,z,Q,R);
        [x3,P_VB,alfa,beta,mk] = vbkf(x3,P_VB,alfa,beta,mk,F,H,z,Q0,N);
        %%%%Save data
        XKF_Const(:,t) = x1;
        XKF_True(:,t) = x2;
        XKF_VB(:,t) = x3;
    end
    %%%%MSE calculation
    mse_Kf_1(:,k) = (X(1,:)-XKF_Const(1,:)).^2+(X(2,:)-XKF_Const(2,:)).^2;
    mse_Kf_2(:,k) = (X(3,:)-XKF_Const(3,:)).^2+(X(4,:)-XKF_Const(4,:)).^2;

    mse_Ktf_1(:,k) = (X(1,:)-XKF_True(1,:)).^2+(X(2,:)-XKF_True(2,:)).^2;
    mse_Ktf_2(:,k) = (X(3,:)-XKF_True(3,:)).^2+(X(4,:)-XKF_True(4,:)).^2;

    mse_VB_1(:,k) = (X(1,:)-XKF_VB(1,:)).^2+(X(2,:)-XKF_VB(2,:)).^2;
    mse_VB_2(:,k) = (X(3,:)-XKF_VB(3,:)).^2+(X(4,:)-XKF_VB(4,:)).^2;
end

%%%%%%%%%RMSE calculation
rmse_Kf_1 = sqrt(mean(mse_Kf_1,2));
rmse_Kf_2 = sqrt(mean(mse_Kf_2,2));
rmse_Ktf_1 = sqrt(mean(mse_Ktf_1,2));
rmse_Ktf_2 = sqrt(mean(mse_Ktf_2,2));

rmse_VB_1 = sqrt(mean(mse_VB_1,2));
rmse_VB_2 = sqrt(mean(mse_VB_2,2));
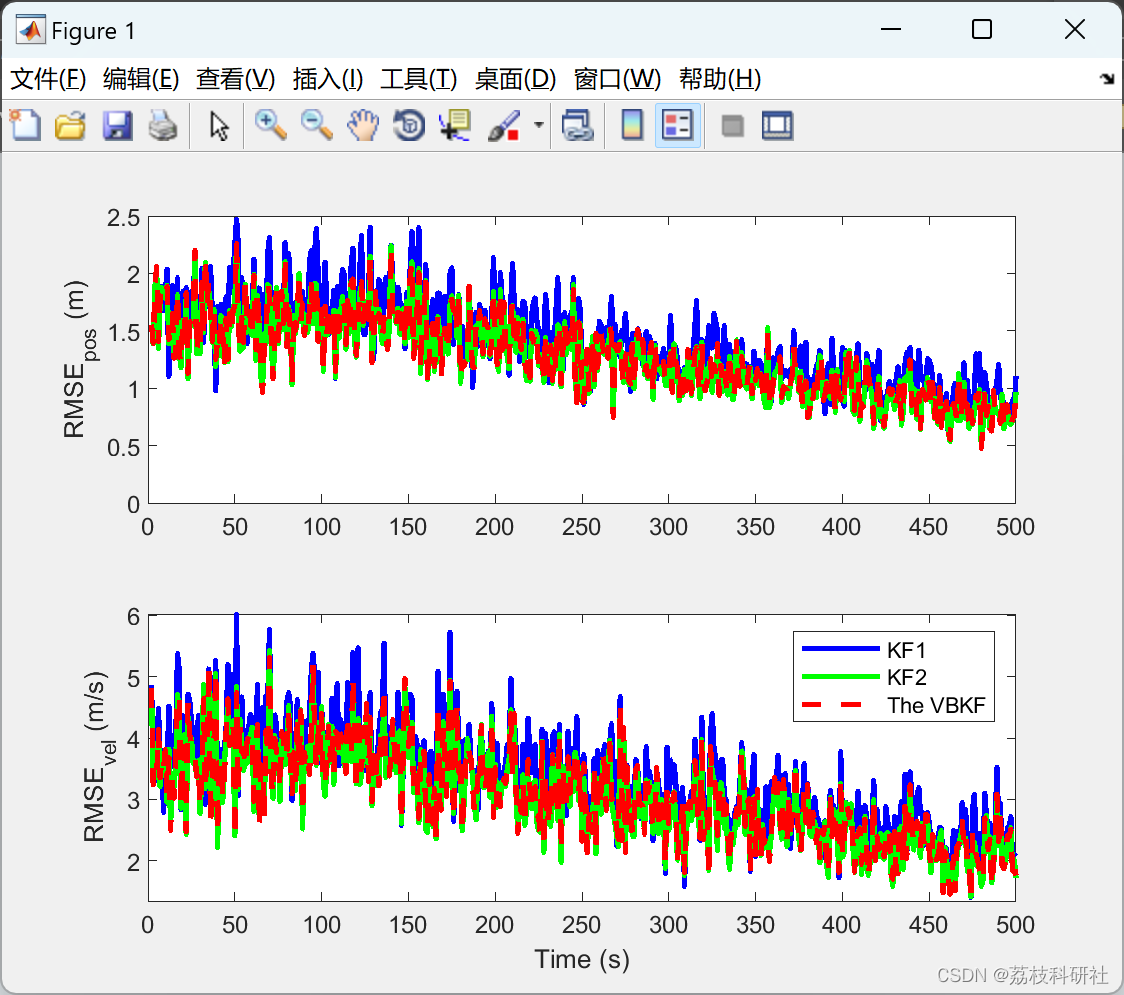
%%%%%%%RMSE curves
figure;
j = 2:L;
subplot(2,1,1)
plot(j*T,rmse_Kf_1(2:end),'-b',j*T,rmse_Ktf_1(2:end),'-g',j*T,rmse_VB_1(2:end),'--r','linewidth',2);
ylabel('RMSE_{pos} (m)');
subplot(2,1,2)
plot(j*T,rmse_Kf_2(2:end),'-b',j*T,rmse_Ktf_2(2:end),'-g',j*T,rmse_VB_2(2:end),'--r','linewidth',2);
xlabel('Time (s)');
ylabel('RMSE_{vel} (m/s)');
legend('KF1','KF2','The VBKF');

🎉3 参考文献

部分理论来源于网络，如有侵权请联系删除。

[1]S. Sarkka and A. Nummenmaa, "Recursive Noise Adaptive Kalman Filtering by Variational Bayesian Approximations," in IEEE Transactions on Automatic Control, vol. 54, no. 3, pp. 596-600, March 2009, doi: 10.1109/TAC.2008.2008348.

🌈4 Matlab代码及文献