Dijkstra算法求最短路

news2024/11/19 7:31:10

Dijkstra算法是单源最短路算法，是用来求一个点到其他所有点点最短距离，使用小根堆优化后时间复杂度大概为 $O m l o g n$

注意：不可以解决存在负权边的问题

【模板】单源最短路径（标准版）

链接：https://www.luogu.com.cn/problem/P4779

题目描述

给定一个 $n$ 个点， $m$ 条有向边的带非负权图，请你计算从 $s$ 出发，到每个点的距离。

数据保证你能从 $s$ 出发到任意点。

输入格式

第一行为三个正整数 $n, m, s$ 。
第二行起 $m$ 行，每行三个非负整数 $u_i, v_i, w_i$ ，表示从 $u_i$ 到 $v_i$ 有一条权值为 $w_i$ 的有向边。

输出格式

输出一行 $n$ 个空格分隔的非负整数，表示 $s$ 到每个点的距离。

样例 #1

样例输入 #1

样例输出 #1

0 2 4 3

提示

$\leq n \leq 10^5$ ；

$\leq m \leq 2\times 10^5$ ；

$s = 1$ ；

$\leq u_i, v_i\leq n$ ；

$\leq w_i \leq 10 ^ 9$ ,

$\leq \sum w_i \leq 10 ^ 9$ 。

思路-朴素

初始化时，dist[]数组全部初始化为无穷大，dist[1]=0
从圈中选择一个距离最小的点u,打上标记st[u]=1表示这个点出圈
对u的所有出边进行松弛操作【尝试更新相邻点的最小距离】
重复2，3步骤，直到圈内为空

代码- $O(n^2)$

下面代码是用邻接矩阵求1-n的最短路

#include <iostream>
#include<cstring>
using namespace std;

const int N = 510;

int g[N][N]; //为稠密阵所以用邻接矩阵存储
bool st[N];//用于记录该点的最短距离是否已经确定
int dist[N]; //用于记录每一个点距离第一个点的距离
int n, m;

int Dijkstra()
{
	memset(dist, 0x3f, sizeof dist);
	dist[1] = 0; //第一个点到自身的距离为0
	for (int i = 0; i < n; ++i)
	{
		int u = i; //当前访问的点
		for (int j = 1; j <= n; j++) if (!st[j] && dist[j] < dist[u]) u = j; //寻找距离最小的点
		st[u] = true;
		//依次更新每个点所到相邻的点路径值
		for (int j = 1; j <= n; j++) dist[j] = min(dist[j], dist[u] + g[u][j]);
	}
	if (dist[n] == 0x3f3f3f3f) return -1; //不存在
	return dist[n];
}

int main()
{
	cin >> n >> m;
	memset(g, 0x3f, sizeof g);
	while (m--)
	{
		int x, y, z;
		cin >> x >> y >> z;
		g[x][y] = min(g[x][y], z); //如果发生重边的情况则保留最短的一条边
	}
	cout << Dijkstra() << endl;
	return 0;
}

思路-堆优化

算法的主要耗时的步骤是从dist 数组中选出：没有确定最短路径的节点中距离源点最近的点 t。

只是找个最小值而已，没有必要每次遍历一遍dist数组。所以这里可以使用小根堆来维护。

代码- $O (m l o g n)$

#include <bits/stdc++.h>

#define int long long
using namespace std;

const int N = 1e5 + 10;
typedef pair<int, int> PII;
typedef struct edge {
    int y, w;
} edge;

vector<edge> e[N];
int dist[N];
bool st[N];
int n, m, s;

void Dijkstra() {
    priority_queue<PII, vector<PII>, greater<>> q;
    q.push({0, s});
    for (int i = 1; i <= n; i++) dist[i] = 1e18;
    dist[s] = 0;
    while (q.size()) {
        auto [d, x] = q.top();
        q.pop();
        if (st[x]) continue;
        st[x] = true;
        for (auto [y, w]: e[x]) {
            if (dist[y] > dist[x] + w) {
                dist[y] = dist[x] + w;
                q.push({dist[y], y});
            }
        }
    }
}

signed main() {
#ifndef ONLINE_JUDGE
    freopen("test.in", "r", stdin);
    freopen("test.out", "w", stdout);
#endif
    cin >> n >> m >> s;
    while (m--) {
        int a, b, c;
        cin >> a >> b >> c;
        e[a].push_back({b, c});
    }
    Dijkstra();
    for (int i = 1; i <= n; i++) {
        cout << dist[i] << " ";
    }


    return 0;
}

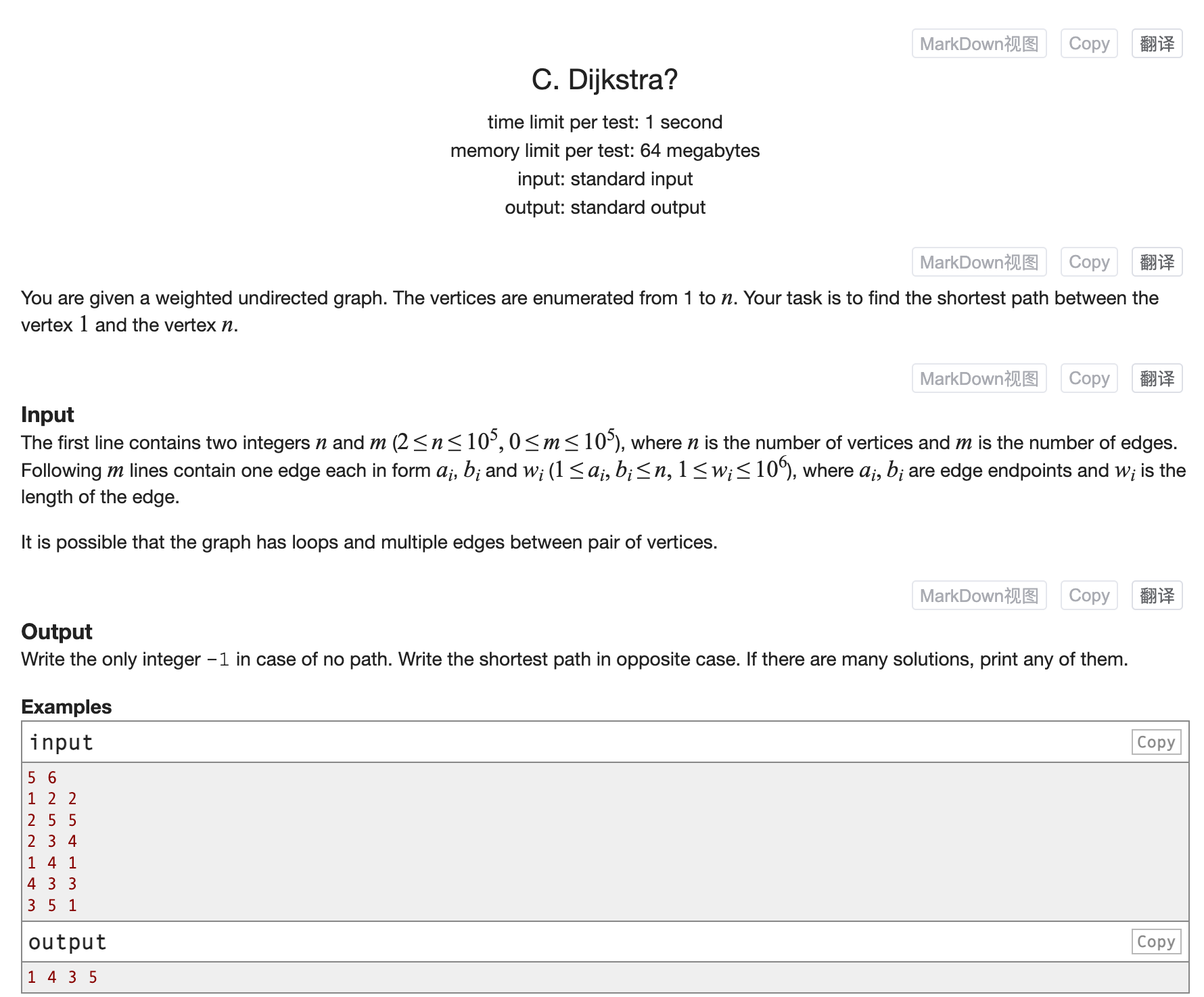
Codeforces Alpha Round 20 (Codeforces format)-C. Dijkstra?

题目

思路

Dijkstra算法的模版题目，这里需要求从1走到n到最短路径长度，

可以先跑一遍Dijkstra算法
然后从终点开始往前找是从哪个点转移过来的，即满足dist[x]=dist[y]+w,y为x的邻点，w为边权
最后需要把路径反转一下

代码

#include <bits/stdc++.h>
#define int long long
#define yes cout << "YES" << endl;
#define no cout << "NO" << endl;
using namespace std;

typedef pair<int, int> PII;
const int N = 1e5 + 10;
typedef struct edge {
    int to, w;
} edge;

vector<edge> e[N];
int dist[N];
bool st[N];
int n, m;

void dijkstra() {
    priority_queue<PII, vector<PII>, greater<>> q;
    q.push({0, 1});
    for(int i=1;i<=n;i++){
        dist[i]=1e18;
    }
    dist[1] = 0;
    while (q.size()) {
        auto [distance, x] = q.top();
        q.pop();
        if (st[x])
            continue;
        st[x] = true;
        for (auto [y, w] : e[x]) {
            if (dist[x] + w < dist[y]) {
                dist[y] = dist[x] + w;
                q.push({dist[y], y});
            }
        }
    }
}
void solve() {
    cin >> n >> m;
    while (m--) {
        int a, b, c;
        cin >> a >> b >> c;
        e[a].push_back({b, c});
        e[b].push_back({a, c});
    }
    dijkstra();

    if (dist[n] == 1e18) {
        cout << -1 << endl;
    } else {
        int t = dist[n];
        vector<int> path;
        path.push_back(n);
        int x = n;
        while (t != 0) {
            for (auto [y, w] : e[x]) {
                if (dist[x] == dist[y] + w) {
                    path.push_back(y);
                    x = y;
                    t-=w;
                    break;
                }
            }
        }
        reverse(path.begin(),path.end());

        for(auto x:path){
            cout<<x<<" ";
        }
    }
}
signed main() {
    int _ = 1;
    while (_--)
        solve();
    return 0;
}