1.题目链接:
51. N 皇后
2.解题思路:
2.1.题目要求:
给一个数字 n ,要求返回所有 n 个 皇后能在 n X n 的棋盘上 不相互攻击 的情况。
能攻击到的情况:以皇后自身为原点,横、竖、同斜线(45度、135度)都可以被攻击到。
下图为n=4的时候,4 个皇后在 4 X 4 棋盘的所有生存情况。
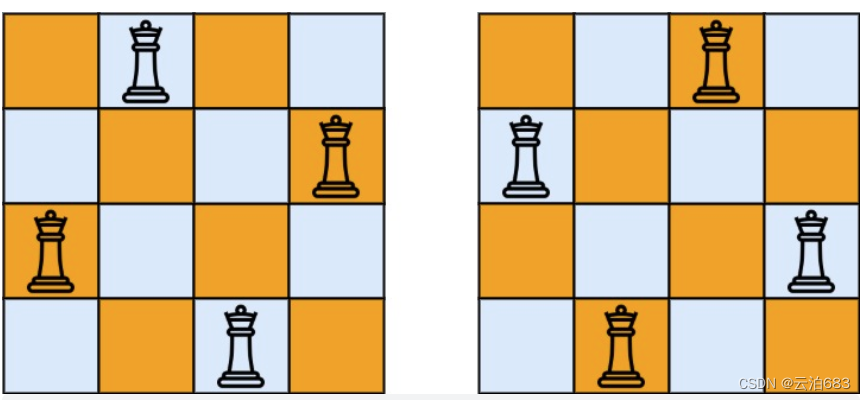
2.2.思路:
处理本体,要求对二维数组进行处理,for循环的 i 当作横轴 ,然后再自建一个纵轴row,就可以遍历整个棋盘了,每走一步就判断一次,该皇后位置对其他皇后位置的威胁,有威胁继续遍历,没有就把皇后落在这里,终止条件就是到叶子节点
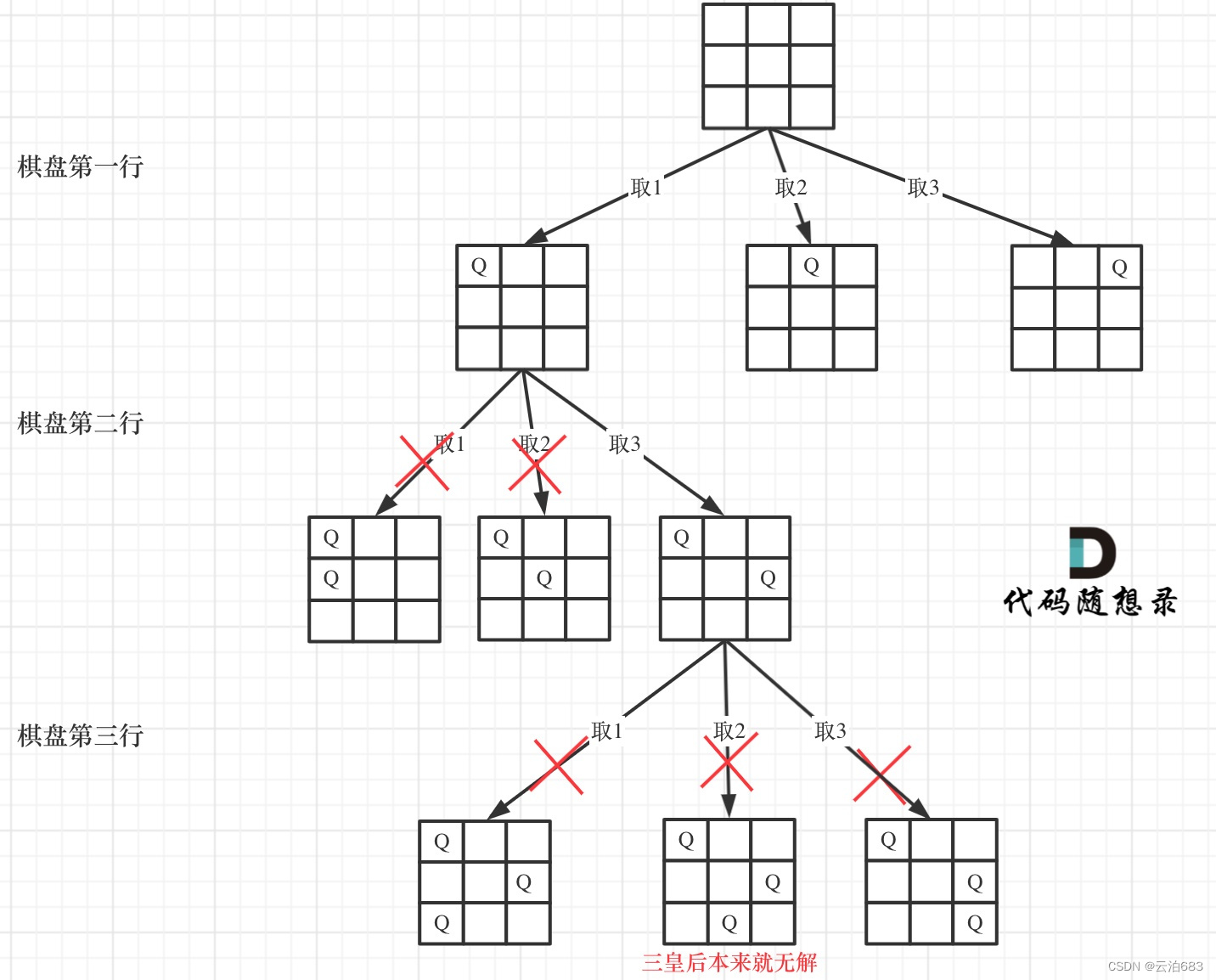
2.3.回溯三部曲:
col == column == 纵行 y
2.3.1.确定回溯函数参数
需要一个 row + for循环的col( i ) 来遍历棋盘
vector<vector<string>> result;
void backtracking(int n, int row, vector<string>& chessboard) {2.3.2.确定终止条件
if (row == n) {
result.push_back(chessboard);
return;
}
2.3.3.确定单层遍历逻辑
判断皇后Q再在这位置合不合适,合适落点继续遍历,不合适继续找合适的
for (int col = 0; col < n; col++) {
if (isValid(row, col, chessboard, n)) { // 验证合法就可以放
chessboard[row][col] = 'Q'; // 放置皇后
backtracking(n, row + 1, chessboard);
chessboard[row][col] = '.'; // 回溯,撤销皇后
}
}
2.3.4.如何判断皇后在当前位置和其他皇后会不会冲突?
按照如下标准判断:
- 不能同行
- 不能同列
- 不能同斜线 (45度和135度角)
行没有判断是因为for循环,一行只放一个皇后的,直接满足了皇后不能在同一行的规则。
代码如下:
bool isValid(int row, int col, vector<string>& chessboard, int n) {
// 检查列
for (int i = 0; i < row; i++) { // 这是一个剪枝
if (chessboard[i][col] == 'Q') {
return false;
}
}
// 检查 45度角是否有皇后
for (int i = row - 1, j = col - 1; i >=0 && j >= 0; i--, j--) {
if (chessboard[i][j] == 'Q') {
return false;
}
}
// 检查 135度角是否有皇后
for(int i = row - 1, j = col + 1; i >= 0 && j < n; i--, j++) {
if (chessboard[i][j] == 'Q') {
return false;
}
}
return true;
}
2.4.总代码:
class Solution {
private:
vector<vector<string>> result;
// n 为输入的棋盘大小
// row 是当前递归到棋盘的第几行了
void backtracking(int n, int row, vector<string>& chessboard) {
if (row == n) {
result.push_back(chessboard);
return;
}
for (int col = 0; col < n; col++) {
if (isValid(row, col, chessboard, n)) { // 验证合法就可以放
chessboard[row][col] = 'Q'; // 放置皇后
backtracking(n, row + 1, chessboard);
chessboard[row][col] = '.'; // 回溯,撤销皇后
}
}
}
bool isValid(int row, int col, vector<string>& chessboard, int n) {
// 检查列
for (int i = 0; i < row; i++) { // 这是一个剪枝
if (chessboard[i][col] == 'Q') {
return false;
}
}
// 检查 45度角是否有皇后
for (int i = row - 1, j = col - 1; i >=0 && j >= 0; i--, j--) {
if (chessboard[i][j] == 'Q') {
return false;
}
}
// 检查 135度角是否有皇后
for(int i = row - 1, j = col + 1; i >= 0 && j < n; i--, j++) {
if (chessboard[i][j] == 'Q') {
return false;
}
}
return true;
}
public:
vector<vector<string>> solveNQueens(int n) {
result.clear();
std::vector<std::string> chessboard(n, std::string(n, '.'));
backtracking(n, 0, chessboard);
return result;
}
};
3.遇见的问题:
怎么 row == n 就返回了呢?
(按我的理解,这个时候还没遍历完Q(皇后)在row == n 这一行的可能性,直接返回,那不完整啊)
哦哦,他进入第一次递归状态的时候才 row 才+1,如下图,当搜索最后一层的 row == 2 的时候 ,因为 row == 3 才停止搜索,所以还会继续向下递归,继续递归 row +1 ,触发终止条件,返回。
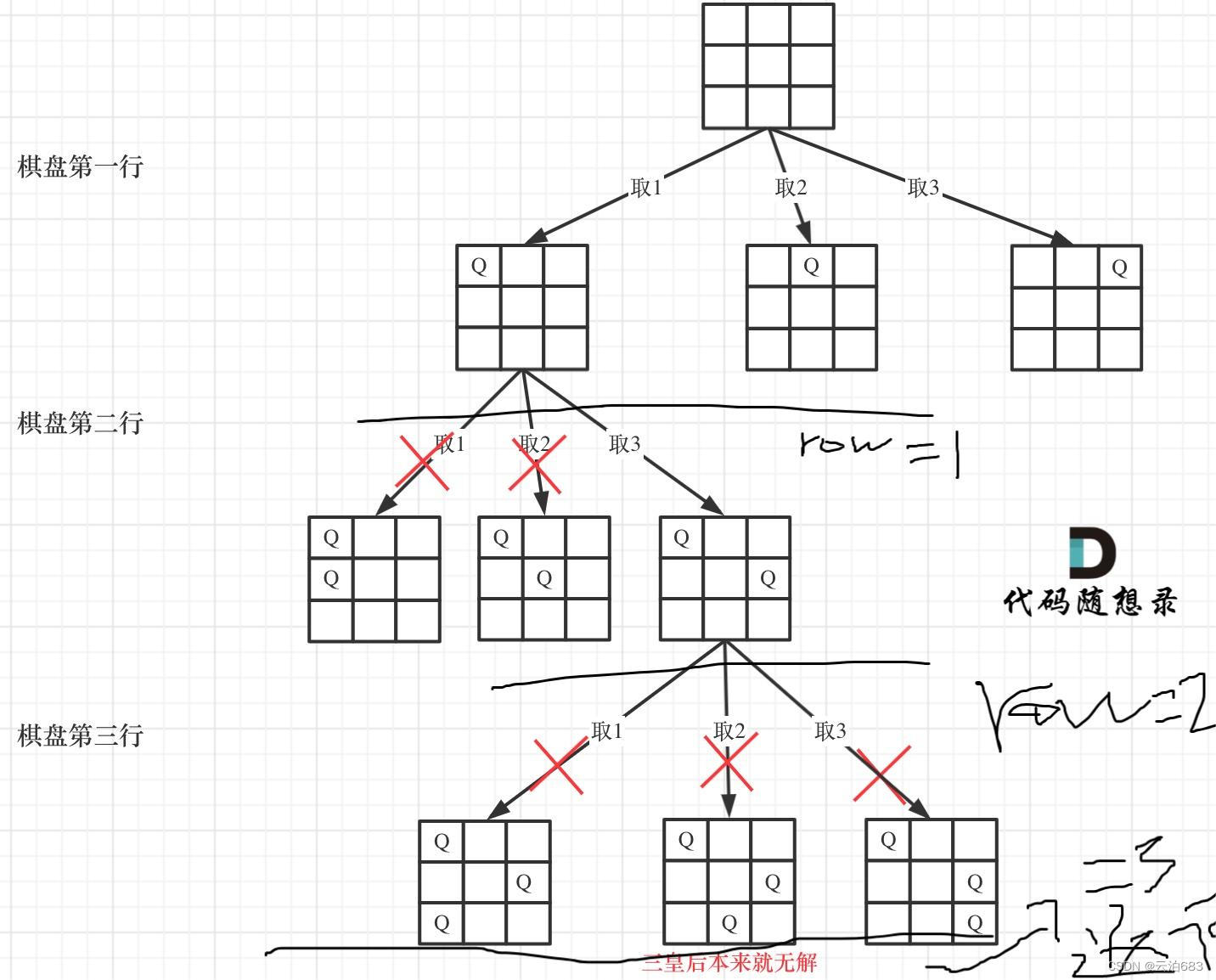
没有返回方案失败的情况吗?
(n = 3,放置会失败,代码里感觉好像没有对应的情况)
题目要求返回方案...那返回的方案不完整也就是意思是无解的意思吧..这样理解好了。
确认皇后45度和135度的代码怎么理解?
(感觉判断皇后在当前位置合不合适的代码看不懂啊,45度和135度哪里,可能现在脑子有点不好使,下次来看)
哦哦,代码只往皇后的135度和45度上查,因为只有上面才有皇后,下面还没去放皇后,因为上面还没放好。
(先入为主了,还是把条件列清楚,画个图合适)
C++中的std::是什么?
std:: 是个名称空间标示符,C++标准库中的函数或者对象都是在命名空间std中定义的,所以我们要使用标准函数库中的函数或对象都要使用std来限定。
(命名的时候删掉都可以通过,所以干嘛加这玩意...)
4.记录:
不用太贪,处理完N皇后先,感觉前面那道飞机也可以处理,题目理解了,不过要去学map和set。





![[附源码]JAVA毕业设计农产品的物流信息服务平台(系统+LW)](https://img-blog.csdnimg.cn/e55ce54cd8554e9d92ccdb59127adb37.png)

![[附源码]计算机毕业设计社区生活废品回收APPSpringboot程序](https://img-blog.csdnimg.cn/9d32129672704204aa07472b1e1baa94.png)