目录

1.惯性系

2.非惯性系

3.惯性力 

题1

题目描述

题解

4.动量定理

题2

题目描述

题解

5.动量守恒定律

题3

题目描述

题解

---

1.惯性系

牛顿定律适用的参考系，总能在找到特殊的参照物群（参考系），使得牛顿第一定律成立，那么这个参考系成为惯性系。

2.非惯性系

牛顿定律不适用的参考系。

“受力” “自转” “加速”——非惯性系

下图就是就是一个典型的需要用到非惯性参考系的场景。

3.惯性力 

在非惯性系中，牛顿运动定律是不适用的。但是，也可以假象在非惯性系中，除了相互作用所引起的力以外，还受到一种由于非惯性系而引起的力——惯性力

上图小车内部的小球就受到一个不存在的力——惯性力，才能拥有速度v'和加速度a'。

题1

题目描述

一升降机以加速度上升，当上升速度为时，有一螺丝自升降机的天花板上松脱，天花板与升降机的底面相距2.74m.计算：(1)螺丝从天花板落到底面所需要的时间;(2)螺丝相对升降机外固定柱子的下降距离. 

题解

第一问，求螺丝从天花板落到底面所需要的时间，这道题用非惯性参考系解决。先举一个例子来带入场景：人坐向上升的电梯时，会有身体沉重的感觉，即超重；这是因为此时人的加速度超过了正常的重力加速度，而人此时的加速度应该是等于重力加速度+电梯向上升的加速度。

这道题也是同理的，螺丝拥有的加速度也是等于重力加速度+升降机的加速度，所以很容易就可以求得时间了。

第二问，求螺丝相对于升降机外固定柱子的下降距离，原本来说，是会有三种情况的：

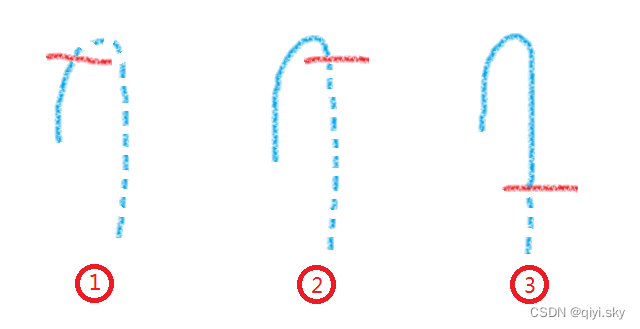
第一种情况是螺丝还没上升到最高点就被升降机拦截住了；第二种情况是螺丝已经上升到最高点，开始下落了被升降机拦截； 而第三种情况就是螺丝相对于一开始位置下降了之后被拦截了。

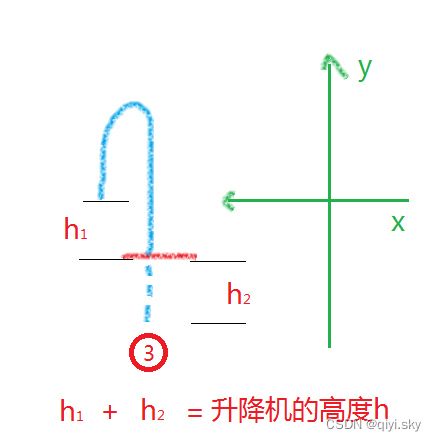
正常情况下，我们需要通过计算判断到底是哪种情况，但这道题目告诉我们了，是下降距离，所以我们就可以确定它是第三种情况了，根据第三种情况的情形进行列式。

4.动量定理

动量定理：在给定的时间间隔内，外力作用在质点上的冲量，等于质点在此时间内动量的增量。

动量：

冲量：

动量定理的微分形式： 

动量定理的积分形式：

分量表示：

题2

题目描述

一柔软链条长为，单位长度的质量为，链条放在有一小孔的桌上，链条一端由小孔稍伸下，其余部分堆在小孔周围。由于某种扰动，链条因自身重量开始下落。求：链条下落速度v与y之间的关系。设各处摩擦处均不计，且认为链条软得可以自由伸开。

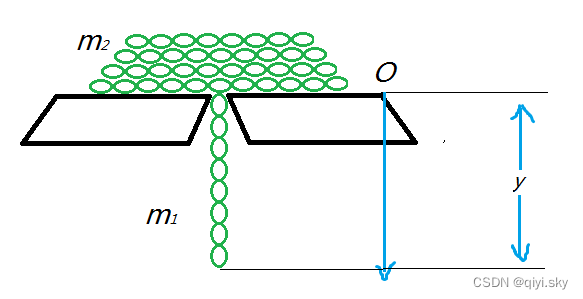
题解

以竖直悬挂的链条和桌面上的链条为一系统，建立坐标系，则

由质点系动量定理得：

故而有，

所以，

化简，整理得：

两边同时乘以，使之变成可积分的式子：

两边积分，得：

解得：

即，

5.动量守恒定律

动量守恒定律：若质点系所受的合外力为0，则系统的总动量不变。

• 系统的总动量不变，但系统内任一物体的动量是可以变的。
• 守恒条件：合外力为0.

注意：当时，即外力远远小于内力的作用时，可近似地认为系统总动量守恒。

题3

题目描述

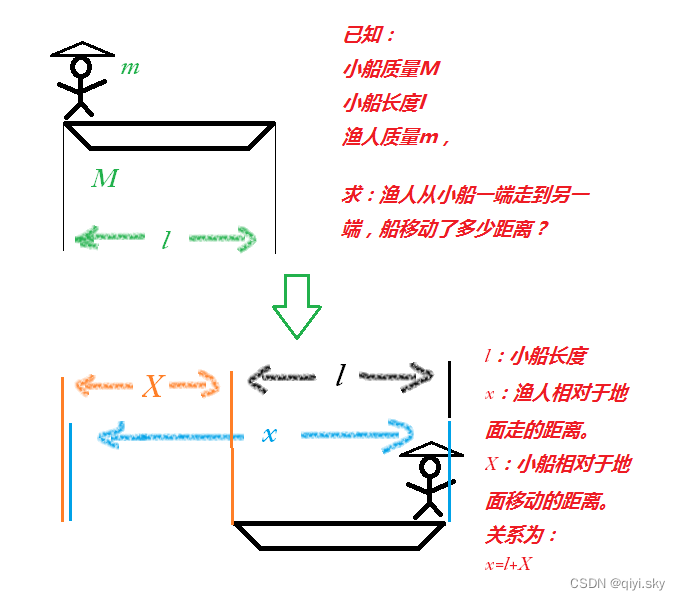
静止的湖面上有一条小船，长度为，质量为。船的一端站有一渔人，质量为。渔人和小船原来都静止不动。现设该渔人从船的一端走到另一端，问渔人和小船各移动了多少距离？水对船的摩擦可以忽略不计。

题解

由于水对船的摩擦可以忽略不计，所以人和小船这一系统沿水平方向上的合外力等于零，那么就可以应用动量守恒定律，得：

,表示人相对于地面的速度，表示船相对于地面的速度。

由上式可以得到：

表示小船与人反向运动。

人相对于小船的速度为：

设人时间内小船上走完船长，则有

这段时间内，人相对于地面走了：

结合两个积分式可以得到：

最终，小船移动的距离为：

，方向与人移动的方向相反。

如下图所示：

 

---

end 

---