推文作者:AmieeXue
第一部分 GAMS编程求解运输问题
GAMS,全称The General Algebraic Modeling System,是一款通用的高级数学建模工具,它支持线性规划、非线性规划、混合整数规划问题、二次约束规划(QCP)、二阶锥规划和混合整数二次约束规划(MIQCP)等问题的建模与求解。GAMS提供了独立的集成开发环境,也可以方便地与其他第三方求解器,如BARON、COIN-OR解算器、CONOPT、CPLEX、DIOPT、MOSEK、SNOPT、SULUM和XPRESS等,进行集成。由于这些优异的特性,GAMS被广泛地应用在电力系统、物流、交通及智能制造等行业领域。
运输问题模型
问题描述
已知工厂的供给量及市场对该单一商品的需求量,给定从工厂到市场的单位运输成本。试求每个工厂和每个市场之间应该有多少运输量才能最小化总运输成本?
数学模型
索引: i i i 表示工厂, j j j 表示市场
数据: a i a_i ai表示工厂 i 的商品供应量; b j b_j bj表示市场 j 对商品的需求量; c i j c_{ij} cij表示从工厂 i 到市场 j 的单位运输成本
决策变量: x i j x_{ij} xij表示从工厂 i 到市场 j 的运输量,显然它是一个正变量
目标:
m
i
n
:
∑
i
∑
j
c
i
j
∗
x
i
j
min: \sum_{i} \sum_{j} c_{ij}*x_{ij}
min:i∑j∑cij∗xij
约束:
∑
j
x
i
j
≤
a
i
,
∀
i
\sum_{j} x_{ij} \leq a_{i},\forall i
j∑xij≤ai,∀i
∑ i x i j ≥ b j , ∀ j \sum_{i}x_{ij} \geq b_{j}, \forall j i∑xij≥bj,∀j
注解:约束(2)表示工厂 i 的运输量不超过其生产能力;约束(3)表示市场 j 的运输量不小于其需求量。
基于GAMS的实现
这个简单的示例揭示了一些我们通常认为是良好习惯的建模实践,这些实践与 GAMS 的设计是一致的。
在GAMS中,采用的术语如下:指标称为sets,给定数据称为parameters,决策变量称为variables,约束和目标函数称为equations。
使用GAMS描述运输问题的方式与上述建模过程类似,只是它可以依靠计算机读取数据并进行处理的。下面我们给出算例数据和代码。运输问题的数据改编自(Dantzig, 1963),其中工厂与市场的运输距离单位为1000公里,每1000公里单位运输成本为90美元。 具体数据见下表:
| Plants ↓ | New York | Chicago | Topeka | ←Markets |
|---|---|---|---|---|
| Seattle | 2.5 | 1.7 | 1.8 | 350 |
| San Diego | 2.5 | 1.8 | 1.4 | 600 |
| Demands → | 325 | 300 | 275 | Supplies ↑ |
GAMS建模代码
Sets
i canning plants / seattle, san-diego /
j markets / new-york, chicago, topeka / ;
Parameters
a(i) capacity of plant i in cases
/ seattle 350
san-diego 600 /
b(j) demand at market j in cases
/ new-york 325
chicago 300
topeka 275 / ;
Table d(i,j) distance in thousands of miles
new-york chicago topeka
seattle 2.5 1.7 1.8
san-diego 2.5 1.8 1.4 ;
Scalar f freight in dollars per case per thousand miles /90/ ;
Parameter c(i,j) transport cost in thousands of dollars per case ;
c(i,j) = f * d(i,j) / 1000 ;
Variables
x(i,j) shipment quantities in cases
z total transportation costs in thousands of dollars ;
Positive Variable x ;
Equations
cost define objective function
supply(i) observe supply limit at plant i
demand(j) satisfy demand at market j ;
cost .. z =e= sum((i,j), c(i,j)*x(i,j)) ;
supply(i) .. sum(j, x(i,j)) =l= a(i) ;
demand(j) .. sum(i, x(i,j)) =g= b(j) ;
Model transport /all/ ;
Solve transport using lp minimizing z ;
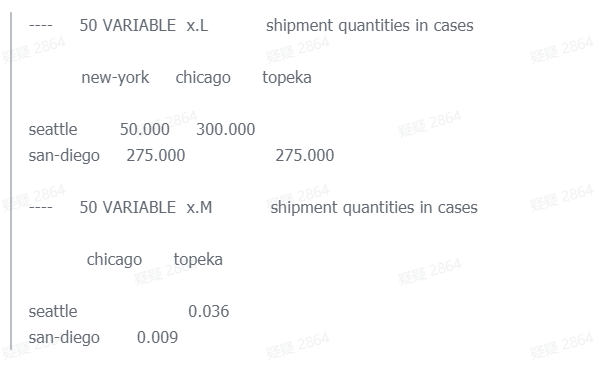
Display x.l, x.m ;
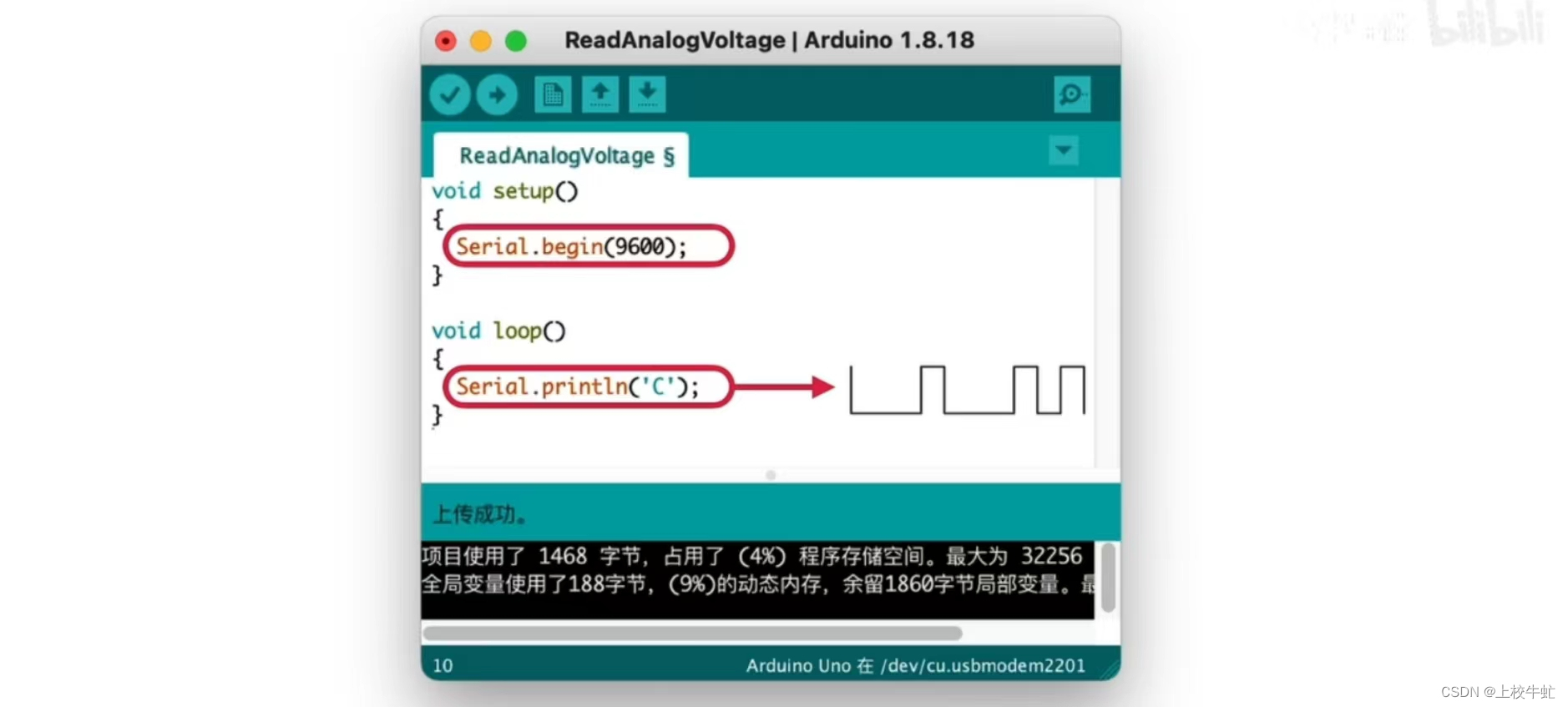
当你调用GAMS计算完毕,就会得到如下计算结果:
new-york chicago topeka
seattle 50.000 300.000
san-diego 275.000 275.000
你还可以得到单纯型乘子(边际成本):
chicago topeka
seattle 0.036
san-diego 0.009
结果显示,最好是从Seattle向Topeka运输,但是如果你增加一个单位的运输,将会增加0.036K的成本。
第二部分 GAMS建模的构成要素分析
GAMS的建模基本组件
在介绍单个组件之前,我们给出一些一般性评述。
- GAMS 模型是 GAMS 语言中语句的集合。控制语句顺序的唯一规则是模型的实体在声明存在之前不能被引用。
- GAMS 语句几乎可以以任何对用户有吸引力的样式进行排版。允许每条语句多行、嵌入空行和每行多条语句。
- 当您是 GAMS 的初级用户时,您应该像我们的示例中那样用分号终止每个语句。GAMS 编译器不区分大小写字母,因此您可以随意使用。
- 解释文档对于数学模型的有用性至关重要。如果将它嵌入模型本身而不是单独编写,它会更有用(并且最有可能是准确的)。至少有两种方法可以在 GAMS 模型中插入文档。首先,第 1 列中以星号开头的任何行都被 GAMS 编译器视为注释行。其次,可以在特定的 GAMS 声明中插入文档文本。
- GAMS 实体的创建涉及两个步骤:声明和赋值或定义。声明意味着声明某物的存在并为其命名。赋值或定义意味着赋予某物特定的值或形式。对于方程,您必须在单独的 GAMS 语句中进行声明和定义。但是,对于所有其他 GAMS 实体,您可以选择在同一语句中或单独进行声明和分配。
组成要素1:集合
定义集合以关键字Sets开头,在最后一个集合的结尾使用分号结尾。
- 一次性定义完所有集合
对于每个集合,首先给出集合的名称、关于集合的注释(可选)、集合元素赋值(放在 /…/ 中)
Sets i canning plants / seattle, san-diego /
j markets / new-york, chicago, topeka / ;
这句话的效果大概是不言而喻的。我们声明了两个集合并将它们命名为 i 和 j。我们还为集合分配了成员,如下所示:
i = {Seattle, San Diego}
j = {New York, Chicago, Topeka}.
注意:
•GAMS 使用斜杠 ‘/’ 而不是花括号 ‘{}’ 来描述集合,因为并不是所有的计算机键盘都有花括号键。
•当一个元素由多个单词构成时,应使用连接符,而不是空格。例如"New York",在代码中应表示为New-York
•代码中的注释文本不是必需的,它的作用是为了解释相关集合的含义,求解模型时这些文本并不会被使用。
- 每个集合单独定义
此外,没有必要将集合的创建全写在一个语句。我们可以将它们放入单独的语句中,如下所示:
Set i canning plants / seattle, san-diego / ;
Set j markets / new-york, chicago, topeka / ;
注意:在一个声明中使用 set ;和在一个声明中使用 sets 是等价的。
- 使用星号批量定义集合元素
将成员分配到集合时,使用星号会使建模变得简单。它适用于元素遵循顺序的情况。
例如,以下是 GAMS 中有效的 set 语句。
Set t time periods /1991*2000/;
Set m machines /mach1*mach24/;
它的实际含义是:
t = {1991,1992,1993, …, 2000}
m = {mach1, mach2, …, mach24}
请注意,集合元素存储为字符串,因此 t 的元素不是数字。
- 别名的定义与使用
另一个方便的功能是别名语句,它用于为先前声明的集合赋予另一个名称。在以下示例中:
Alias (t,tp);
名称 tp 就像数学符号中的 t’。它在关注同一集合内元素交互的模型中很有用。
组成要素2:数据
运输问题的 GAMS 模型展示了允许输入数据的几种不同格式。
- Lists的定义
定义参数以关键字Parameters开头,在最后一个参数的结尾用分号结尾;每个参数的定义需与已定义的集合对应,包含参数名、参数注释、参数赋值
Parameters a(i) capacity of plant i in cases
/ seattle 350
san-diego 600 /
b(j) demand at market j in cases
/ new-york 325
chicago 300
topeka 275 / ;
参数定义的解释:
•上述语句定义了 a 和 b 两个参数,它的定义域由前述定义的集合 i 和集合 j 确定。
•与集合的定义类似,每个参数的注释紧跟在参数定义的后面。
•接着,为每个参数的每个元素分配了响应的数值。
上面的语句也可以单独定义,对应的写法为:
Parameters a(i) capacity of plant i in cases / seattle 350 san-diego 600 / ;
Parameters b(j) demand at market j in cases / new-york 325 chicago 300 topeka 275/ ;
这里边涉及以下几个要点:
•每个元素由元素-值构成,且必需位于双斜线内部。
•GAMS有严格的域检查机制,确保列表中的成员是正确的。例如,集合 i 中的 Seattle,如果在这里错写成Seatle,会报错提示 指出元素“Seatle”不属于集合 i。
•每个参数定义完之后,必需使用分号分隔。
•所有参数的默认值为零,且只要元素位于集合中,它定义的顺序是任意的。例如,/seattle 350 san-diego 600/也可以写成/san-diego 600 seattle 350/.
- 定义标量
所谓标量,是指没有定义域的参数。可以使用包含只有一个值的退化列表的标量语句声明和赋值,如以下语句:
Scalar f freight in dollars per case per thousand miles /90/;
这行代码的意思是定义了一个常量 f,并将其赋值为90
- 定义表格
大型模型的许多输入数据来自相对较小的数字表。因此,具有用于数据输入的表格格式非常有用。下面提供了一个二维表(或矩阵)的例子:
Table d(i,j) distance in thousands of miles
new-york chicago topeka
seattle 2.5 1.7 1.8
san-diego 2.5 1.8 1.4 ;
该语句的作用是声明了一个表格d,它包含两个维度,第一个维度的索引来源于集合 i ,第二个维度的索引来源于集合 j 。与列表格式一样,GAMS 将执行域检查,以确保表的行和列名称是适当集合的成员。
- 直接赋值
在我们知道了每公里的运费和运输的公里数,就可以利用参数运算得到在两个城市之间的运输成本。那么可以使用下面的语句,来定义新的参数:
Parameter c(i,j) transport cost in thousands of dollars per case ;
c(i,j) = f * d(i,j) / 1000 ;
编写上述代码时,应该注意的要点是:
•代码包含两行,第一行是新参数的定义,第二行是新参数的赋值,两行代码都是以分号结尾的。第一行末尾的分号的必不可少的。没有它,GAMS 编译器会尝试将这两行解释为同一语句。
•上面第一条语句的作用是声明参数c,指定域(i,j),并提供一些文档解释。第二个语句将参数 f 和 d(i,j) 的值的乘积分配给 c(i,j)。能这么做的前提是您已经在前面的语句中为 f 和 d(i,j) 赋值。
•上面的直接赋值适用于 c 域中的所有 (i,j) 对。如果您希望对域中的特定元素进行分配,请将元素名称括在引号中。例如,c(‘Seattle’,‘New-York’) = 0.40;
•同一个参数可以被多次赋值,参数的最终值以最后一次赋值结果为准;但是,同一参数不能被声明多次,重复声明在 GAMS是一个语法错误,这样可以防止您不小心将相同的名称用于两个不同的事物。)
赋值语句的右侧可以包含各种各样的数学表达式和内置函数。但是,无论如何,都必须是左侧参数已在前面的语句中声明并且右侧参数已被赋值。以下是一些有效分配的示例。
csquared = sqr(c);
e = m*csquared;
w = l/lamda;
eoq(i) = sqrt( 2*demand(i)*ordcost(i)/holdcost(i));
t(i) = min(p(i), q(i)/r(i), log(s(i)));
euclidean(i,j) = qrt(sqr(xi(i) - xi(j) + sqr(x2(i) - x2(j)));
present(j) = future(j)*exp(-interest*time(j));
后面要介绍的求和、乘积运算符也可以用于直接赋值。
高纬度参数的使用方法,纬度之间使用 点号 分开:
Parameter salaries(employee,manager,department)
/ anderson .murphy .toy = 6000
hendry .smith .toy = 9000
hoffman .morgan .cosmetics = 8000 /;
组成要素3: 变量
在利用GAMS编写模型时,决策变量必须用变量语句声明。
- 变量声明
每个变量都有一个名称、一个域(如果合适)和(可选)文本。如下示例:
Variables
x(i,j) shipment quantities in cases
z total transportation costs in thousands of dollars ;
代码说明:
•此语句为每个 (i,j) 对声明一个运输变量。
•z 变量没有定义域,因为它是一个标量。每个 GAMS 优化模型都必须包含一个这样的变量作为要最小化或最大化的变量。这个变量的值就是我们想要的目标函数的值,它是一个自由变量。
- 变量类型
每个变量都必须分配一个类型,常见的变量类型有自由变量、非负变量、非正变量、二进制变量和整数变量。
| 变量类型 | 变量的取值范围 |
|---|---|
| free(default) | -inf to inf |
| positive | 0 to inf |
| negative | -inf to 0 |
| binary | 0 or 1 |
| binary | 0,1,2,…,100 (default) |
在我们的运输问题中,默认情况下 z 保持自由,但 x(i,j) 通过以下语句被限制为非负性。
Positive variable x ;
使用该语句,变量 x 中的所有元素都被定义为非负变量,我们不必要再为 x 中的每个元素再定义类型。
组成要素4: 模型约束和目标表达式
- 表达式声明
等式声明:表达式必须在单独的语句中声明和定义。声明的格式与其他 GAMS 实体相同。首先是关键字,在这种情况下是Equations,然后是一组或多组被声明的等式和不等式的名称、域和文本。我们的运输模型包含以下等式声明:
Equations
cost define objective function
supply(i) observe supply limit at plant i
demand(j) satisfy demand at market j ;
注意:在GAMS中,目标和约束表达式包含等式和不等式。
- 求和函数
GAMS提供了Sum函数来表示求和操作。Sum(求和索引, summand) 逗号分隔两个参数,如果第一个参数需要逗号,则应将其放在括号中。第二个参数可以是任何数学表达式,也可以包括另一个求和表达式。下面给出几个例子:
- 示例1:对单个维度求和
Sum(j, x(i,j))等价于\sum_{j}x_{ij} - 示例2:对两个维度求和
Sum((i,j), c(i,j)*x(i,j))等价于\sum_{i}\sum_{j}x_{ij}c_{ij}, - 示例3:嵌套求和,示例2中的两个维度的求和还可以写成
Sum(i, Sum(j, c(i,j)*x(i,j)))
此外,有时我们需要在求和时,排除一些元素,这一点可以通过调用美元运算符来事先。
- 求积函数
Prod在 GAMS 中使用与求和完全相同的格式定义。例如,prod(j, x(i, j)) 等价于 \prod_{j}x_{ij} 。
- 定义等式
方程定义是 GAMS 中最复杂的语句。方程定义的组成部分按顺序是: 方程的名称、符号"…"、左侧表达式、关系运算符(=l=, =e=, =g=)、右侧表达式。下面,我们给出一个示例:
cost .. z =e= sum((i,j), c(i,j)*x(i,j)) ;
supply(i) .. sum(j, x(i,j)) =l= a(i) ;
demand(j) .. sum(i, x(i,j)) =g= b(j) ;
定义方程需要注意以下要点:这里有一些要记住的要点。
•无论我们这里介绍的小例子,还是 20,000 个节点的现实世界问题,需求约束的定义都完全相同。因此,在任何一种情况下,用户只输入一个代数通用方程,GAMS 会创建适合手头模型实例的特定方程。
•关系运算符号:=l= 表示小于等于;=g=表示大于等于;=e=表示等于。
•要注意符号“=”和“=e=”是两个完全不同的符号,其中 “=”符号仅用于直接赋值,它只要是为参数赋值,不会包含任何决策变量;“=e=”符号仅用于方程定义,必需包含决策变量。
•变量可以出现在等式的左侧或右侧,或者两者都出现。同一个变量可以多次出现在方程中。 GAMS 处理器会在调用求解器之前自动将方程转换为其等效的标准形式。
•方程定义可以出现在 GAMS 输入中的任何位置,前提是方程及其引用的所有变量和参数事先声明。方程定义的顺序和声明的顺序可以不同。
组成要素5: 目标函数
在GAMS中,没有特地的定义关于目标函数的关键字,更不是一个独立的实体。在构建目标函数时,您必须创建一个变量,该变量是自由的(符号无约束)和标量值(无域),并且出现在方程定义中,将其等同于目标函数。
组成要素6 建模和求解语句
- 模型构建语句
模型,在GAMS中其实就是方程的集合。像其他 GAMS 实体一样,它必须在声明中给出一个名称。声明的格式是关键字Model,后跟模型名称,后跟用斜杠括起来的方程名称列表。
如果要包括所有先前定义的方程,则可以输入 /all/ 代替显式列表。在我们的示例中,有一个模型语句:
model transport /all/ ;
我们可以还使用显式列表而不是快捷方式 /all/,则语句将写为
model transport / cost, supply, demand / ;
特别提醒:GAMS允许在一次运行中定义多个模型,你可以以显示列表的形式定义多个包含不同目标和约束集的模型。
- 模型求解语句
一旦模型被声明并分配了方程,我们就可以调用求解器了。求解语句格式如下: 关键词solve 要求解的模型名称 关键字using 模型的类型 最大化、最小化 优化变量名。这是通过一个解决语句完成的,在我们的例子中写成:
solve transport using lp minimizing z ;
常见的模型类型如下:
| Solution | Description |
|---|---|
| lp | for linear programming |
| qcp | for quadratic constraint programming |
| nlp | for nonlinear programming |
| dnlp | for nonlinear programming with discontinuous derivatives |
| mip | for mixed integer programming |
| rmip | for relaxed mixed integer programming |
| miqcp | for mixed integer quadratic constraint programming |
| rmiqcp | for relaxed mixed integer quadratic constraint programming |
| minlp | for mixed integer nonlinear programming |
| rminlp | for relaxed mixed integer nonlinear programming |
| mcp | for mixed complementarity problems |
| mpec | for mathematical programs with equilibrium constraints |
| rmpec | for relaxed mathematical program with equilibrium constraints |
| cns | for constrained nonlinear systems |
| emp | for extended mathematical programming |
组成要素7 解的显示语句
为了获得原始和/或对偶变量的最佳值,我们可以查看求解器的输出;也可以让 GAMS 显示这些结果。在GAMS中,使用display关键字 变量名称.字段名,就可以获取我们感兴趣的信息。例如:
display x.l, x.m ;
GAMS 设计有一个小型数据库系统,其中保存变量和方程的记录。每条记录中最重要的字段是:
•.lo 表示下界
•.p 表示原始变量的值
•.up表示上届
•.m表示边际值或对偶变量的值
引用这些量的格式是变量或方程的名称后跟字段名称。
组成要素8 变量边界和/或初始值的分配
变量的下限和上限根据变量的类型(自由、正、负、二进制或整数)自动设置,但这些边界可以被 GAMS 用户覆盖。下面是一些例子。
x.up(i,j) = capacity(i,j) ;
x.lo(i,j) = 10.0 ;
x.up('seattle','new-york') = 1.2*capacity('seattle','new-york') ;
在第一个和第三个示例中假设 capacity(i,j) 是一个先前声明并赋值的参数。这些语句必须出现在变量声明之后和 Solve 语句之前。可用于直接赋值的所有数学表达式,都可以在右侧使用。
第三部分 输出报告的解读
GAMS的输出结果
GAMS 运行的默认输出包含了丰富的信息,用户可以根据这些输出信息,快速的修正自己的模型。
第一部分 导引文本
第一行是美元符号开头的模型提示性信息 $title a transportation model
第二部分 模型回显打印
从第2行开始,会原封不动的将你建立的模型打印出来。并且在左侧会显示行号,这样的话,你在排错误的时候,可以利用这些行号,快速定位到错误所在的行号信息。
第三部分 错误信息
当 GAMS 编译器在输入文件中遇到错误时,它会在紧跟犯罪现场的行上的回显打印中插入编码错误消息。这些消息总是以 开头,并在编译器认为发生错误的点正下方包含一个“$”。 美元符号后面是数字错误代码,在回显打印后进行解释。下面是几个例子:
- Example 1: 模型中使用了保留字
例如在表达式 set q quarterly time periods / spring, sos1, fall, wtr / ;,在回显打印中,报错为
1 set q quarterly time periods / spring, sos1, fall, wtr / ;
**** $160
在会显打印的底部,我们看到了错误代码 160 的解释:
Error Message
160 Unique element expected....
问题是sos1是保留字,一般不能作为标识符使用,这是一个常见的初学者错误。
- Example 2 : 模型缺少了必需的分号
另一个常见错误是在直接赋值或方程定义之前省略了分号。在我们的运输示例中,假设我们在分配 c(i,j) 之前省略了分号:
Parameter c(i,j) transport cost in 1000s of dollars per case
c(i,j) = f * d(i,j) / 1000 ;
此时会输出如下结果:
16 Parameter c(i,j) transport cost in 1000s of dollars per case
17 c(i,j) = f * d(i,j)/1000
**** $97 $195,96,409
Error Message
96 Blank needed between identifier and text
(-or- illegal character in identifier)
(-or- check for missing ';' on previous line)
97 Explanatory text can not start with '$', '=', or '..'
(-or- check for missing ';' on previous line)
195 Symbol redefined with a different type
409 Unrecognizable item - skip to find a new statement
looking for a ';' or a key word to get started again
仅仅丢掉一个分号,就会报出来4个错误,但是我们只需要重点关注第一个错误,因为你修改了这个错误,后面的错误可能也就不存在了。我们看到错误代码是97,表明 GAMS 认为第 17 行中的符号是第 16 行末尾文档文本的延续,而不是我们预期的直接赋值。该错误消息还适当地建议我们检查前一行是否缺少分号。
这里缺少了一个分号,GAMS很直接的发现了你的错误,并给出了解决方案。但是,您不能总是期望错误消息的建议中如此准确。有时编译器可能无法理解你的意图,所以要学会通过收集 GAMS 输出中大量的线索,来检测错误的原因。
- Example 3 : 拼写错误
许多错误仅仅是由拼写错误引起的。例如,表中“Seattle”的拼写与集合声明中的方式不同,我们会收到170号错误消息:
4 sets
5 i canning plants /seattle, san-diego /
6 j markets /new-york, chicago, topeka / ;
7
8 table d(i,j) distance in thousand of miles
9 new-york chicago topeka
10 seatle 2.5 1.7 1.8
**** $170
11 san-diego 2.5 1.8 1.4 ;
Error Message
170 Domain violation for element
同样,如果我们错误地输入 dem(j) 而不是 b(j) 作为需求约束的右侧,结果是
45 demand(j) .. sum(i, x(i,j) ) =g= dem(j) ;
**** $140
Error Message
140 Unknown symbol
第四部分 引用地图
它紧跟在错误信息之后,其中包含输入文件的摘要和分析,用于调试和记录。
- 交叉引用地图
第一个参考地图是交叉引用地图(cross-reference map),它是模型的所有实体(集合、参数、变量和方程)的按字母顺序排列的交叉引用列表。该列表显示了每个实体的符号、类型和引用次数。我们的运输问题示例的交叉参考地图如下(我们不显示所有表格)。要打开引用地图地图,需在模型中添加如下代码:
$onSymXRef
由此,GAMS输出的引用地图如下:
- SYMBOL TYPE REFERENCES
a PARAM declared 9 defined 10 ref 42
b PARAM declared 13 defined 14 ref 44
c PARAM declared 25 assigned 27 ref 40
cost EQU declared 36 defined 40 impl-asn 48
ref 46
d PARAM declared 18 defined 18 ref 27
demand EQU declared 38 defined 44 impl-asn 48
ref 46
f PARAM declared 23 defined 23 ref 27
i SET declared 4 defined 4 ref 9
18 25 27 30 37 240
242 44 control 27 40 42
44
j SET declared 5 defined 5 ref 13
18 25 27 30 38 240
42 244 control 27 40 42
44
supply EQU declared 37 defined 42 impl-asn 48
ref 46
transport MODEL declared 46 defined 46 impl-asn 48
ref 48
x VAR declared 30 impl-asn 48 ref 33
40 42 44 2*50
z VAR declared 31 impl-asn 48 ref 40
48
关于引用地图的一些注解:
- 符号a
- 在第9行声明 (declared)
- 第10行定义(defined)
- 第42行引用(ref)
- 集合 i
- 在第4行声明 (declared)
- 第4行定义(defined)
- 在 10, 19, 26, 28, 31, 38, 45行被引用,其中41行和43行被引用两次;(ref)
- 在第 28、41、43 和 45 行中,集合 i 还用作求和、方程定义或直接参数分配中的控制索引(control)。
对于GAMS新手来说,交叉引用列表的详细分析可能并不重要。也许他或她从引用地图中获得的最有可能的好处是发现了由于标点符号或语法错误而错误地进入模型的不需要的实体。
- 按类型划分的实体列表
参考地图的第二部分是按类型分组的模型实体列表,并列出了它们相关的文档文本。例如:
- SETS
i canning plants
j marketsPARAMETERS
a capacity of plant i in cases
b demand at market j in cases
c transport cost in thousands of dollars per case
d distance in thousands of miles
f freight in dollars per case per thousand milesVARIABLES
x shipment quantities in cases
z total transportation costs in thousands of dollarsEQUATIONS
cost define objective function
demand satisfy demand at market j
supply observe supply limit at plant iMODELS
transport
第五部分 方程列表
一旦您成功构建了一个没有编译错误的输入文件,GAMS 就能够生成一个模型。 方程式列表相当于将模型完整的导出。作为solve 命令的产物,方程列表显示了当集合和参数的当前值插入模型的一般代数形式时创建的模型的特定实例。
例如,运输模型的输入文件中给出的通用需求约束是:
demand(j) … sum(i, x(i,j)) =g= b(j) ;
会生成如下方程式列表:
--------demand =g= satisfy demand at market j
demand(new-york)… x(seattle, new-york) +x(san-diego, new-york) =g= 325 ;
demand(chicago)… x(seattle, chicago) +x(san-diego, chicago ) =g=
300 ;
demand(topeka)… x(seattle, topeka) +x(san-diego, topeka) =g=
275 ;
对于每个通用方程,默认输出最多为三个特定方程。要更改默认值,请在求解语句之前插入输入语句:
option limrow = r ;
其中 r 是所需的数字。要更改每个通用变量的特定列打印输出的默认数量,可以扩展上述命令:
option limrow = r, limcol = c ;
其中 c 是所需的列数。注意,在模型调试完毕后,将 limrow 和 limcol 设置为 0 ,是减小 lst 文件大小的好方法。
在非线性模型中,GAMS 方程列表显示非线性方程的一阶泰勒近似。
第六部分 模型的统计信息
- GAMS 在调用求解器之前,生成的最后一部分输出是,关于模型规模的一组统计信息,如下面的运输案例:
MODEL STATISTICS
BLOCKS OF EQUATIONS 3 SINGLE EQUATIONS 6
BLOCKS OF VARIABLES 2 SINGLE VARIABLES 7
NON ZERO ELEMENTS 19
这些信息告诉我们,模型中包含3个等式块,6个单独的等式,2个变量块,7个单独的变量和19个非零元素。
对于非线性模型,给出了一些其他统计量来描述问题中的非线性程度。
第七部分 模型的状态报告
求解器执行后,GAMS 打印出一个简短的求解摘要,其中两个最重要的条目是求解器状态和模型状态。对于我们的运输问题,解决摘要如下:
S O L V E S U M M A R YMODEL TRANSPORT OBJECTIVE z
TYPE LP DIRECTION MINIMIZE
SOLVER CPLEX FROM LINE 49
- SOLVER STATUS 1 Normal Completion
- MODEL STATUS 1 Optimal
**** OBJECTIVE VALUE 153.6750RESOURCE USAGE, LIMIT 0.031 1000.000
ITERATION COUNT, LIMIT 4 2000000000
报告解读:
- 求解器状态:状态报告前面有与错误消息相同的 字符串,因此您应该养成在第一次查看输出文件时搜索所有出现此字符串的习惯。所需的求解器状态为 1 NORMAL COMPLETION,但还有其他可能性,记录在“求解摘要”部分。
- 模型状态:有 11 种可能的模型状态,包括通常的线性规划终止状态(1 最佳、3 无界、4 不可行),以及其他与非线性和整数规划相关的状态。
- 在非线性规划中,要查找的状态是 2 局部最优。对于非线性规划,软件最多可以保证是局部最优。用户负责分析问题的凸性,以确定局部最优性是否足以满足全局最优性。
- 在整数规划中,要查找的状态是 8 Integer Solution。这意味着已经找到了一个可行的整数解。有关解决方案是否满足用户指定的相对和绝对最优容差的更多详细信息如下。
第八部分 解决方案报告
如果求解器状态和模型状态是你所期望的,就可以愉快地查看结果了。结果以标准数学输出格式呈现,并添加了根据适合刚刚求解的特定模型的名称对行和列进行分组和标记的附加功能。在这种格式中,每一行和每一列都有一行打印输出,给出了下限、级别、上限和边际。通用方程块和列输出按通用变量块对行输出进行分组。设置元素名称嵌入在输出中以便于阅读。
- 详细报告
在运输示例中,供应 (i)、需求 (j) 和 x(i,j) 的求解器输出如下:

输出信息的一些解释:
- 单点“.”在输出中代表零。epsilon 显示为 EPS, 表示非常小但非零;在这种情况下,EPS 表示退化。 (西雅图供应约束的松弛变量在零水平的基础上。边际用 EPS 而不是零标记,以方便从旧基础重新启动优化器。)
- 如果求解器结果包含错误符号的不可行性或边际成本,则违规条目分别标记为 INFES 或 NOPT。
- 如果问题无界终止,则对应于极方向的行和列标记为 UNBND。
- 报告摘要
在求解器解决方案报告的末尾是一个非常重要的报告摘要,它给出了非最优、不可行和无界行和列的总数。对于我们的示例,报告摘要根据需要显示所有零计数。
**** REPORT SUMMARY : 0 NONOPT
0 INFEASIBLE
0 UNBOUNDED
- 用户指定信息的显示
求解器获得的所有值和边际,都在 .l 和 .m 字段中输入到 GAMS 数据库中。然后可以转换这些值并将其显示在任何所需的报告中。如前所述,用户仅列出要显示的数量,GAMS 会自动格式化并标记适当的数组。例如,输入语句:
display x.l, x.m ;
有如下输出:
总结
本教程展示了 GAMS 的几个设计特性,使您能够快速有效地构建实用的优化模型。以下讨论总结了使用代数建模语言(例如 GAMS)与矩阵生成器或对话式求解器的优势。
- 由于对问题的代数描述具有普遍性,因此当出现相同或相关问题的新实例时,GAMS 模型中的大多数语句都是可重用的。这在模型不断变化的环境中尤为重要。
- 通过在一个语句中创建一整套密切相关的约束,可以节省时间并减少生成错误。
- 可以通过提供用于计算数据的公式而不是明确输入它们,来节省时间并减少输入错误。
- GAMS 的输出用起来很方便直观。来自求解器的解决方案报告会自动重新格式化,以便将相关方程和变量组合在一起并适当标记。
- GAMS检测错误的数百种方法也应该会大大缩短开发时间。
本教程中暂未涉及美元运算符和其他高级功能,美元运算符的具体应用包括:
- 它可以对要包含在模型中的变量和方程的索引的组合逻辑进行限制,从而筛选出不需要的行和列,并将问题的大小保持在可解决范围内。
- 它可用于构建复杂的求和和求积。
- 它可用于发出警告消息或根据特定于上下文的数据编辑提前终止。