分类目录：《深入理解深度学习》总目录

相关文章：
·注意力机制（AttentionMechanism）：基础知识
·注意力机制（AttentionMechanism）：注意力汇聚与Nadaraya-Watson核回归
·注意力机制（AttentionMechanism）：注意力评分函数（AttentionScoringFunction）
·注意力机制（AttentionMechanism）：Bahdanau注意力
·注意力机制（AttentionMechanism）：多头注意力（MultiheadAttention）
·注意力机制（AttentionMechanism）：自注意力（Self-attention）
·注意力机制（AttentionMechanism）：位置编码（PositionalEncoding）

---

在处理词元序列时，循环神经网络是逐个的重复地处理词元的，而自注意力则因为并行计算而放弃了顺序操作。 为了使用序列的顺序信息，通过在输入表示中添加位置编码（Positional Encoding）来注入绝对的或相对的位置信息。 位置编码可以通过学习得到也可以直接固定得到。 接下来描述的是基于正弦函数和余弦函数的固定位置编码。

假设输入表示$X\in R^{n\times d}$包含一个序列中$n$个词元的$d$维嵌入表示。 位置编码使用相同形状的位置嵌入矩阵$P\in R^{n\times d}$输出$X+P$， 矩阵第$i$行、第$2j$列和$2j+1$列上的元素为：
$$\begin{array}{rl}{p}_{i,2j}& =\sin (\frac{1}{10000^{\frac{2j}{d}}})\\ p_{i,2j+1}& =\cos (\frac{1}{10000^{\frac{2j}{d}}})\end{array}$$

在位置嵌入矩阵$P$中，行代表词元在序列中的位置，列代表位置编码的不同维度。从下面的例子中可以看到位置嵌入矩阵的第6列和第7列的频率高于第8列和第9列。 第6列和第7列之间的偏移量及第8列和第9列之间的偏移量正是由于正弦函数和余弦函数的交替。

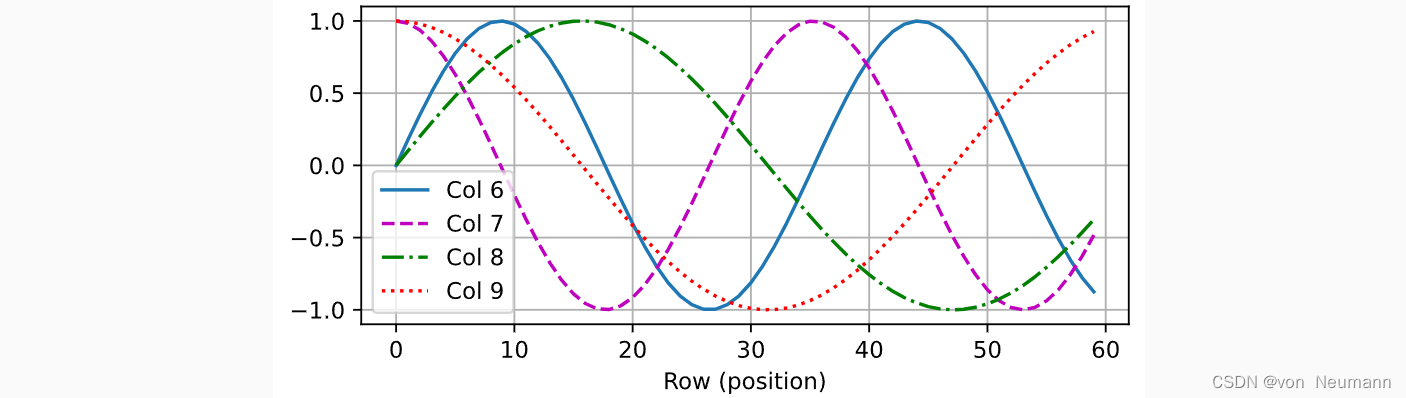
绝对位置信息

为了明白沿着编码维度单调降低的频率与绝对位置信息的关系， 下面是$0,1,\cdots ,7$的二进制表示形式。正如所看到的，每个数字、每两个数字和每四个数字上的比特值在第一个最低位、第二个最低位和第三个最低位上分别交替。

0的二进制是：000
1的二进制是：001
2的二进制是：010
3的二进制是：011
4的二进制是：100
5的二进制是：101
6的二进制是：110
7的二进制是：111

在二进制表示中，较高比特位的交替频率低于较低比特位， 与下面的热图所示相似，只是位置编码通过使用三角函数在编码维度上降低频率。 由于输出是浮点数，因此此类连续表示比二进制表示法更节省空间。

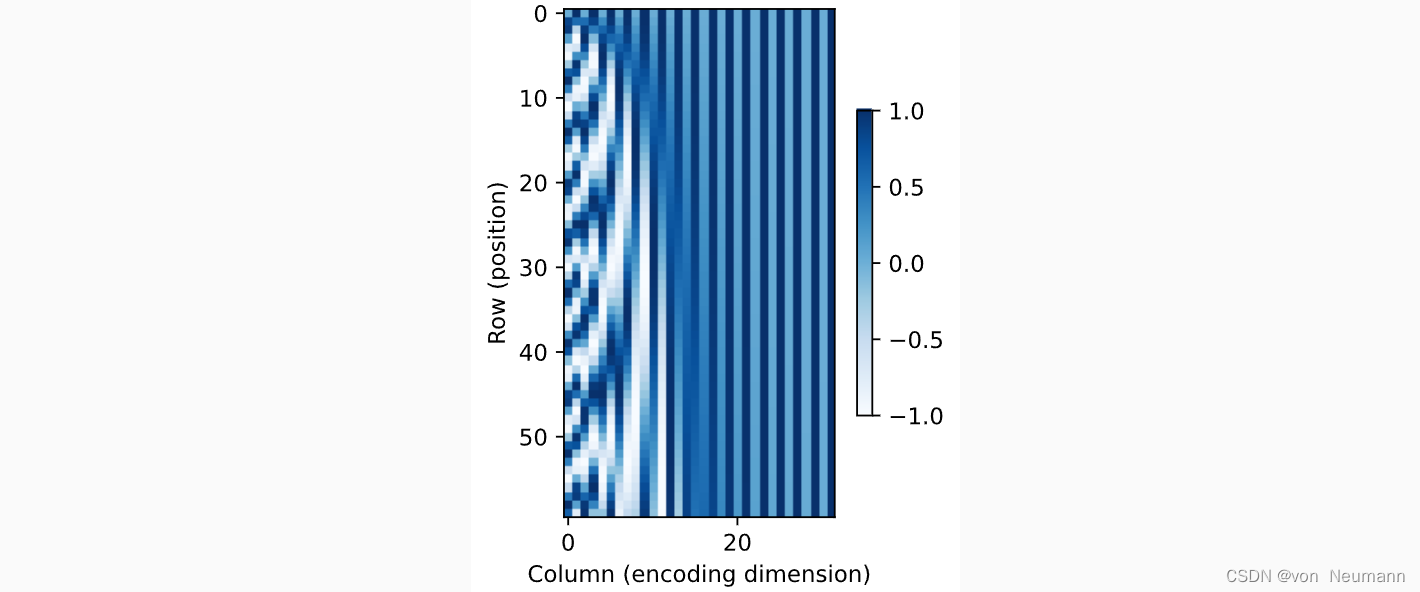
相对位置信息

除了捕获绝对位置信息之外，上述的位置编码还允许模型学习得到输入序列中相对位置信息。 这是因为对于任何确定的位置偏移$\delta$，位置$i+\delta$处的位置编码可以线性投影位置$i$处的位置编码来表示。

这种投影的数学解释是，令$w_j=\frac{1}{10000^{\frac{2j}{d}}}$， 对于任何确定的位置偏移$\delta$，任何一对$(p_{i,2j},p_{i,2j+1})$都可以线性投影到 $(p_{i+\delta ,2j},p_{i+\delta ,2j+1})$：

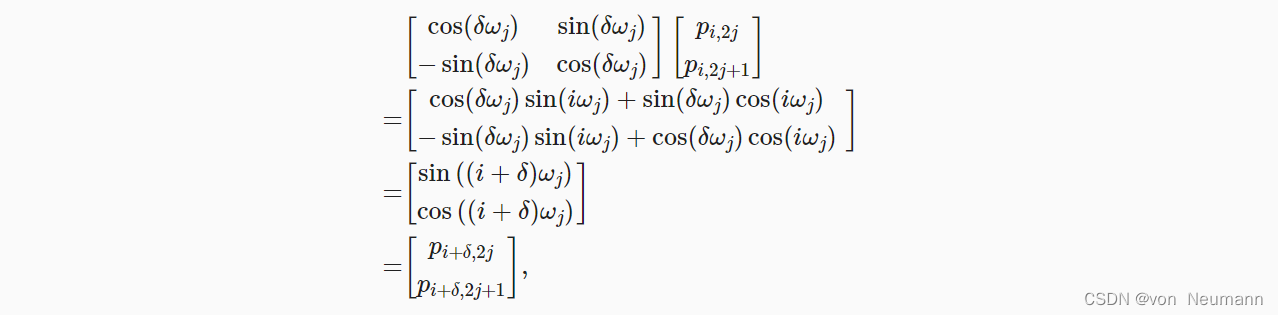
参考文献：
[1] Lecun Y, Bengio Y, Hinton G. Deep learning[J]. Nature, 2015
[2] Aston Zhang, Zack C. Lipton, Mu Li, Alex J. Smola. Dive Into Deep Learning[J]. arXiv preprint arXiv:2106.11342, 2021.