题目描述
给定一个序列,使用该序列生成二叉排序树(也叫二叉搜索树,BST),然后以本题规定方法输出该二叉排序树。
例:
给定一个序列:43 25 29 67 17 88 54 47 35 62
以第一个数字(43)为根节点,然后将后面的数字依输入次序逐个添加至该树中,得到一个二叉排序树,如下图所示。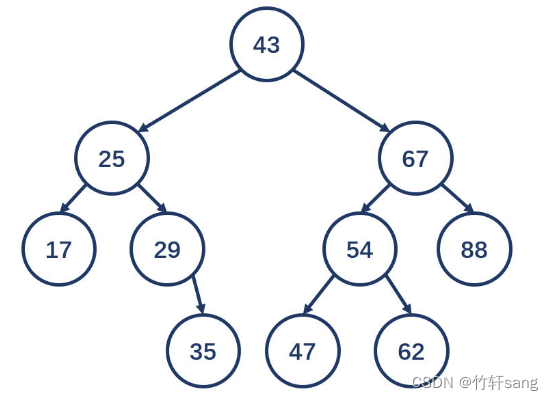
然后先序遍历上面这个树,并按行输出数字。
其中每个子节点的输出前,需要相较于其父节点前多四个普通空格。
当某个节点为叶子节点(即无子节点),则该节点的左右叶子节点均不用输出。
而当某个节点仅有左叶子节点或右叶子节点时,另一个空缺的子节点用#占位。
以该图为例,其最终输出结果为:
43
25
17
29
#
35
67
54
47
62
88
输入格式
第一行为正整数n,表示接下来将输入的节点数量。(n<500)
第二行为n个正整数,每个数字以空格分隔(以第一个数字为根节点)
输出格式
以题目描述中的方法输出得到的二叉排序树。
以第一个数字为根节点,然后将后面的数字依输入次序逐个添加至该树中,得到一个二叉排序树。
然后先序遍历该树,并按行输出数字。
其中每个子节点的输出前,需要相较于其父节点前多四个普通空格。
当某个节点为叶子节点(即无子节点),则该节点的左右叶子节点均不用输出。
而当某个节点仅有左叶子节点或右叶子节点时,另一个空缺的子节点用#占位。
输入样例
10
43 25 29 67 17 88 54 47 35 62输出样例
43
25
17
29
#
35
67
54
47
62
88代码展示
注意题目要求的输出格式
#include<iostream>
#include<bits/stdc++.h>
#include<vector>
#include<utility>
#include<climits>
using namespace std;
struct BiNode{
BiNode(int aKey){
key=aKey;
lchild=rchild=nullptr;
}
int key;
BiNode *lchild,*rchild;
};
using BiTree=BiNode*;
int InitBiTree(BiTree &T){
T=nullptr;
return 0;
}
int Insert2(BiTree &T,int aKey){
//定位插入位置
BiNode **p=&T;
while(*p!=nullptr&&(*p)->key!=aKey){
p=aKey<(*p)->key?&(*p)->lchild:&(*p)->rchild;
}
if(*p!=nullptr)
return 1;
//插入新结点
*p=new BiNode(aKey);
return 0;
}
//test
int InTraverse(BiTree T){
if(T==nullptr) return 0;
InTraverse(T->lchild);
cout<<T->key<<" ";
InTraverse(T->rchild);
return 0;
}
string s="";
void InorderTree(BiTree T){
cout<<s;
if(T){
cout<<T->key<<" ";
cout<<endl;
if(T->lchild||T->rchild){
s+=" ";
InorderTree(T->lchild);
InorderTree(T->rchild);
for(int i=0;i<4;i++) s.pop_back();
}
}
else{
cout<<"#"<<endl;
}
}
int main(){
//freopen("/config/workspace/test/test","r",stdin);
int n;
cin>>n;
int a[n];
for(int i=0;i<n;i++){
cin>>a[i];
}
BiTree T;
InitBiTree(T);
for(int i=0;i<n;i++){
Insert2(T,a[i]);
}
//InTraverse(T);
InorderTree(T);
return 0;
}//闲叙题外话:好奇妙的感觉...!