在常用的数据结构中，有一批结构被称为容器——栈与队列。

本篇博客主要学习一下栈这种结构的特性，以及用python实现它的相关操作。

内容

1. 顺序栈
2. 链栈
3. 栈的实际应用

在这之前，我们需要了解一下什么是栈，以及栈这种结构有什么用处？

🍁 顺序栈

🍃 理解

定义：
前面说到，栈相对于是一个容器，而这个容器里包含的是一些元素（这些元素的数据类型可以整型、浮点型、字符型等）。
同时，栈是保证元素后进先出关系的结构。例如，我们把几本书叠在一起，最上面的书也就是最后放上去的，我们要拿最下的面的书也只有先拿最上面的书，这满足了栈这种“后放先拿”的特性；又例如，做数学题时，遇到推导进行不下去的时候，我们通常是退回一步去考虑其它的可能性。

作用：
栈主要用来保存计算过程中的临时数据，这些数据是计算中发现或者产生的，在后面的计算中可能需要使用到它们。
栈也常常用来作为一种缓冲存储结构，用来存储工作中产生的暂时不用或者用不完的数据。

操作：
压栈：把数据压入栈
弹栈：把数据弹出栈

下面用一张图来说明栈的操作：

在Python中，我们可以用list来实现顺序栈，由于list才用动态顺序表技术，用它作为栈的表不会满，同时，python的内置函数append()和pop()也可以完美实现压栈和弹栈的操作。

因为用C语言刷过一遍数据结构，在这里呢，我就用两个指针来完成压栈和弹栈的操作。
base：栈底指针，始终指向栈底元素，一直不变。
top：栈顶指针，始终指向栈顶元素的后面。

请结合下图理解：

🍃 操作

🍂 定义

class stack:
    def __init__(self, maxsize):
        self.max = maxsize              # 栈的最大容量
        self.elem = [None] * self.max   # 用list数据类型来表示顺序栈
        self.top = 0                    # 栈顶指针
        self.base = 0                   # 栈底指针

🍂 压栈

    def push(self,elem):
        if self.top - self.base == self.max:            # 判断栈是否已满
            raise Exception("The stack is full!")
        self.elem[self.top] = elem                      # 元素入栈
        self.top += 1                                   # top指针指向栈顶元素的下一个

🍂 弹栈

    def pop(self):
        if self.top == self.base:
            raise Exception("The stack is empty")       # 判断栈是否已空
        self.top -= 1                                   # top指向栈顶元素（牢记top指针的定义:top始终指向“栈顶元素”的后面）
        e = self.elem[self.top]                         # 用e接收弹出的元素
        return e  

🍂 取栈顶元素

    def get_top(self):
        return self.elem[self.top - 1]

🍂 验证顺序栈的操作

data = list(map(int,input("Please input a series of datas:").split(" ")))

s = stack(len(data))            # 栈的初始化
for i in range(len(data)):      # 将元素压栈
    s.push(data[i])
for i in range(s.top - s.base): # 输入栈内元素
    print(s.elem[i],end=" ")

print("\n")

e = s.get_top()
print("The top elem of the stack is: %d" % e)	# 栈顶元素是：

print("\n")

for i in range(s.top - s.base): # 弹栈
    s.pop()     # 弹一次栈
    print("After popping the stack %d times,the stack is:" % (i + 1),end=" ")
    for j in range(s.top - s.base): # 输出每次弹栈后，栈内剩余的元素
        print(s.elem[j],end=" ")
    print("\n")

执行结果如下：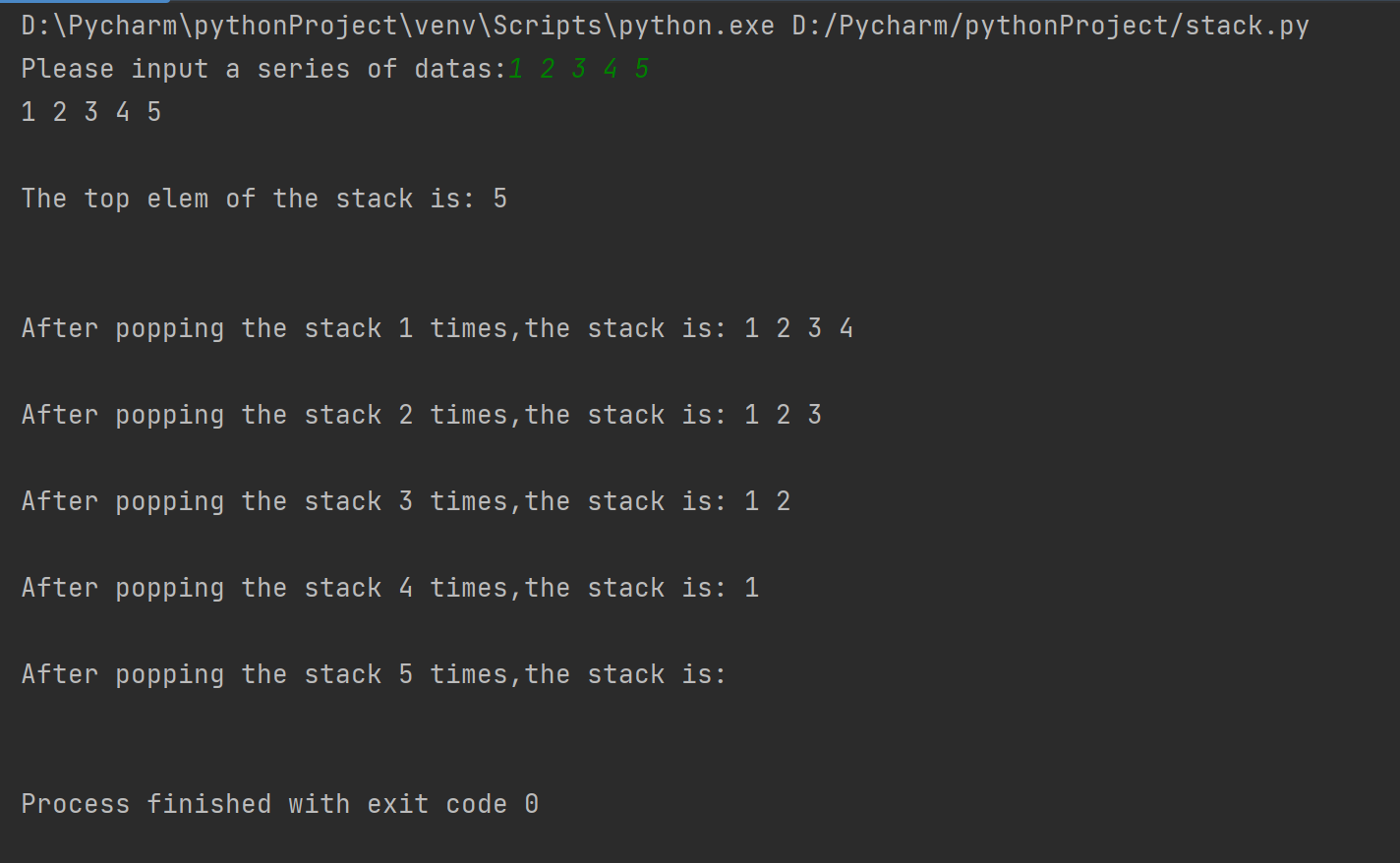

🍁 链栈

🍃 理解

在顺序栈中，一个栈的大小是固定死了的，为了实现栈的空间的动态增减，我们下面引入链栈。

链栈相当于是将前面的顺序栈中的每个元素拆分开来，从一个大的整体变成一个一个的小部分，然后再用某种方式将这些小部分链接起来，如下图所示：

其中，“某种链接方式”就相当于是C语言里的指针，用指针来链接每个“小部分”。link_top为链栈的栈顶指针，始终指向栈顶元素（注意与顺序栈中的栈顶指针作区分）。

那么为了实现链栈，我们需另设一个“结点类”来存储每个结点的信息，由上面的叙述可知，一个结点应该包含数据域（存放东西的地方）和指针域（链接方式，用于实现结点之间的链接）。

🍃 操作

🍂 定义

class stacknode:					# 结点类
    def __init__(self):
        self.elem = None			# 数据域
        self.next = None			# 指针域

class link_stack:					# 链栈类
    def __init__(self):
        self.link_top = None        # 链栈的指针，指向栈顶元素

🍂 压栈

关于链栈的压栈，它的方法本质上跟链表的头插法是一样的。

    # 压栈（头插法）
    def link_push(self,elem):
        s = stacknode()             # 生成一个新结点
        s.elem = elem               # 填充结点的值
        s.next = self.link_top      # 该结点指向下一个结点
        self.link_top = s           # 指针移动，指向栈顶元素

结合下图理解：

图中的s代表新生成的结点

🍂 弹栈

    # 弹栈
    def link_pop(self):
        e = self.link_top.elem              # 记录弹栈的那个结点
        self.link_top = self.link_top.next  # 栈顶指针指向下一个结点
        return e                            # 返回弹栈的那个结点

🍂 获取链栈的长度

    def get_length(self):
        top = self.link_top                 # 用top来代替link_top移动
        count = 0                           # 计数器
        while top is not None:
            count += 1                      # 栈顶指针不为空，则加1
            top = top.next                  # 指针指向下一个结点
        return count                        # 返回count

🍂 获取栈顶元素

    def get_top(self):
        if self.link_top == None:
        	return None
        return self.link_top.elem

🍂 验证链栈的操作

s = link_stack()	# 链栈的初始化
data = list(map(int,input("Please input a series of datas:").split(" ")))   # 输入数据
for i in range(len(data)):          # 将data中的数据依次压栈，压栈顺序为1->2->3->4->5
    s.link_push(data[i])

top = s.link_top    # 用top代替link_top移动
print("The sequence of the datas in stack is:",end=" ") # 按先进后出的顺序输出链栈中的数据
while top is not None:		# 依次输出链栈中每个结点的值
    print(top.elem,end=" ")
    top = top.next
print("\n")

for i in range(s.get_length()):     # 按先进后出的顺序，输出每一次弹栈后链栈中的数据
    s.link_pop()    # 弹栈
    print("After popping the stack %d times,the stack is:" % (i + 1),end=" ")
    top = s.link_top
    while top is not None:
        print(top.elem,end=" ")
        top = top.next
    print("\n")

执行结果如下：

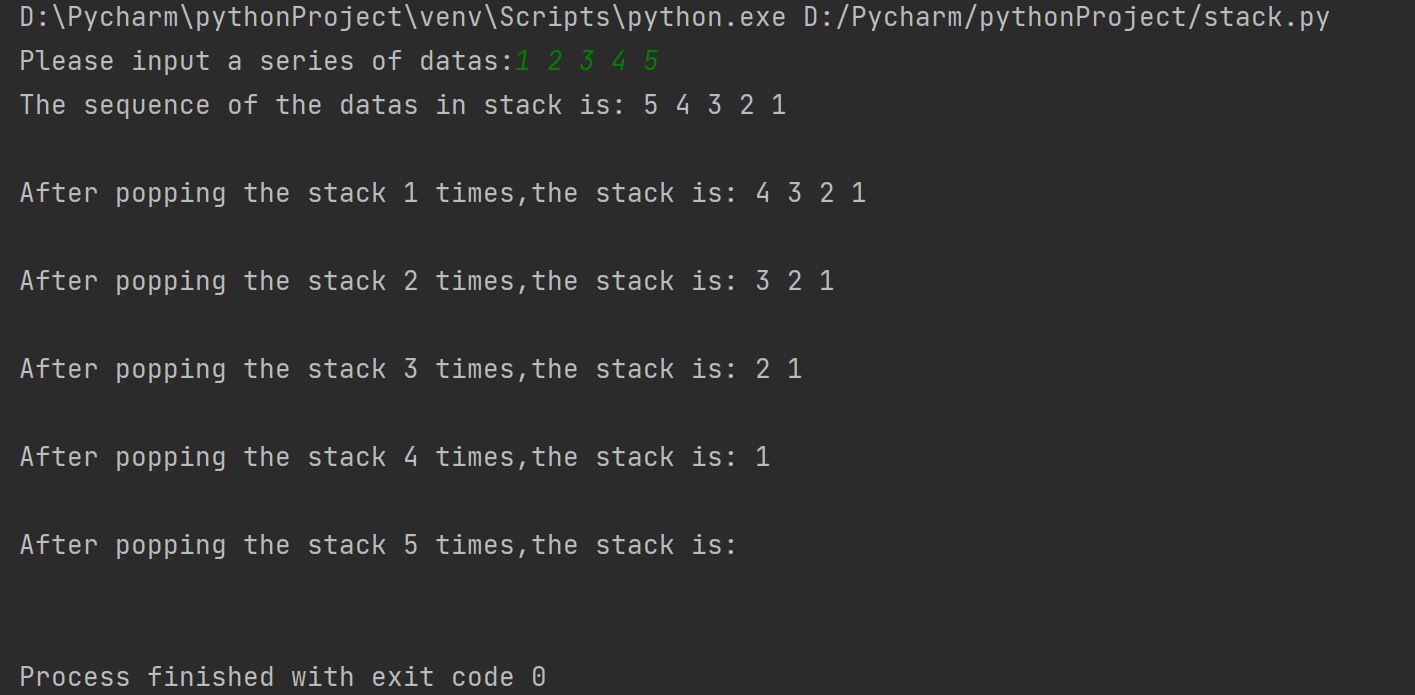
🍁 栈的实际应用

其实在前面验证顺序栈、链栈的操作时，我们已经完成了一个小小的应用，也就是颠倒一组元素的顺序。只需把所有元素按原来的顺序全部压栈，再依次弹栈，就能得到反序后的序列。

对于栈的应用，我们先从最简单的非递归应用开始。

🍃 栈与递归

先看一个关于阶乘的递归函数

def factorial(n):
    if n == 0:
        return 1
    else:
        return n * factorial(n - 1)

0的阶乘是1。

可以看到，在函数中这个递归过程就是一个“层层包围”的过程，是由里向外的一个计算过程。就像这个算式“(1+(2+(3+(4+5))))”一样，它总是先计算最里面的括号，然后一步一步地向外计算。

在程序执行时，函数的嵌套调用是按“后调用先返回”的规则进行，这种规则符合栈的使用模式，因此栈可以很自然地支持函数调用的实现。

下面给出用栈实现阶乘的算法：

def factorial_stack(n):
    res = 1							# 保留阶乘的结果
    st = link_stack()
    while n > 0:					# 先将需要计算的对象压栈
        st.link_push(n)
        n -= 1
    while st.get_length() != 0:		# 然后开始阶乘的计算
        res *= st.link_pop()
    return res

当然这只是列举了一个简单的例子，大家可自行用栈去实行其它复杂的过程

🍃 括号匹配问题

什么是括号匹配？

首先在这个问题中，我们只考虑三种括号，分别是：() [] {}。并命名“(”、“[”、“{”为开括号，“)”、“]”、“}”为闭括号。

所谓括号匹配，就是将开括号与闭括号匹配，也就是每对括号的开括号一定要在闭括号前，就算匹配成功。例如：
() 匹配成功
[()] 匹配成功
({[]}) 匹配成功
()[]{} 匹配成功
[) 匹配失败
{(]} 匹配失败

如何利用栈解决这个问题？

它的一个主要思想就是逐个处理遇到的括号，遇到开括号就直接进栈，遇到闭括号时与栈顶元素比较，若这俩是一对就将栈顶元素出栈，然后继续往下处理；若这俩不是一对，就说明匹配失败了。

由前面我们可以看到，匹配成功的情况有两种，一种是一对括号包围着另一对括号，就像([])一样；另一种就是一对括号接另一对括号，例如()[]。其实这个就跟“消消乐”差不多，第一种情况也就是由内向外消除，第二种情况就是依次消除。

在python中，“匹配”两个字是非常敏感的，因为字典这种数据结构不正好符合“匹配”的含义吗？所以，我们可以利用字典的特性来解决这个问题。下面上代码：

# 这里用的是链栈
def check(s):
    brackets = {")": "(", "]": "[", "}": "{"}       # 字典，用来当作判断的条件
    open_bracket = "([{"                            # 用来逐个判断字符是否为开括号

    length = len(s)          # 获取字符串长度
    if length % 2 == 1:      # 因为括号一定成对出现，所以出现奇数个括号时一定不匹配
        return False

    st = link_stack()                              # 链栈初始化
    for i in range(length):                        # 进入循环
        if s[i] in open_bracket:                   # 逐个判断字符是否为开括号
            st.link_push(s[i])                     # 若为开括号就进栈
        else:                                      # 若不为开括号，那么就是闭括号，进入else
            if brackets[s[i]] == st.get_top():     # 若该闭括号与栈顶元素相匹配
                st.link_pop()                      # 将栈顶元素出栈
            else:                                  # 若不匹配
                return False                       # 则整个字符串就不匹配
    if st.get_length() != 0:                       # 如果匹配成功，栈里此时一定没有元素，如果有，那么一定匹配失败
        return False    
    return True       							   # 执行到此处，说明不匹配的条件已全部排除，所以匹配成功

测试代码：

# 这里需要导入random包
import random
pairs = "()[]{}"                    # 定义括号集

for i in range(5):                  # 执行5个实例
    s = []							# 测试集
    pos = random.randint(1,6)       # 随机生成测试集的个数
    for j in range(pos):
        pr = random.randint(0,5)    # 随机产生一个括号集的序号
        while pairs[pr] in s:       # 排除相同的括号，也就是说测试集中的括号一定是不相同的！
            pr = random.randint(0,5)
        s += pairs[pr]              # 将随机产生的括号加入测试集
    print(s)
    print(check(s))

下面截取了几次的执行结果（不得不说，匹配成功的概率还是相当的低呀0.0）：


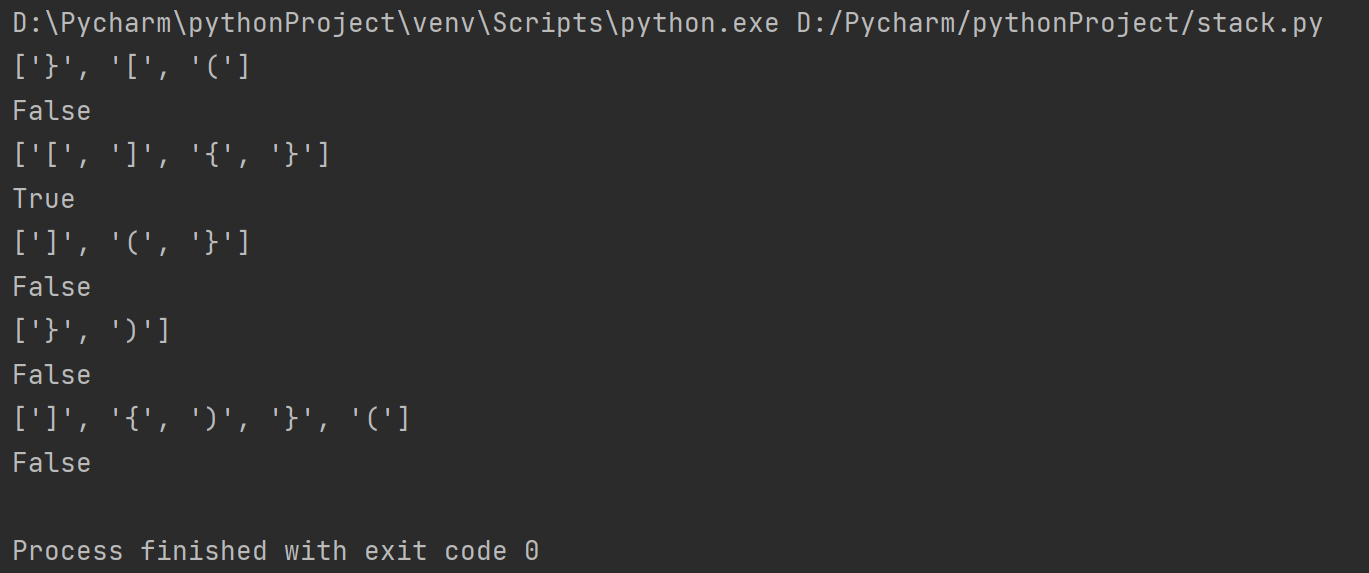
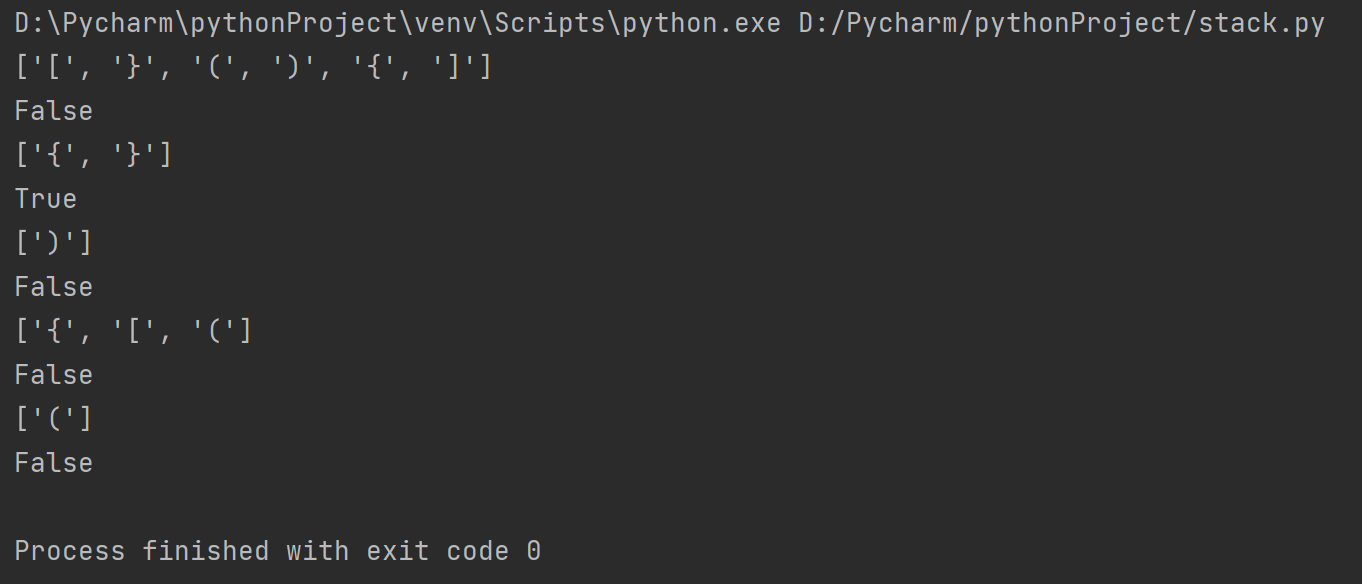
这可是我运行了好多次才有的结果

🍃 中缀表达式到后缀表达式的转换

中缀表达式：二元运算符写在两个运算对象中间的表达式。就是我们在日常生活中的数学表达式，例如“3+5*(8-4)”，上面这个表达式就是将运算符写在两个运算对象的中间。

那么由此，可以联想到后缀表达式是什么样。

后缀表达式：二元运算符写在两个运算对象后面的表达式。如果我们将上面的例子，转化为后缀表达式，那么就是“ 3 5 8 4 - * + ”。它的运算顺序就是：
1）8 4 - 也就是8 - 4，结果为4
2）5 4 * 也就是5 * 4，结果为20
3）3 20 + 也就是3 + 20，结果为23

自然而然地，也会有前缀表达式，那么前缀表达式呢就是将运算符号写在两个运算对象的前面。前缀表达式同时也被称为波兰表达式，那么后缀表达式也被称为逆波兰表达式。

为什么要将中缀表达式转换为后缀表达式？

首先，后缀表达式的出现一定是它在某些地方比中缀表达式更好。

中缀表达式的主要缺点就是：它不足以表示所有可能的运算顺序，需要通过辅助符号、约定等辅助描述机制。且中缀表达式必须引进括号的概念，规定括号里的运算先做，以便于一些特定顺序的计算。但这种处理方式非常麻烦，不适合计算机处理。

而后缀表达式中省去了括号，一个表达式只由运算对象和运算符组成，利用栈就可以实现一个后缀表达式的顺序计算。

所以类似于后缀表达式等很多不同于常规的东西，都是为了方便计算机处理而出现的。

如何利用栈进行后缀表达式的转换？

1. 首先，利用栈无非就是存储一些数据等待后面再用，所以大概的转换过程就是先顺序读取前缀表达式，遇到运算对象直接输出，遇到运算符或括号就进栈，后面再出栈。
2. 然后，基于中缀表达式中不同运算符号之间有优先级的限制，所以在进栈的时候有一定的困难。这里就需要我们人为地去规定运算符号的优先级大小。（下面数值越大的优先级越高，这里也将括号当作是运算符号）

• “(”：1
• “+”、“-”：2
• “*”、“/”：3

3. 下面以x表示顺序读取到前缀表达式中的一位，来讨论处理情况。

• 若x为运算对象：直接输出
• 若x为“(”：我们直接将左括号进栈
• 若x为“)”：这里不需要将右括号进栈，读取到右括号了就表示中缀表达式中一对括号内的读取已经结束，这时就需要挨着弹栈并输出，直到遇见左括号为止，最后再将左括号弹出。
• 若x为除括号外的其它运算符：我们需要将x入栈，但在x入栈前，我们还需要判断栈顶符号与x的优先级大小关系。若x的优先级大于等于栈顶符号，则x入栈；若x的优先级小于栈顶符号，先将栈顶元素弹出并输出后，再将x入栈（这里需要一直将x与栈顶元素比较，直到x的优先级大于栈顶符号为止，同时每次比较如果弹栈了，则还需要判断栈是否为空，为空则也直接将x入栈）
• 最后若栈内还有元素，就挨个弹出并输出

4. 下面以上面举的例子来作一个说明“3+5*(8-4)”$\to$“ 3 5 8 4 - * + ”。（红色表示读取到哪个字符了）

前缀	判断	栈内元素	后缀
3+5*(8-4)	为运算对象，直接输出		3
3+5*(8-4)	为除括号外的运算符，这里栈为空，不用与栈顶符号比较，直接进栈	+	3
3+5*(8-4)	为运算对象，直接输出	+	35
3+5*(8-4)	为除括号外的其它运算符，与栈顶符号“-”比较，x的优先级等于栈顶符号，直接进栈	+*	35
3+5*(8-4)	为左括号，直接进栈	+*(	35
3+5*(8-4)	为运算对象，直接输出	+*(	358
3+5*(8-4)	为除括号外的运算符，这里栈不为空，与栈顶符号“(”比较，“-”的优先级大于栈顶符号，直接进栈	+*(-	358
3+5*(8-4)	为运算对象，直接输出	+*(-	3584
3+5*(8-4)	为右括号，不进栈，开始挨个弹栈并输出，直到遇见左括号	+*(	3584-
3+5*(8-4)	弹栈后，栈顶符号此时为左括号，再继续将左括号弹出，不输出	+*	3584-
3+5*(8-4)	此时对前缀表达式的读取已经结束，挨个弹出栈内剩余元素并输出		3584-*+

这就是一个完整的转换过程，大家可自行写一个中缀表达式来试着转换，加深一下对这个过程的印象。下面还是用前面说的链栈来实现这个过程，上代码：

priority = {'(':1,'+':2,'-':2,'*':3,'/':3}      # 符号之间的优先级
operators = "+-*/()"                            # 符号集

def infix_to_suffix(infix):
    st = link_stack()
    suffix = []

    for x in infix:
        if x not in operators:          # 若x是运算对象
            suffix.append(x)

        elif x == '(':                  # 若x是左括号
            st.link_push(x)

        elif x == ')':                  # 若x为右括号
            while st.get_length() != 0 and st.get_top() != '(':     # 依次弹栈，直到遇到左括号为止
                suffix.append(st.link_pop())
            st.link_pop()               # 左括号出栈

        else:                           # 若x是除括号外的其它运算符
            while st.get_length() != 0 and priority[st.get_top()] >= priority[x]:        # 比较栈顶符号与x的优先级
                suffix.append(st.link_pop())                    # 若栈顶符号的优先级大于x，则应先将栈顶元素出栈并加入到后缀表达式中
            st.link_push(x)                                     # 直到栈顶符号优先级小于x，将x压栈

    while st.get_length() != 0:         # 弹出并输入栈内剩余的符号
        suffix.append(st.link_pop())

    return suffix                       # 返回后缀表达式

示例

infix = "3+5*(8-4)"
print(infix_to_suffix(infix))
infix1 = "2+4*(5+3/(9+2))/5"
print(infix_to_suffix(infix1))

执行结果如下：

PS：上面的算法中有几个缺点：

• 运算对象只能是个位数，如果是其它位数还需另作考虑
• 输入的前缀表达式一定是符合逻辑的，没有排除不符合逻辑的情况

🍃 后缀表达式的计算

学会了中缀表达式转后缀表达式后，那么后缀表达式的计算就十分简单了。

因为后缀表达式只由运算符号和运算对象组成，没有了括号，所以它整体的一个思路就是遇到运算对象直接压栈，遇到运算符后不压栈，两次弹出栈顶元素，然后对它们作一个运算，运算完成后又压栈继续运算。

需要注意的是一下两点：

• 后缀表达式是一个字符串，对它作运算我们需要进行强制类型转换成整型或浮点型
• 依次弹出两个运算对象的时候，a表示运算符号左边的运算对象，b表示运算符号右边的运算对象，在代码里需要仔细看一下

代码如下：

def calculate_suffix(suffix):
    operators = "+-*/"
    st = link_stack()

    for x in suffix:
        if x not in operators:          # 若x为运算对象，直接进栈
            st.link_push(int(x))        # 注意这里要强制转换x的类型，不然后续的计算无法进行，因为不转换的话就是字符型
            continue                    # 退出本次循环读取下一个x

        # 后面的x一定是运算符号，遇到运算符号我们就需要将栈顶元素依次取出两个
        if st.get_length() >= 2:
            b = st.link_pop()           # b是右边的运算对象
            a = st.link_pop()           # a是左边的运算对象
        else:
            raise Exception("ERROR!The length of the stack is less than 2")

        if x == "+":
            c = a + b

        elif x == "-":
            c = a - b

        elif x == "*":
            c = a * b

        else:
            c = a / b

        st.link_push(c)             # 计算后将c压栈并继续后续的计算

    return st.link_pop()            # 计算的最后栈内一定只剩一个元素

示例：

infix1 = "2+4*(5+3/(9+2))/5"
print(calculate_suffix(infix_to_suffix(infix1)))
infix2 = "3+5*(8-4)"
print(calculate_suffix(infix_to_suffix(infix2)))

执行结果如下：

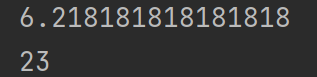
栈的学习到这里就结束了啦，如果大家有不懂的地方、或是我有不足的地方，欢迎在评论区留言！