文章目录
- 13 MCMC——马尔可夫链蒙特卡洛
- 13.1 MCMC的意义
- 13.2 简单采样方法介绍
- 13.2.1 概率分布采样
- 13.2.2 Rejection Sampling——拒绝采样
- 13.2.3 Importance Sampling——重要性采样
- 13.3 Markov Chain知识补充
- 13.3.1 Markov Chain定义
- 13.3.2 Markov Chain性质——平稳分布
- 13.3.3 Markov Chain性质——Detailed Balance
- 13.4 Metropolis Hastings方法
- 13.5 Gibbs方法
- 13.6 MCMC总结
13 MCMC——马尔可夫链蒙特卡洛
13.1 MCMC的意义
我们都知道Monte Carlo是一种常用的估计方法,我们经常用这个方法对期望进行随机估计。而Monte Carlo中的一大问题就是采样,要从一个复杂分布中采样是困难的,我们只能通过一些方法,将复杂的分布表示出来,然后进行采样。
我们从三个方面介绍一下MCMC的意义:
- 采样的动机:
- 采样本身:我们经常需要从各种概率分布中取得样本。(例如学习一张图片后生成新的图片)
- 求和或求积分(期望): E p ( x ) [ f ( x ) ] ≈ 1 N ∑ i = 1 N f ( x ( i ) ) E_{p(x)}[f(x)] \approx \frac{1}{N} \sum_{i=1}^{N} f(x^{(i)}) Ep(x)[f(x)]≈N1∑i=1Nf(x(i))
- 什么是好的样本:
- 样本趋向(集中)于高概率区域——能够凸显分布特征
- 样本之间相互独立
- 为什么会采样困难:
- 无法归一化:Partation funtion is intractable——求不出概率(归一化因子是积分形式,维度过高会无法求解)
- 维度灾难:高维的稀疏性使得直接判定的方法无法操作
13.2 简单采样方法介绍
首先简单介绍一下Monte Carlo方法:Monte Carlo Method是基于采样的随即近似方法。假如存在
N
N
N个样本
Z
(
1
)
,
…
,
Z
(
N
)
Z^{(1)}, \dots, Z^{(N)}
Z(1),…,Z(N),我们就可以通过代入样本求均值求期望:
P
(
Z
∣
X
)
→
E
Z
∣
X
[
f
(
Z
)
]
=
∫
Z
f
(
Z
)
⋅
P
(
Z
∣
X
)
d
Z
≈
1
N
∑
i
=
1
N
f
(
Z
(
i
)
)
P(Z|X) \rightarrow E_{Z|X}[f(Z)] = \int_Z f(Z) \cdot P(Z|X) d_Z \approx \frac{1}{N} \sum_{i=1}^{N} f(Z^{(i)})
P(Z∣X)→EZ∣X[f(Z)]=∫Zf(Z)⋅P(Z∣X)dZ≈N1i=1∑Nf(Z(i))
同时给出一个最基本的条件:我们认为样本
u
∽
U
(
0
,
1
)
u \backsim U(0, 1)
u∽U(0,1)的均匀分布是很好取的。
13.2.1 概率分布采样
条件:我们已知目标分布 p ( x ) p(x) p(x)的pdf,而且可以通过积分求出其cdf。
方法:因为均匀分布 u ∽ U ( 0 , 1 ) u \backsim U(0, 1) u∽U(0,1)很好取,所以我们随机取 u u u作为cdf的值,通过反函数求出样本。
缺点:大多数分布的积分、反函数求不出来,无法实现
13.2.2 Rejection Sampling——拒绝采样
条件:我们已知目标分布 p ( x ) p(x) p(x)的pdf,用 q ( x ) q(x) q(x)表示一个可以通过概率分布采样的简单的pdf,令 ∀ Z → M ⋅ q ( Z ) ≥ p ( Z ) \forall Z \rightarrow M \cdot q(Z) \geq p(Z) ∀Z→M⋅q(Z)≥p(Z)(带 M M M是因为 q q q与 p p p的面积相同,不带系数无法实现)
方法:
-
假定在样本点 Z ( i ) Z^{(i)} Z(i)时, p ( Z ( i ) ) p(Z^{(i)}) p(Z(i))的值为 l 1 l_1 l1, M ⋅ q ( Z ( i ) ) M \cdot q(Z^{(i)}) M⋅q(Z(i))的值为 l 2 l_2 l2,如图所示
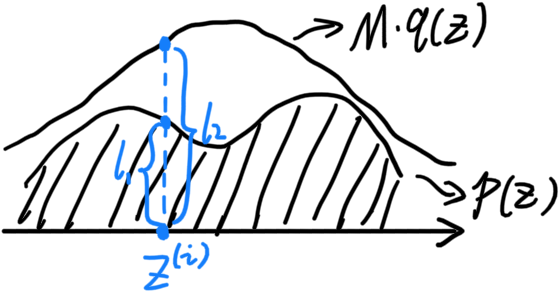
-
定义一个变量,接受率 α = l 1 l 2 \alpha = \frac{l_1}{l_2} α=l2l1,取值范围为 α ∈ [ 0 , 1 ] \alpha \in [0, 1] α∈[0,1]。
-
在对 q ( Z ) q(Z) q(Z)采样的时候,随机在均匀分布中采样: u ∽ U ( 0 , 1 ) u \backsim U(0, 1) u∽U(0,1)。若 u ≤ α u \leq \alpha u≤α则保留 Z ( i ) Z^{(i)} Z(i),反之则删除。
缺点:若 p ( Z ( i ) ) p(Z^{(i)}) p(Z(i))和 M ⋅ q ( Z ( i ) ) M \cdot q(Z^{(i)}) M⋅q(Z(i))的值相差过大,会增加运算量(可能取好多次样都保留不了几个)
13.2.3 Importance Sampling——重要性采样
原理:对取样分布进行变换:
E
p
(
Z
)
[
f
(
Z
)
]
=
∫
Z
f
(
Z
)
p
(
Z
)
d
Z
=
∫
Z
f
(
Z
)
p
(
Z
)
q
(
Z
)
⋅
q
(
Z
)
d
Z
=
E
q
(
Z
)
[
f
(
Z
)
p
(
Z
)
q
(
Z
)
]
≈
1
N
∑
i
=
1
N
[
f
(
Z
(
i
)
)
p
(
Z
(
i
)
)
q
(
Z
(
i
)
)
]
\begin{align} E_{p(Z)}[f(Z)] &= \int_Z f(Z)p(Z) {\rm d}_Z \\ &= \int_Z f(Z) \frac{p(Z)}{q(Z)} \cdot q(Z) {\rm d}_Z \\ &= E_{q(Z)} \left[ f(Z) \frac{p(Z)}{q(Z)} \right] \\ &\approx \frac{1}{N} \sum_{i=1}^N \left[ f(Z^{(i)}) \frac{p(Z^{(i)})}{q(Z^{(i)})} \right] \end{align}
Ep(Z)[f(Z)]=∫Zf(Z)p(Z)dZ=∫Zf(Z)q(Z)p(Z)⋅q(Z)dZ=Eq(Z)[f(Z)q(Z)p(Z)]≈N1i=1∑N[f(Z(i))q(Z(i))p(Z(i))]
我们将
q
(
Z
)
q(Z)
q(Z)定义为一个简单分布。通过对
q
(
Z
)
q(Z)
q(Z)进行采样,可以求出
f
(
Z
(
i
)
)
p
(
Z
(
i
)
)
q
(
Z
(
i
)
)
f(Z^{(i)}) \frac{p(Z^{(i)})}{q(Z^{(i)})}
f(Z(i))q(Z(i))p(Z(i)),我们将
p
(
Z
(
i
)
)
q
(
Z
(
i
)
)
\frac{p(Z^{(i)})}{q(Z^{(i)})}
q(Z(i))p(Z(i))称为权重,乘上倒数我们便可以得到结果:
1
N
∑
i
=
1
N
f
(
Z
(
i
)
)
(对
p
取样)
→
1
N
∑
i
=
1
N
[
f
(
Z
(
i
)
)
p
(
Z
(
i
)
)
q
(
Z
(
i
)
)
]
(对
q
取样)
\frac{1}{N} \sum_{i=1}^N f(Z^{(i)}) (对p取样) \rightarrow \frac{1}{N} \sum_{i=1}^N \left[ f(Z^{(i)}) \frac{p(Z^{(i)})}{q(Z^{(i)})} \right] (对q取样)
N1i=1∑Nf(Z(i))(对p取样)→N1i=1∑N[f(Z(i))q(Z(i))p(Z(i))](对q取样)
缺点:以来
p
p
p、
q
q
q的相似度,若相差过大,则样本位置分布的差别会很大。
推广:Sampling Importance Resampling——重采样:
- 先进行一次Importance Resampling得到 Z ( i ) Z^{(i)} Z(i)
- 通过将权重 p ( Z ( i ) ) q ( Z ( i ) ) \frac{p(Z^{(i)})}{q(Z^{(i)})} q(Z(i))p(Z(i))设置为概率重新进行采样——可以将更多的点聚集在高概率区域
13.3 Markov Chain知识补充
13.3.1 Markov Chain定义
Markov Chain定义:通过 { x t } {\lbrace x_t \rbrace} {xt}表示节点, P = [ P i j ] P=[P_{ij}] P=[Pij]表示转移矩阵(i,j用于表示节点的状态, P i j = P ( x t + 1 = j ∣ x t = i ) P_{ij} = P(x_{t+1} = j | x_t = i) Pij=P(xt+1=j∣xt=i)), π t \pi_t πt表示 t t t时刻的节点所表示的分布:

13.3.2 Markov Chain性质——平稳分布
Markov Chain性质——平稳分布:节点的分布随时间 t → ∞ t \rightarrow \infty t→∞, π t \pi_t πt将会收敛于一个固定的分布。
重定义:
- 节点为
{
x
t
}
{\lbrace x_t \rbrace}
{xt}, 状态分布为
q
(
t
)
(
x
)
q^{(t)}(x)
q(t)(x),$Q = \begin{pmatrix} Q_{11} & Q_{12} & \dots & Q_{1K} \ Q_{21} & Q_{22} & \dots & Q_{2K} \ \dots \ Q_{K1} & Q_{K2} & \dots & Q_{KK} \end{pmatrix}_{K \times K}
为转移矩阵(随机矩阵),到
为转移矩阵(随机矩阵),到
为转移矩阵(随机矩阵),到m$时刻收敛(分布不变):
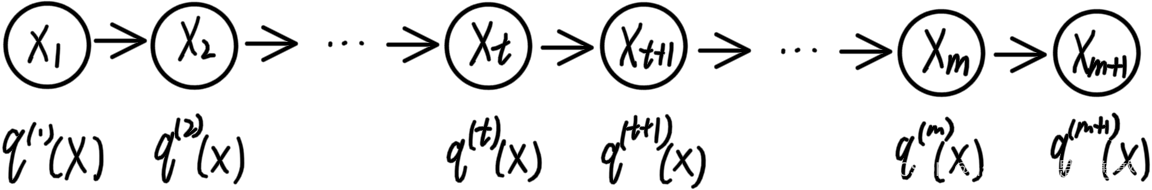
为何要引入平稳分布?
- 从结论出发,平稳分布只与转移矩阵相关(也就是说初始分布可以很简单,简单到可以取样),若平稳分布与目标分布相同的话,我们就可以通过Markov Chain的平稳分布,从简单取样到复杂取样。
收敛证明——证明对于Markov Chain, ∃ m \exists m ∃m使得 q ( m + i ) ( x ) , i ∈ N q^{(m+i)}(x), i \in N q(m+i)(x),i∈N进入平稳分布:
定义行向量: q ( t + 1 ) = ( q ( t + 1 ) ( x = 1 ) , … , q ( t + 1 ) ( x = K ) ) 1 × K q^{(t+1)} = {\left( q^{(t+1)}(x = 1), \dots , q^{(t+1)}(x = K) \right)}_{1 \times K} q(t+1)=(q(t+1)(x=1),…,q(t+1)(x=K))1×K
引入转移矩阵的定义可以得到: q ( t + 1 ) ( x = j ) = ∑ i = 1 K q ( t ) ( x = i ) ⋅ Q i j q^{(t+1)}(x=j) = \sum_{i=1}^{K} q^{(t)}(x=i) \cdot Q_{ij} q(t+1)(x=j)=∑i=1Kq(t)(x=i)⋅Qij
可以得到公式:
q ( t + 1 ) = ( ∑ i = 1 K q ( t ) ( x = i ) ⋅ Q i 1 , … , ∑ i = 1 K q ( t ) ( x = i ) ⋅ Q i K ) 1 × K = q ( t ) Q = ⋯ = q ( 1 ) Q t \begin{align} q^{(t+1)} &= {\left( \sum_{i=1}^{K} q^{(t)}(x=i) \cdot Q_{i1}, \dots , \sum_{i=1}^{K} q^{(t)}(x=i) \cdot Q_{iK} \right)}_{1 \times K} \\ &= q^{(t)}Q = \dots = q^{(1)}Q^t \end{align} q(t+1)=(i=1∑Kq(t)(x=i)⋅Qi1,…,i=1∑Kq(t)(x=i)⋅QiK)1×K=q(t)Q=⋯=q(1)Qt
引入随机矩阵的性质(Q满足随机矩阵的性质):随机矩阵的特征值的绝对值 ≤ 1 \leq 1 ≤1,所以有:
Q = A Λ A − 1 = A − 1 Λ A , Λ = d i a g ( λ 1 , … , λ k ) , ∣ λ i ∣ ≤ 1 Q = A \Lambda A^{-1} = A^{-1} \Lambda A, \quad \Lambda = diag(\lambda_1, \dots, \lambda_k), \quad |\lambda_i| \leq 1 Q=AΛA−1=A−1ΛA,Λ=diag(λ1,…,λk),∣λi∣≤1
引入性质继续分解公式可得:
q ( t + 1 ) = q ( 1 ) Q t = q ( 1 ) ( A Λ A − 1 ) t = q ( 1 ) A Λ t A − 1 \begin{align} q^{(t+1)} = q^{(1)}Q^t = q^{(1)}{(A \Lambda A^{-1})}^t = q^{(1)}{A \Lambda^t A^{-1}} \end{align} q(t+1)=q(1)Qt=q(1)(AΛA−1)t=q(1)AΛtA−1
假设目前有一个足够大的 m m m,我们可以知道:
{ q ( m + 1 ) = q ( 1 ) A Λ m A − 1 q ( m + 2 ) = q ( 1 ) A Λ m + 1 A − 1 \begin{cases} q^{(m + 1)} = q^{(1)}{A \Lambda^m A^{-1}} \\ q^{(m + 2)} = q^{(1)}{A \Lambda^{m+1} A^{-1}} \\ \end{cases} {q(m+1)=q(1)AΛmA−1q(m+2)=q(1)AΛm+1A−1
若此时 m m m足够大,不妨设其中只有 λ i = 1 \lambda_i = 1 λi=1,可得 Λ m = d i a g ( 0 , … , 1 , … , 0 ) = Λ m + 1 \Lambda^m = diag(0, \dots, 1, \dots, 0) = \Lambda^{m+1} Λm=diag(0,…,1,…,0)=Λm+1。将该公式代入上文可得
q ( m + 1 ) = q ( m + 2 ) q^{(m + 1)} = q^{(m + 2)} q(m+1)=q(m+2)
由此得证,当 t > m t>m t>m时,有 q ( m + 1 ) = q ( m + 2 ) = q ( ∞ ) q^{(m + 1)} = q^{(m + 2)} = q^{(\infty)} q(m+1)=q(m+2)=q(∞)
但这个收敛证明有一个缺点:
- 我们只证明了在足够大时会收敛,但我们不知道具体的收敛时间与条件。
13.3.3 Markov Chain性质——Detailed Balance
Detailed Balance:
- 满足以下等式(表示为双向映射):
π ( x ) ⋅ P ( x ↦ x ∗ ) = π ( x ∗ ) ⋅ P ( x ∗ ↦ x ) \pi(x) \cdot P(x \mapsto x^*) = \pi(x^*) \cdot P(x^* \mapsto x) π(x)⋅P(x↦x∗)=π(x∗)⋅P(x∗↦x)
作用:
-
Detailed Balance的条件中包含了平稳分布,因为平稳分布的性质表示为: { π k } {\lbrace \pi_k \rbrace} {πk}是 { x t } {\lbrace x_t \rbrace} {xt}的平稳分布:
π ( x ∗ ) = ∫ π ( x ) ⋅ P ( x ↦ x ∗ ) d x \pi(x^*) = \int \pi(x) \cdot P(x \mapsto x^*) {\rm d}x π(x∗)=∫π(x)⋅P(x↦x∗)dx -
要证明Detailed Balance包含平稳分布可以在两边同对 x x x积分:
∫ π ( x ) ⋅ P ( x ↦ x ∗ ) d x = ∫ π ( x ∗ ) ⋅ P ( x ∗ ↦ x ) d x = π ( x ∗ ) ∫ P ( x ∗ ↦ x ) d x = π ( x ∗ ) \begin{align} \int \pi(x) \cdot P(x \mapsto x^*) {\rm d}x &= \int \pi(x^*) \cdot P(x^* \mapsto x) {\rm d}x \\ &= \pi(x^*) \int P(x^* \mapsto x) {\rm d}x \\ &= \pi(x^*) \end{align} ∫π(x)⋅P(x↦x∗)dx=∫π(x∗)⋅P(x∗↦x)dx=π(x∗)∫P(x∗↦x)dx=π(x∗)
13.4 Metropolis Hastings方法
意义:是一种通过接受率满足Detailed Balance条件的方法。
方法:
-
我们先定义一个随机转移矩阵 Q ( Z ↦ Z ∗ ) Q(Z \mapsto Z^*) Q(Z↦Z∗),这个转移矩阵表示条件分布 Q ( Z ∗ ∣ Z ) Q(Z^*|Z) Q(Z∗∣Z),但此时:
p ( Z ) ⋅ Q ( Z ↦ Z ∗ ) ≠ p ( Z ∗ ) ⋅ Q ( Z ∗ ↦ Z ) p(Z) \cdot Q(Z \mapsto Z^*) \neq p(Z^*) \cdot Q(Z^* \mapsto Z) p(Z)⋅Q(Z↦Z∗)=p(Z∗)⋅Q(Z∗↦Z) -
定义一个接受率 α ( Z , Z ∗ ) = min ( 1 , p ( Z ∗ ) ⋅ Q ( Z ∗ ↦ Z ) p ( Z ) ⋅ Q ( Z ↦ Z ∗ ) ) \alpha(Z, Z^*) = \min(1, \frac{p(Z^*) \cdot Q(Z^* \mapsto Z)}{p(Z) \cdot Q(Z \mapsto Z^*)}) α(Z,Z∗)=min(1,p(Z)⋅Q(Z↦Z∗)p(Z∗)⋅Q(Z∗↦Z)),使得等式成立:
p ( Z ) ⋅ Q ( Z ↦ Z ∗ ) ⋅ α ( Z , Z ∗ ) = p ( Z ) ⋅ Q ( Z ↦ Z ∗ ) ⋅ min ( 1 , p ( Z ∗ ) ⋅ Q ( Z ∗ ↦ Z ) p ( Z ) ⋅ Q ( Z ↦ Z ∗ ) ) = min ( p ( Z ) ⋅ Q ( Z ↦ Z ∗ ) , p ( Z ∗ ) ⋅ Q ( Z ∗ ↦ Z ) ) = p ( Z ∗ ) ⋅ Q ( Z ∗ ↦ Z ) ⋅ min ( p ( Z ) ⋅ Q ( Z ↦ Z ∗ ) p ( Z ∗ ) ⋅ Q ( Z ∗ ↦ Z ) , 1 ) = p ( Z ∗ ) ⋅ Q ( Z ∗ ↦ Z ) ⋅ α ( Z ∗ , Z ) \begin{align} p(Z) \cdot Q(Z \mapsto Z^*) \cdot \alpha(Z, Z^*) &= p(Z) \cdot Q(Z \mapsto Z^*) \cdot \min(1, \frac{p(Z^*) \cdot Q(Z^* \mapsto Z)}{p(Z) \cdot Q(Z \mapsto Z^*)}) \\ &= \min(p(Z) \cdot Q(Z \mapsto Z^*), {p(Z^*) \cdot Q(Z^* \mapsto Z)}) \\ &= p(Z^*) \cdot Q(Z^* \mapsto Z) \cdot \min(\frac{p(Z) \cdot Q(Z \mapsto Z^*)}{p(Z^*) \cdot Q(Z^* \mapsto Z)}, 1) \\ &= p(Z^*) \cdot Q(Z^* \mapsto Z) \cdot \alpha(Z^*, Z) \\ \end{align} p(Z)⋅Q(Z↦Z∗)⋅α(Z,Z∗)=p(Z)⋅Q(Z↦Z∗)⋅min(1,p(Z)⋅Q(Z↦Z∗)p(Z∗)⋅Q(Z∗↦Z))=min(p(Z)⋅Q(Z↦Z∗),p(Z∗)⋅Q(Z∗↦Z))=p(Z∗)⋅Q(Z∗↦Z)⋅min(p(Z∗)⋅Q(Z∗↦Z)p(Z)⋅Q(Z↦Z∗),1)=p(Z∗)⋅Q(Z∗↦Z)⋅α(Z∗,Z) -
此时 Q ( Z ↦ Z ∗ ) ⋅ α ( Z , Z ∗ ) Q(Z \mapsto Z^*) \cdot \alpha(Z, Z^*) Q(Z↦Z∗)⋅α(Z,Z∗)就相当于是新的转移矩阵。
具体实现:
- 从均匀分布中取得 u ∽ U ( 0 , 1 ) u \backsim U(0, 1) u∽U(0,1)
- 从转移矩阵中进行抽样 Z ∗ ∽ Q ( Z ↦ Z ∗ ) Z^* \backsim Q(Z \mapsto Z^*) Z∗∽Q(Z↦Z∗)
- 引入接受率,对样本进行一个筛选: u ≤ α ? Z ( i ) = z ∗ : Z ( i ) = Z ( i − 1 ) u \leq \alpha ? Z^{(i)} = z^* : Z^{(i)} = Z^{(i-1)} u≤α?Z(i)=z∗:Z(i)=Z(i−1)
13.5 Gibbs方法
Gibbs实际上是特殊的MH算法,这个时候我们取 α = 1 \alpha = 1 α=1
Gibbs的思想是:
- 固定
p
(
Z
)
=
p
(
Z
1
,
Z
2
,
…
,
Z
M
)
p(Z) = p(Z_1, Z_2, \dots, Z_M)
p(Z)=p(Z1,Z2,…,ZM)中的每个维度,然后进行坐标上升。每个维度就是在条件分布中取样:
Z i ∽ p ( Z i ∣ Z − i ) Z_i \backsim p(Z_i | Z_{-i}) Zi∽p(Zi∣Z−i)
具体实现:
-
先采样出 Z 1 ( 0 ) , Z 2 ( 0 ) , … , Z M ( 0 ) Z_1^{(0)}, Z_2^{(0)}, \dots, Z_M^{(0)} Z1(0),Z2(0),…,ZM(0)
-
然后不停的上升:
{ Z 1 ( t + 1 ) = p ( Z 1 ∣ Z 2 ( t ) , … , Z M ( t ) ) Z M ( t + 1 ) = p ( Z M ∣ Z 2 ( t + 1 ) , … , Z M − 1 ( t + 1 ) ) \begin{cases} Z_1^{(t+1)} = p(Z_1| Z_2^{(t)}, \dots, Z_M^{(t)}) \\ Z_M^{(t+1)} = p(Z_M| Z_2^{(t+1)}, \dots, Z_{M-1}^{(t+1)}) \\ \end{cases} {Z1(t+1)=p(Z1∣Z2(t),…,ZM(t))ZM(t+1)=p(ZM∣Z2(t+1),…,ZM−1(t+1)) -
这样到最后将维度组合起来就是样本了
为什么Gibbs不用像MH中一样乘 α \alpha α,为什么 α = 1 \alpha = 1 α=1:
- 在Gibbs中我们假设
Q
(
Z
↦
Z
∗
)
=
P
(
Z
i
∗
∣
Z
i
)
Q(Z \mapsto Z^*) = P(Z_i^*|Z_i)
Q(Z↦Z∗)=P(Zi∗∣Zi),因为我们在求取第
i
i
i项到时候固定住了其他的项,所以有
Z
i
=
Z
i
∗
Z_i = Z_i^*
Zi=Zi∗,根据这些性质可以得到:
p ( Z ) ⋅ Q ( Z ↦ Z ∗ ) p ( Z ∗ ) ⋅ Q ( Z ∗ ↦ Z ) = p ( Z ∣ Z i ) ⋅ p ( Z i ) ⋅ Q ( Z ↦ Z ∗ ) p ( Z ∗ ∣ Z i ∗ ) ⋅ p ( Z i ∗ ) ⋅ Q ( Z ∗ ↦ Z ) = 1 \frac{p(Z) \cdot Q(Z \mapsto Z^*)}{p(Z^*) \cdot Q(Z^* \mapsto Z)} = \frac{p(Z|Z_i) \cdot p(Z_i) \cdot Q(Z \mapsto Z^*)}{p(Z^*|Z_i^*) \cdot p(Z_i^*) \cdot Q(Z^* \mapsto Z)} = 1 p(Z∗)⋅Q(Z∗↦Z)p(Z)⋅Q(Z↦Z∗)=p(Z∗∣Zi∗)⋅p(Zi∗)⋅Q(Z∗↦Z)p(Z∣Zi)⋅p(Zi)⋅Q(Z↦Z∗)=1
所以我们无需加入 α \alpha α
13.6 MCMC总结
整体思路:利用Markov Chain收敛与平稳分布的性质,设计Q使得平稳分布 ≈ \approx ≈目标分布
MCMC有的问题:
-
理论证明了收敛性,但没有给出证明结束时刻m的方法——不能简单判定相邻时刻的分布,如果提早判定了,就有可能无法测出一个较低的高峰:

-
mixing time过长: p ( x ) p(x) p(x)过于复杂/高维/高相关性
-
样本间存在一定的相关性。
将MCMC化为一张图就是: