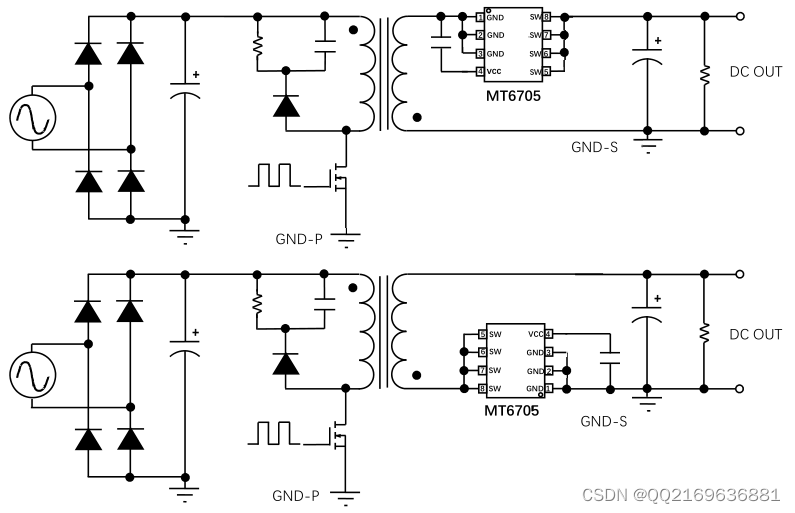
参考文献：

X. Chen, W. Wu and B. Zhang, "Robust Restoration Method for Active Distribution Networks," in IEEE Transactions on Power Systems, vol. 31, no. 5, pp. 4005-4015, Sept. 2016, doi: 10.1109/TPWRS.2015.2503426.

1.研究背景

1.1摘要

        分布式发电（DGs）不仅带来了大量估算负荷需求的不确定性，而且又加大了主动配电网络的恢复不确定性。本文提出了一种具有两阶段目标的可调鲁棒恢复优化模型，涉及不确定 DG 输出和负载需求。第一阶段为恢复停电电力生成最佳策略，第二阶段则旨在寻找最坏的波动情景。该模型被制定成了混合整数线性规划问题，使用列约束生成方法进行求解。通过这种鲁棒优化模型获得的恢复策略可以在预定义的不确定性集的所有情况下得到实现并确保良好的性能、可行性和可靠性。不确定性预算技术被用于调整模型的谨慎性，提供了谨慎性和鲁棒性的权衡。在改进的 PG&E 69-bus 系统和修改后的 246-bus 系统上进行了数值测试，以比较鲁棒优化模型和确定性复原模型，验证了这种模型的优越性。

1.2引言

        在配电网络故障发生后，服务恢复是至关重要的。故障被检测和隔离后，需要重新配置配电网络的拓扑结构，通过改变开关状态将电力恢复到停电区域。通常，确定配电网供电的恢复方案是一个多目标、组合、非线性问题，其受到多个限制条件的约束[1]。在配电网络恢复的研究方面，已经开展了大量的研究，重点关注恢复方法的效率和优化问题。在[2]–[5]中，启发式方法被用于寻找所需的解决方案。[6]比较了四种现代启发式算法的有效性，包括禁忌搜索、反应禁忌搜索、并行模拟退火和遗传算法[7]，[8]。神经网络[9]，[10]，基于知识的专家系统[11]，[12]和数学规划[13]–[15]也已应用于这个问题。

        近年来，分布式发电（DGs）在配电网络中显著增加；包括光伏和风力发电机，在主动配电网（ADNs）中是主要贡献者，但也会对稳定的电力供应构成一系列威胁[16]。需要进一步开发故障管理技术，以充分利用 ADNs。然而，分布式发电机制快速增加的渗透率，由于其波动性和间歇性，为 ADN 恢复引入了进一步的不确定性风险。事实上，完成恢复任务是一个耗时的过程，而DG的输出不是固定的，在此过程中会发生波动。尽管已经有了大量的研究致力于预测技术，但DG的输出并不容易准确预测。通过连接区域的时变负荷需求对服务恢复过程增加了进一步的不确定性。此外，由于配电网中几乎没有实时测量，因此难以获得所有负荷需求的可靠高质量估计值[17]。在现实世界中，波动的 DG 输出、时变的负荷需求以及负载误差的估计是 ADN 恢复中三个主要的不确定性因素。对于相应的不确定风险，在使用确定性模型时，恢复表现不佳可能导致这种不确定情况的出现，甚至会由于违反安全约束规定而导致某些恢复策略失败。例如，如果连接区域的负荷需求出现意外增加，原本的恢复方案可能会导致分支超负荷或电压违规。这种缺乏鲁棒性的恢复方案可能会引起额外的客户停电。因此，这种不确定性范围对传统的确定性算法在 ADN 中提出了重大挑战，需要鲁棒恢复技术来确保恢复策略的可行性和可靠性。

        一些研究[17]–[19]引入模糊方法和概率工具来建立 DG 输出和负荷需求不确定性的模型。但是，模糊数字的隶属函数是由人类经验选择的，而且需要给出随机变量的概率分布。在我们之前的工作中[20]，基于信息差决策理论提出了一种鲁棒恢复决策模型来寻找鲁棒优化策略，但是该方法中的不确定性描述过于简化。在[21]中，考虑负荷需求的不确定性，结合最优功率流的配电网重构问题。

        如上所述，ADN 恢复问题是解决最大化恢复负荷的最优恢复策略问题，同时考虑 DG 输出和负荷需求的不确定性，同时满足配电网中的操作限制。本文将此问题制定为一个两阶段自适应鲁棒优化模型，考虑 DG 输出和负荷需求的不确定性。鲁棒恢复策略意味着如果不确定的 DG 输出和负荷需求在预定的有限不确定性集内变化，它可以满足恢复期间的所有运营约束。本文的主要贡献如下。

        1）基于确定性恢复模型，我们开发了一个二阶段鲁棒性恢复优化模型（RROM），其中在ADN中的波动DG输出和负载需求被描述为预定义的不确定性集合。这些不确定性集合的边界可以从历史数据和运营商的需求中构建。在该鲁棒优化模型中，第一阶段与开关决策相关，在给定场景下生成最佳恢复策略。在第二阶段，寻找预定义不确定性集合中的最坏波动情形。这个模型产生的恢复策略的鲁棒性可以保证在不影响优化性能的情况下适用于所有不确定性场景，这已通过数值测试验证。

        2）原始的鲁棒性恢复优化模型是一个具有两阶段目标函数的混合整数二次约束规划（MIQCP）模型。为了便于求解这个模型，采用了二次约束线性化方法将MIQCP转换为混合整数线性规划（MILP）模型。

        另外，本文引入了不确定性预算策略或鲁棒性价格[22]来调整全局不确定性范围，从而控制该模型的保守性并在鲁棒性与保守性之间做出权衡。

        除本研究外，还有另一种基于信息缺口决策论（IGDT-RRDM）的鲁棒ADN恢复决策模型[20]。提出的RROM在以下两个方面优于IGDT-RRDM，这也是开发RROM的动机所在：

        （1）最优性：通过IGDT-RRDM获得的恢复策略可以保证可行性并且目标不会低于某个阈值，但它们通常不是最优的，而只是鲁棒可行的解决方案。相比之下，RROM可以在给定的恢复不确定集下始终生成鲁棒最优的解决方案，这已通过模拟结果得到了验证。

        （2）适用性：相对于IGDT-RRDM，面对ADN中的故障只能提供一个特定的帕累托最优前沿，其中每个点都与一系列参数和某种恢复策略相关联。然而，在实际应用中，如何选择IGDT-RRDM的最优参数值是一个经验性问题，没有通用的规则可供遵循。此外，每个有潜力的故障都对应着具有给定需求系数的特定帕累托最优前沿，因此在现实中完全了解所有这些前沿是相当困难的。相比之下，仅根据历史数据的剖面提供不确定性集合即可用于RROM，因此与IGDT-RRDM相比，RROM的应用要容易得多。

2.基本原理

2.1故障恢复的确定性优化模型

(1)目标函数

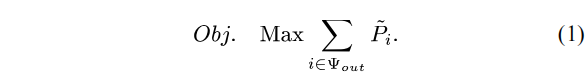
式中，为失电节点集合；为故障恢复期间节点i的实际有功负荷。模型以尽可能多地恢复失电负荷为目标，在实际中还可以考虑不同负荷的优先等级，将式中的节点负荷变为的形式，其中ωi为表征失电负荷重要性的权重因子。

(2)约束条件

 

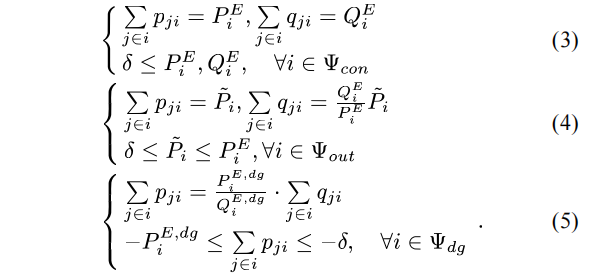
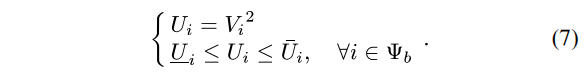
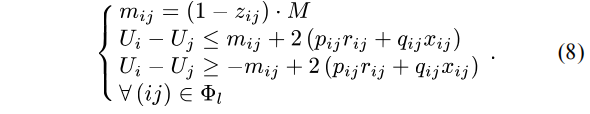
式中，zij为描述支路ij投切状态的二元名义变量，等于0表示支路断开，等于1表示支路闭合；φl表示配电系统故障隔离后所有的支路集合；nb和ns分别表示故障隔离后的节点总数和根节点数。pij和qij分别表示支路ij流过的有功和无功功率，方向为从节点i流向节点j;为支路ij的视在功率限值。ψb为故障隔离后总的节点集合；Vi为节点i的电压幅值；和分别为节点i的电压幅值平方的下限值和上限值。式(3)～式(5)依次表示带电节点、失电节点和与DG相连节点的功率平衡约束。其中，ψcon、ψout和ψdg分别表示故障隔离后带电节点集合、失电节点集合和DG节点集合；PE i和QE i分别为节点i上预期的有功无功负荷值；和分别为DG节点i上预期的分布式电源有功无功最大出力；δ为一个很小的正数，用以防止零注入孤立节点的存在；j∈i表示与节点i相连的所有其他节点。M为一个很大的正数，当zij=0即支路ij断开时，用以取消对应的潮流约束。

        此处需要注意两点。

        (1)为了简化起见，在式(4)、式(5)、式(8)中假设失电节点负荷和DG出力是以恒功率因数变化的；

        (2)在以上三个公式所表示的功率平衡约束中，忽略了网络功率损耗，即所有表示网损的二次项均被去掉，在后面的潮流方程约束中也是如此。尽管这样的处理会在潮流计算上引起偏差，但对于恢复策略的制定一般没有影响。

        为了便于对偶化处理，需要对恢复控制模型进行线性化，而原模型的表达式均为线性形式除了二次约束条件式(6)。对此，可以采用如图1所示的圆约束线性化的方法，用多个旋转正方形约束对二次圆约束进行逼近。

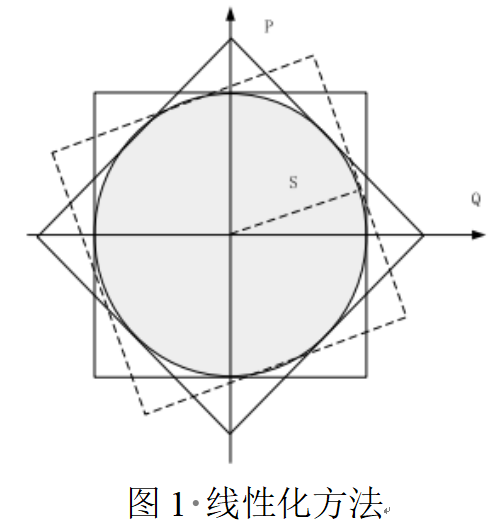
        可以看出，使用的正方形约束越多，对二次约束逼近的精确度越高。在一般的工程应用中，使用两个呈45°夹角的正方形约束就足够精确了。因此，将用线性形式的式(13)替代式(6),即线路容量约束变为如下所示。 

 

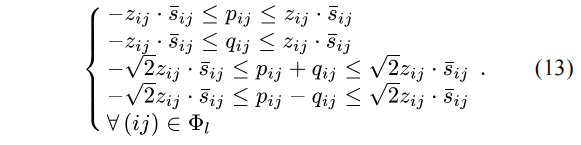
        最终，恢复控制优化模型转变为了一个混合整数线性规划MILP的形式。所建立的网络重构MISOCP模型和恢复控制的MILP模型都具有优良的求解性能，利用现有的Cplex、Gurobi、Mosek等算法包可直接获得较好的求解

2.2故障恢复的鲁棒优化模型(RROM)

        基于故障恢复的确定性优化模型，我们考虑了故障恢复时DG输出功率以及负荷需求的不确定性，并将其描述为预定义的多面体不确定度集Π：

 

 

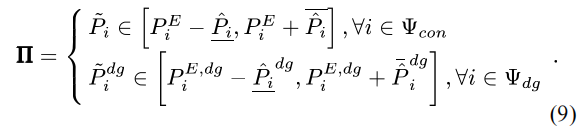
式中，Ω为恢复策略向量z(对应于线路投切决策{zij})的凸集可行域。向量p表示不确定有功负荷值与不确定DG有功出力值，隶属于不确定区间Π。在式(11)中，假设带电区域负荷是以恒功率因数波动的。

        RROM的目标函数为一个最大化最小最大问题的二阶段形式；在第一阶段以恢复策略向量z为决策变量，生成最大化恢复电量的恢复决策；在第二阶段，于给定的不确定区间Π中搜索出影响负荷恢复的最恶劣波动场景；而整个模型就是在一种最恶劣情况下制定出相应最优的决策方案。因此，由RROM生成的恢复策略将具有不确定因素的“免疫性”,即对给定不确定区间内的所有波动场景均具有可行性和鲁棒性。

        然而，由于RROM考虑的是整个给定不确定性区间内的最恶劣波动场景，可能导致恢复策略过于保守而缺乏优化性，这也是鲁棒方法为保证鲁棒性而需要付出的潜在代价。对此，采用不确定性预算技术来控制鲁棒模型的保守性。通过引入波动因子作为辅助变量，可将不确定性区间Π表示为下列形式：

式中，节点i对应的波动因子为属于[0,1]之间的正则化变量，用来描述不确定量向上或向下偏离预期值的程度。当波动因子的取值组合被确定时，实际的负荷需求和分布式电源出力也随之被确定。特别地，若波动因子的取值组合为,则表示不确定量取原给定区间的上限值；若取值组合为,则表示不确定量取区间的下限值。

        此外，需要添加额外的约束条件(16)来实现不确定性预算控制。式中的参数N为不确定性预算值，用来限制波动因子总和的大小，由此控制不确定量的全局波动范围。

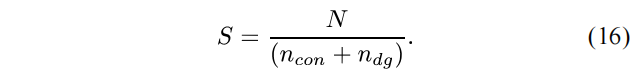
        当配电系统完成故障隔离后，波动节点数目(ncon+ndg)就成了已知参数。可以通过从0到1调整鲁棒强度S的大小，来改变实际的不确定性区间范围，从而控制鲁棒模型的整体保守性，以实现模型保守性可调的功能。特别地，当S取0时，RROM就完全等价于原本的确定性模型DROM;当S取1时，RROM便是考虑整个给定不确定性区间内的最恶劣场景。在实际应用中，鲁棒强度S的大小可根据恢复需求和目的进行选择，并作为已知参数添加到鲁棒模型中进行优化计算。到此鲁棒模型建立完毕，从数学形式上来看，RROM是一个两阶段的混合整数线性规划问题。 

2.3两阶段鲁棒模型的求解

        在本小节中，将给出两阶段鲁棒恢复控制优化模型RROM的求解算法。为了使表述更清晰，将RROM用如下所示的矩阵形式进行描述：

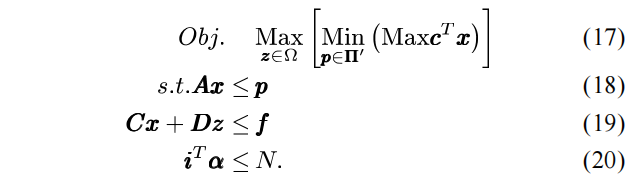
        在模型最内层的优化中，以潮流变量(pij,qij,Ui)作为决策向量x。式(18)表示所有与投切策略z相关的约束条件；其余的约束条件，包括DG节点和带电区域节点的功率平衡约束，均用式(19)表示；此处将功率平衡等式改用统一的不等式形式进行描述，使得表达形式更为紧凑简单。式(20)为不确定性预算约束，其中的α为波动因子向量，i为元素均为1的单位列向量，维数与α相同。从式(20)可以看出，特定的一组α的取值，就代表着故障恢复中某一个特定的波动场景。

        RROM是一个两阶段的优化问题，可采用列约束生成法(column and constraint generation method, C&CG)进行求解(C&CG算法详细步骤和原理可以参考我之前的博客：https://blog.csdn.net/weixin_44209907/article/details/130720240)。根据原问题中目标函数两个阶段的不同任务，将RROM分解为主问题(master problem)和子问题。

        1)主问题MP(Master Problem)

        鲁棒恢复控制模型的主问题对应着RROM中的第一阶段决策，具体形式如下所示：

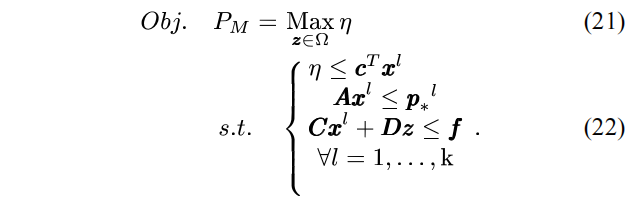        主问题是在满足运行约束的条件下，产生最优的投切策略以最大化恢复失电负荷量。在式(21)中，不确定负荷和不确定DG出力向量p被已知的向量p*替代，意味着主问题中的波动场景是给定已知的。原本不确定性集合中所有可能的波动情况，用带有上标l的部分枚举场景替代，故主问题的最优值PM为原目标函数式(17)的一个上界值。从数学形式上来看，主问题是一个单一优化目标形式的混合整数线性规划问题。 

        2)子问题SP(SubProblem)

        该子问题对应于表达式（17）中的min-max问题，如下所示：

 

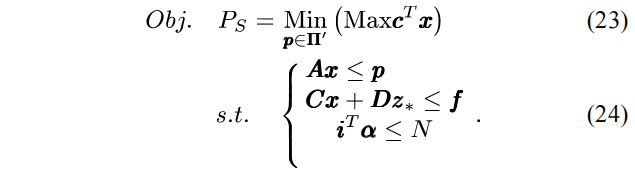
        给定恢复策略z*,子问题进行最恶劣波动场景p的搜索，并求出相应的复电量PS。由于PS是某一给定恢复策略下最恶劣场景的恢复负荷量，因此它为原目标函数式(17)提供一个下界值。子问题中的目标函数为最小最大两层优化的形式，不易于数值求解。对此，可通过引入拉格朗日乘子λ对子问题进行对偶化，将其转变为单一优化目标形式的对偶子问题，如下所示。由于子问题为混合整数线性形式，具有强对偶性，故该变形是严格等价的。  

 

 

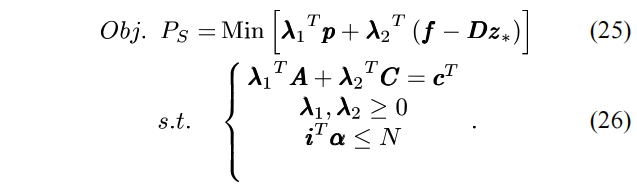
        3)求解两阶段鲁棒优化问题的C&CG算法

        将RROM分解为主问题和子问题，并相应处理完后，需要执行列约束生成法的迭代过程来进行求解，具体的迭代算法如下。

        由于主问题和对偶子问题均为混合整数线性规划的形式，可以用各种商业优化求解器如IBM ILOG CPLEX进行有效求解。

3.编程思路分析

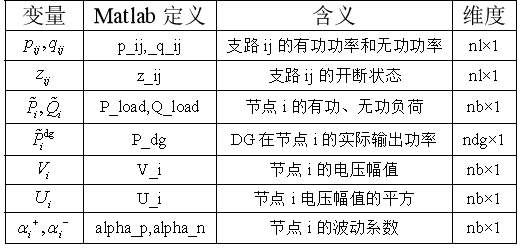
3.1参数和变量定义

 表1 相关参数

 表2 决策变量

3.2编程思路与难点

        根据对文献内容的解读，可以设计下面的编程思路：

步骤1：输入所需数据

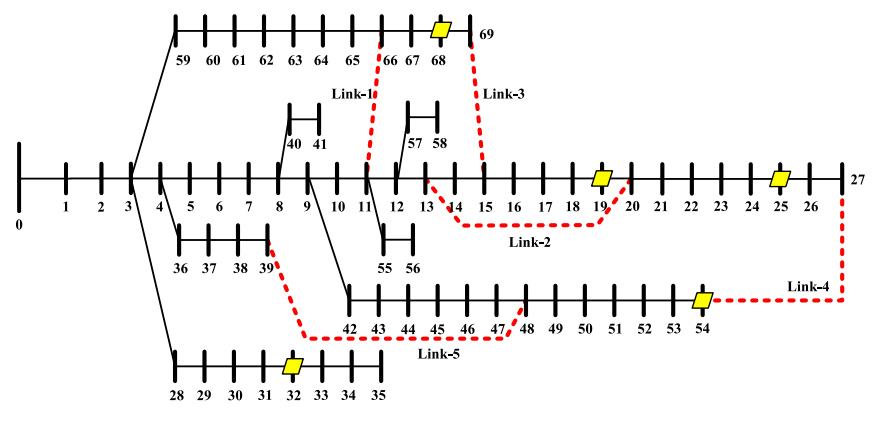
        原文献中涉及了PG&E69节点及两个123节点组成的246节点配电网，其中原文中提到PG&E69节点配电网的数据来源于1989年的文献《Optimal capacitor placement on radial distribution systems》。这部分主要有以下几个难点：

        1.PG&E69节点测试系统的数据问题。

        其实我从一开始对这个配电网就有很多疑问，在国内外各种文献、数据库、网络资料中，可以找到号称PG&E69的很多种不同版本(我自己见过至少5种，流传最广的应该是Matpower中的case69.m文件版本以及那个excel表格版本)，而且仔细看会发现，这些不同版本的数据好像只是节点编号不一样。后面我仔细看了原文献，发现图中节点编号并不是严格按照1-69的顺序，不仅有2e,27e这类字母和数字结合编号，也有88,89这类超出69的节点编号，如图2所示。所以不同的数据版本应该是把节点从1-69重新编号时，顺序不一样导致的。我在代码文件中就以Matpower中case69提供的数据为准。

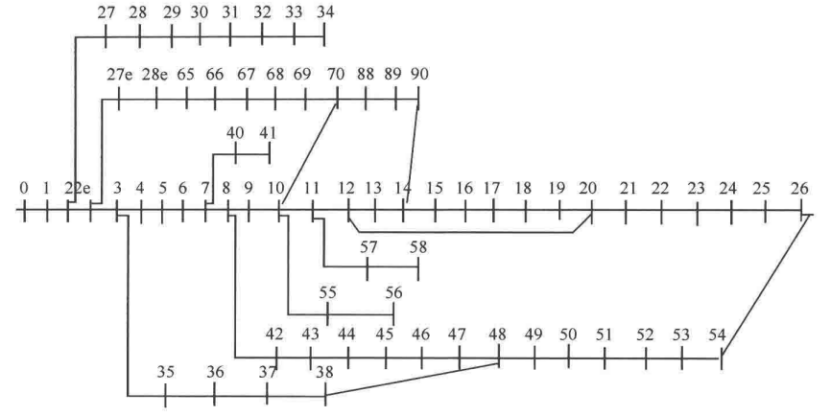
图2 PG&E69节点系统拓扑图 

        2.关于故障隔离后带电节点集合ψcon以及失电节点集合ψout的确定方法。

        文中把故障隔离后带电节点以及失电节点的功率平衡公式分开来写，但是并没有提到这两个集合是怎么确定的。我在代码中使用的是供电路径法：求出主电源到每个节点的供电路径，假设节点i到主电源的供电路径为Li，当节点i的供电路径Li中有支路故障时，就认为该节点在故障恢复过程中是失电节点。

步骤2：定义决策变量

        这一步比较简单，按照表2，初始化决策变量即可。要注意的是每个决策变量的维度以及类型(sdpvar还是binvar)不要出错。

        节点波动系数在式(14)、(15)只提到是0到1之间的连续变量，但实际上后文公式(28)又说明了是0-1变量，定义的时候不要出错。

步骤3：定义目标函数和约束条件

        这部分的问题和难点如下：

        1.关于功率平衡方程有一些不理解的地方。

        ①在功率平衡方程中没有标明主供电源节点。原文献给的潮流方程中，没有涉及主电源节点的输出功率，只有含DG节点的输出功率表达式。但是文中提供的算例，只靠DG供电显然无法满足所有负荷的需求，需要加上主供电源节点的功率平衡约束，或者把主供电源和DG节点放在一起考虑。

        ②关于ψdg集合中节点的功率表达式。原文中ψcon集合功率平衡约束中并没有涉及DG输出功率，所以提到的负荷PE i和QE i应该是指净负荷(也就是节点的负荷减去节点DG的输出功率)，但是从修改后的不确定集合Π’中(式14、15)看，ψdg和ψcon两个集合又好像是并列关系，让人感到非常迷惑。另外，从文中的表述来看，是可以实现DG给失电节点供电的，也就是形成供电孤岛。这样来看的话ψdg、ψcon以及ψout三个集合应该是并列的关系，也就是三个集合的并集才等于所有节点的集合。这么想到话原文中的潮流约束肯定是不太正确的，所以代码中潮流方程就是按照我自己的逻辑写的，没用到原文中提到的公式。我也采用的是线性潮流，差别应该不会很大。

        2.在这里强调一点，配电网最优潮流最容易踩坑的地方就是标幺值转换上。之前有朋友拿自己写的代码问我，说感觉公式模型都是按照参考文献打的，但一用求解器就是“Infeasible problem”，拿给我一看，参数中有的数值用的是实际值，有的数值用的是标幺值，非常混乱，我把参数统一修改为标幺值就可以正常运行了。

        参考原文中所给的公式，代码中所用到的确定性优化问题如下：

        目标函数：

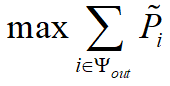
         约束条件：

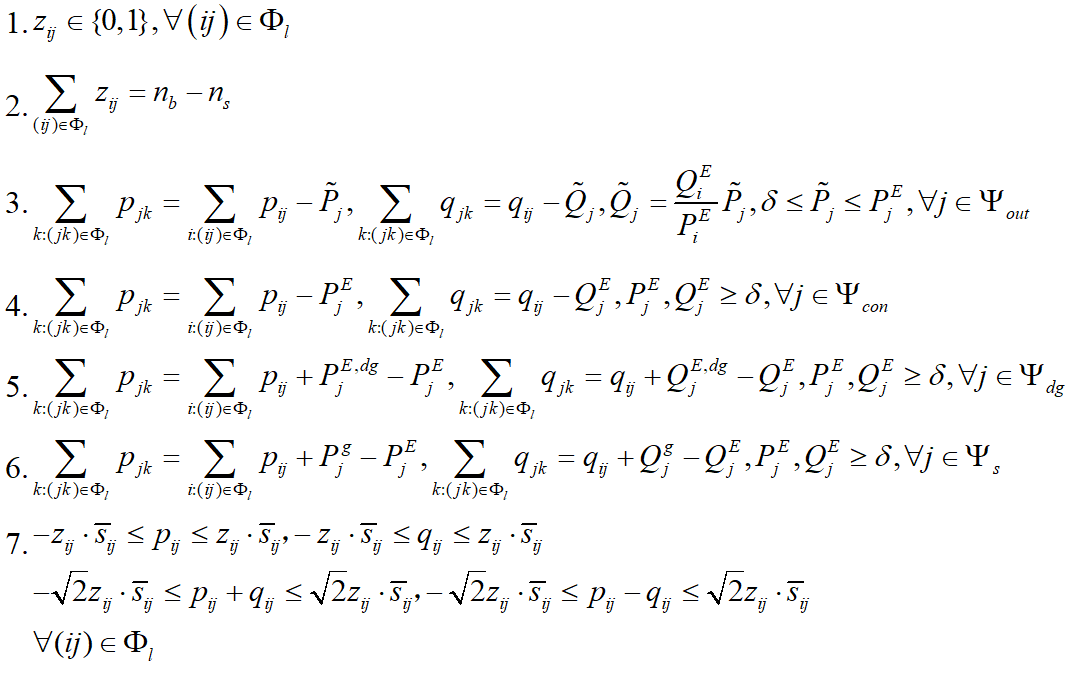
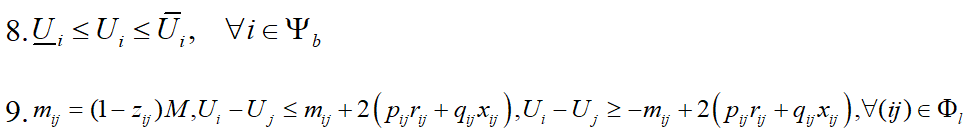
步骤4：求解确定性优化问题

        确保决策变量的定义、目标函数及约束条件的书写无误之后，就可以求解确定性优化问题。

        确定性优化问题可以正常求解，才可以进一步求解鲁棒优化问题。

步骤5：求解两阶段鲁棒优化的主问题

        关于目标函数和决策变量。原文献对目标函数(17)的解释中提到，变量x包括pij,qij和Ui，但是目标函数是关于失电节点的恢复负荷最大化，所以需要通过潮流等式转换一下表达方式，原文中这一块说的比较模糊，需要靠自己理解。我采用的方式是在变量x中加入，假设只有DG存在不确定性，而负荷是确定的，以避免繁琐的变量转换，同时约束条件(18)也可以改写成Ax≤b的形式。

        确定性优化问题能正常求解后，就可以加入不确定变量，调试两阶段鲁棒优化问题的主问题是否能正常求解。为了便于两阶段鲁棒优化编程求解，需要把所有的系数写成紧凑的矩阵形式，所有的决策变量写成向量形式，转换过程如下：

        决策变量的转换：

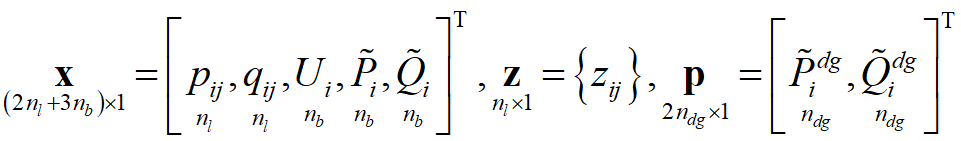
        以PGE69节点系统为例，决策变量x是一个(2×73+3×69)×1的变量，也就是353维的列向量，决策变量z是73维的列向量，不确定变量p是10维的列向量。

        目标函数的转换：

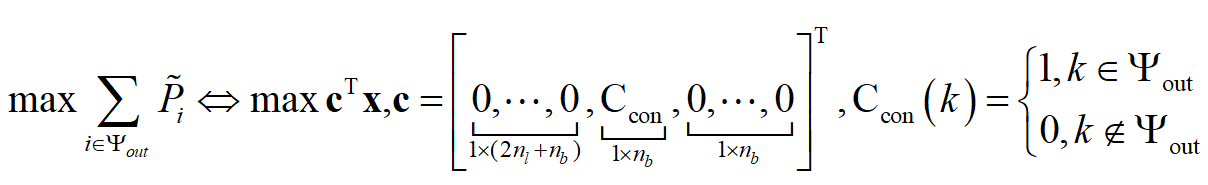        约束条件的转换相当复杂，如果直接从原始的约束条件改成矩阵形式得花费不少脑细胞。这时候就可以巧妙地利用yalmip工具箱中的’see’命令，下面是一个例子：

 

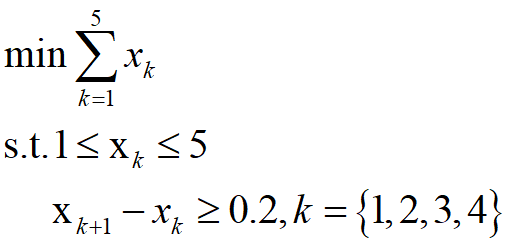
        使用yalmip求解的代码为： 

x = sdpvar(1,5);
Constraints = [1 <= x , x <= 5];
for k = 1:4
    Constraints = [Constraints , x(k+1) - x(k) >= 0.2];
end
objective = sum(x);
optimize(Constraints,objective);

         最优解为：

 

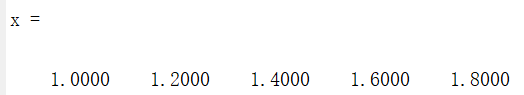
        其中约束条件Constraints是一个6×1的lmi类型变量，采用’see’函数可以求出每个约束条件对应的系数矩阵：

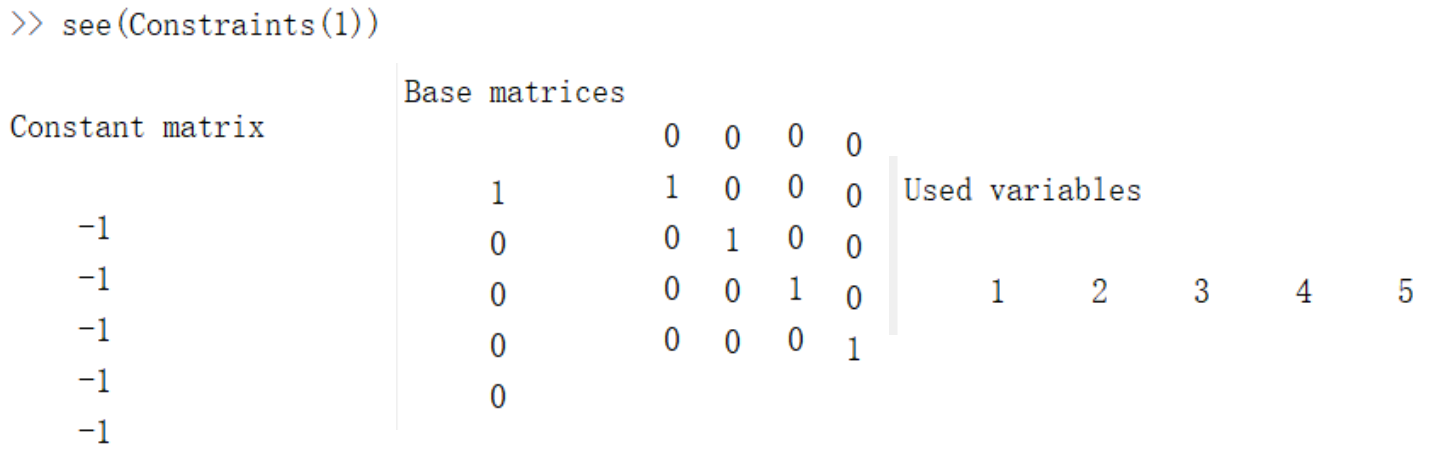
        这样就可以把存储在Constraints中的约束条件转为Ax<b的矩阵形式，其中Constant matrix代表的就是每个约束条件对应的b，Base matrices是每个约束条件对应的A，Used variables是每个约束条件用到的变量编号，这样就可以很容易把上面的约束条件转为矩阵形式：

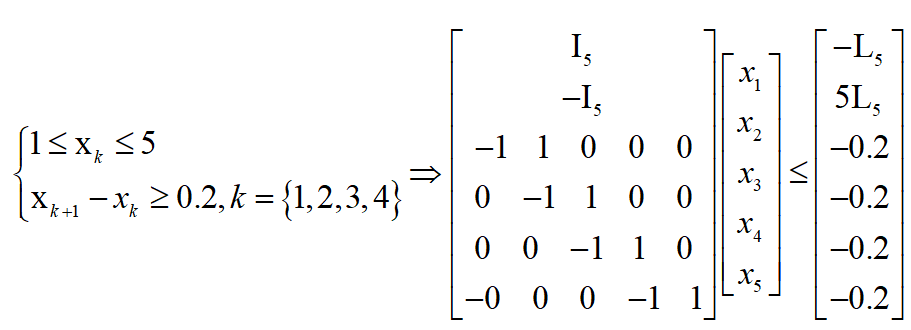
        其中I5表示5阶单位矩阵，L5表示5×1的全为1矩阵。

        采用相同的方法，可以将原文献中的问题转为易于处理的矩阵形式，此处不再赘述。

        另外，文中把优化问题写成紧凑的矩阵形式，是为了便于子问题进行对偶变换。如果使用KKT条件的话，不需要复杂的矩阵变换，就可以将子问题的双层优化形式转为单层优化。因此为了方便起见，我在代码中没有将优化问题转换为矩阵形式，而是采用直接求解的方式。

        在matlab编写主问题的函数时，输入参数应包括当前迭代次数(用于确定新增加的变量xl和相应的约束条件)和不确定变量p的取值，输出参数包括决策变量zij和LB。

步骤6：求解两阶段鲁棒优化的子问题

        子问题是一个min-max的双层优化问题，文中用到对偶变换转为单层优化问题，具有一定的难度(求优化问题的系数矩阵和对偶转换比较困难)，也比较容易出错。实际编程的时候，可以直接用KKT条件将双层优化问题转为单层优化问题(强对偶成立，KKT条件就是优化问题取最优的充要条件)，如果不太明白双层优化或KKT条件是啥，可以看看我之前的博客(双层优化入门系列)。

        我在代码中是采用yalmip编程的，直接用yalmip工具箱中的KKT函数就可以解出内层max问题的KKT条件，非常方便。这样就可以将min-max的双层优化子问题转为单层优化问题，并使用求解器求解。

        在matlab编写子问题的函数时，输入参数应包括0-1决策变量zij的取值和不确定变量p的取值，输出参数包括不确定变量p和UB。

步骤7：采用C&CG算法迭代求两阶段鲁棒优化问题最优解

        有关算法的基本原理可以看我之前的博客。

        我在刚开始学习两阶段鲁棒优化也在网上购买过一些资料。但是大多在原理上存在问题，C&CG（列与约束生成算法）就是在迭代过程中不断向主问题添加新的约束条件和决策变量，但很多代码里只添加了约束条件而没有添加决策变量，从原理上来看就是错误的。我最开始也是按照这些网传代码的做法编程，但之后还是对照曾波老师的原始文献，重新学习了C&CG算法，才发现之前的做法都是错的，只增加约束条件而不增加决策变量的方式，其实有点像Benders对偶割平面法。

步骤8：输出计算结果

        原文还涉及到作者之前的写的文章中的方法IGDT-RRDM(robust restoration optimization model based on information gap decision theory)，暂时还没有复现。

4.完整Matlab代码

        所有的数据文件以及完整的matlab代码可以从这个链接获取：

🍞正在为您运送作品详情

5.运行结果分析

5.1表4

        运行main_DROM69.m文件，分别输入1和2，得到初始场景及最恶劣场景下支路13-14断开时确定性故障恢复问题的结果：

        运行main_RROM69.m文件，得到初始场景及最恶劣场景下支路13-14断开时两阶段鲁棒故障恢复问题的结果：

 

5.2图3和表4

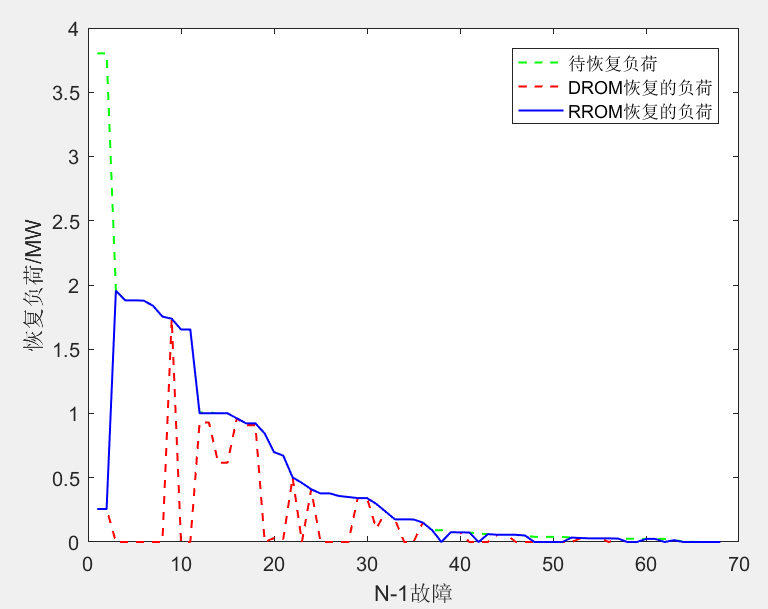
        运行N_1_fault_scan.m文件，得到所有N-1故障下，最恶劣的场景中可恢复的负荷曲线、DROM恢复的负荷曲线以及RROM恢复的负荷曲线。(由于需要逐个扫描故障，该程序运行时间较长，我的电脑运行时间为40分钟，供参考)

 

5.3表5

        原文中蒙特卡洛模拟的次数是2000次，但我估计了一下运行速度，完成5种故障的2000次仿真，我的电脑需要100个小时左右。为了快速看到效果，我在代码中把模拟次数降低为20次，如果想实现2000次仿真的效果，在代码中修改仿真次数即可。

        运行monte_carlo.m文件，得到蒙特卡洛模拟下，两种方法的恢复性能。

        我们可以分析一下该结果。当支路15-16故障时，故障隔离后节点16-27失去供电。但是无论DG输出功率多少，通过配电网重构，利用联络线15-69或13-20或27-54恢复这些节点的供电，所以确定性优化和两阶段鲁棒优化的结果应该是一样的。其他3种故障也是同理。所以两种方法的结果应该是一样的，原文献中不知道为什么会出现不同的结果。

        而当支路20-21故障时，故障隔离后节点21-27失去供电。只能利用联络线27-54恢复供电，但节点50的负荷过大，供电半径太大会导致节点电压越限，因此DROM会出现恢复失败的情况，而RROM考虑到最恶劣场景，所以可以恢复负荷。