首先给出数学上的知识。
1.
2.
3.
其次给出PINN最基础的理解与应用说明。
1.PINN中的MLP多层感知机的作用?
答:目的是用来拟合出我们需要的那个 常微分方程,即函数逼近器。
2.PINN中物理信息的作用?
答:用于约束MLP反向传播梯度下降求解时的解空间。所以PINN只需要更少的数据就能完成任务。
拟合sin(x)时的边界条件。
1.
2.参照上面的数学式子。
PINN最容易入手的就是根据各种边界条件设计出不同的损失函数(loss function),让MLP最小化这些损失函数的和或者加权和。
下面是代码部分:
import torch import torch.nn as nn import numpy as np import matplotlib.pyplot as plt from torch import autograd class Net(nn.Module): def __init__(self, NN): # NN决定全连接层的神经元个数,对拟合快慢直接相关 super(Net, self).__init__() self.input_layer = nn.Linear(1, NN) self.hidden_layer = nn.Linear(NN,int(NN/2)) self.output_layer = nn.Linear(int(NN/2), 1) def forward(self, x): out = torch.tanh(self.input_layer(x)) out = torch.tanh(self.hidden_layer(out)) out_final = self.output_layer(out) return out_final net=Net(6) # 6个 mse_cost_function = torch.nn.MSELoss(reduction='mean') # 最小化L2范数 optimizer = torch.optim.Adam(net.parameters(),lr=1e-4) # 优化器 def ode_01(x,net): # 使用神经网络net(x)作为偏微分方程的函数逼近器,每经过一次梯度更新就对对net(x)求一次导,代码中net(x)需要去逼近sin(x) y=net(x) # 求net(x)在0点的导数 y_x = autograd.grad(y, x,grad_outputs=torch.ones_like(net(x)),create_graph=True)[0] # sin**2 + cos**2 - 1 = 0 return torch.pow(y, 2)+torch.pow(y_x, 2)-1 # 动态图 plt.ion() # 总的迭代次数 iterations=20000 # 粒度N_,决定将区间分为多少个间隔 N_ = 200 for epoch in range(iterations): optimizer.zero_grad() # 梯度归0 # sin(0) - 0 = 0 x_0 = torch.zeros(N_, 1) y_0 = net(x_0) mse_i = mse_cost_function(y_0, torch.zeros(N_, 1)) # sin(-3.14) - 0 = 0 x_n314= torch.full((N_,1), -3.14) y_n = net(x_n314) mse_n = mse_cost_function(y_n, torch.zeros(N_, 1)) # sin(3.14) - 0 = 0 x_p314 = torch.full((N_,1), 3.14) y_p = net(x_p314) mse_p = mse_cost_function(y_p, torch.zeros(N_, 1)) # 输入数据,-pi到+pi之间 x_in = np.random.uniform(low=-3.14, high=3.14, size=(N_, 1)) # 将输入数据转为torch张量 pt_x_in = autograd.Variable(torch.from_numpy(x_in).float(), requires_grad=True) # pt_y_colection 是 sin**2 + cos**2 - 1 = 0 的值 pt_y_colection=ode_01(pt_x_in,net) # 全是0 pt_all_zeros= autograd.Variable(torch.from_numpy(np.zeros((N_,1))).float(), requires_grad=False) # sin**2 + cos**2 - 1 与 0 之间的误差 mse_f=mse_cost_function(pt_y_colection, pt_all_zeros) # 各种误差之和 loss = mse_i + mse_f +mse_n + mse_p # 反向传播 loss.backward() # 优化下一步 optimizer.step() if epoch%1000==0: y = torch.sin(pt_x_in) # y 真实值 y_train0 = net(pt_x_in) # y 预测值,只用于画图,不输入模型,注意区分本代码的PINN与使用MLP进行有监督回归的差别 print(epoch, "Traning Loss:", loss.data) plt.cla() plt.scatter(pt_x_in.detach().numpy(), y.detach().numpy()) plt.scatter(pt_x_in.detach().numpy(), y_train0.detach().numpy(),c='red') plt.pause(0.1)
结果展示部分:
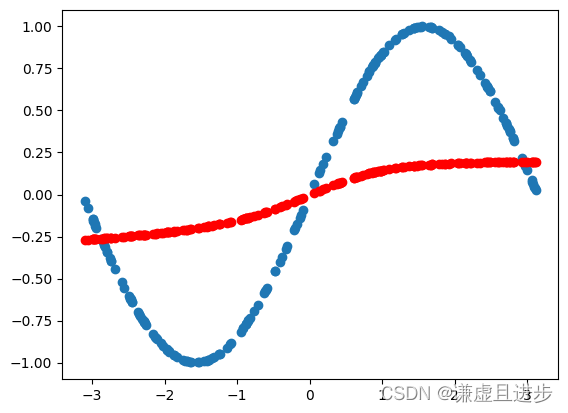
1000次迭代:
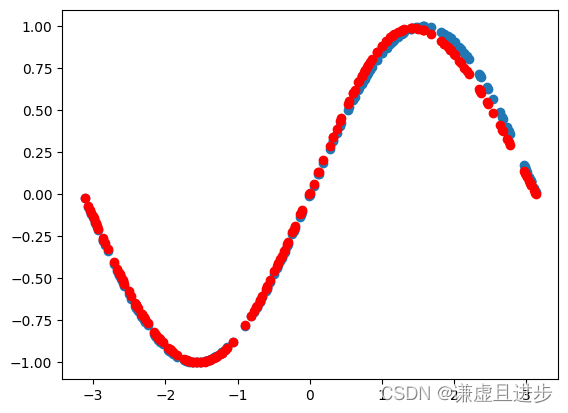
3000次迭代:
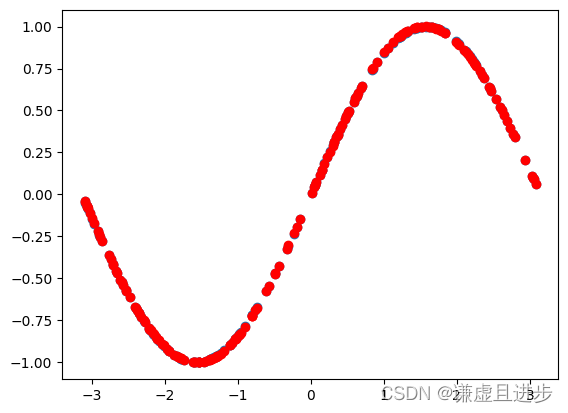
8000次迭代:
20000次迭代:
可以看到,20000次迭代之后,MLP完美逼近了sin(x)。而且不是通过有监督回归得到的。参考博客如下:PINN学习与实验(一)__刘文凯_的博客-CSDN博客。