Python集合学习笔记

news2025/1/13 13:37:11

'''
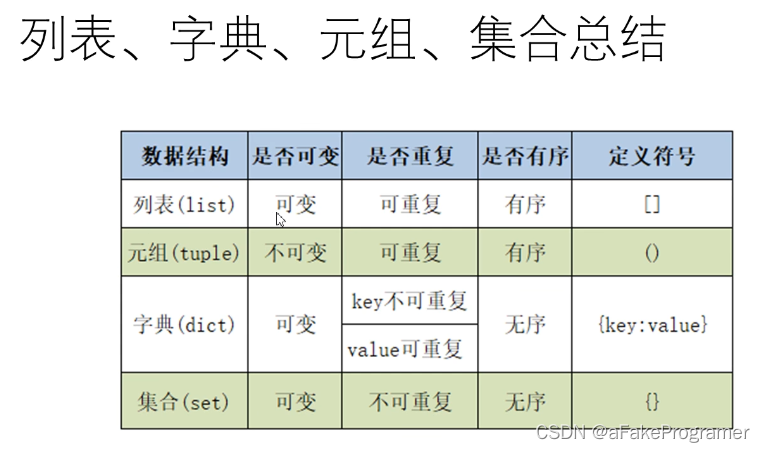
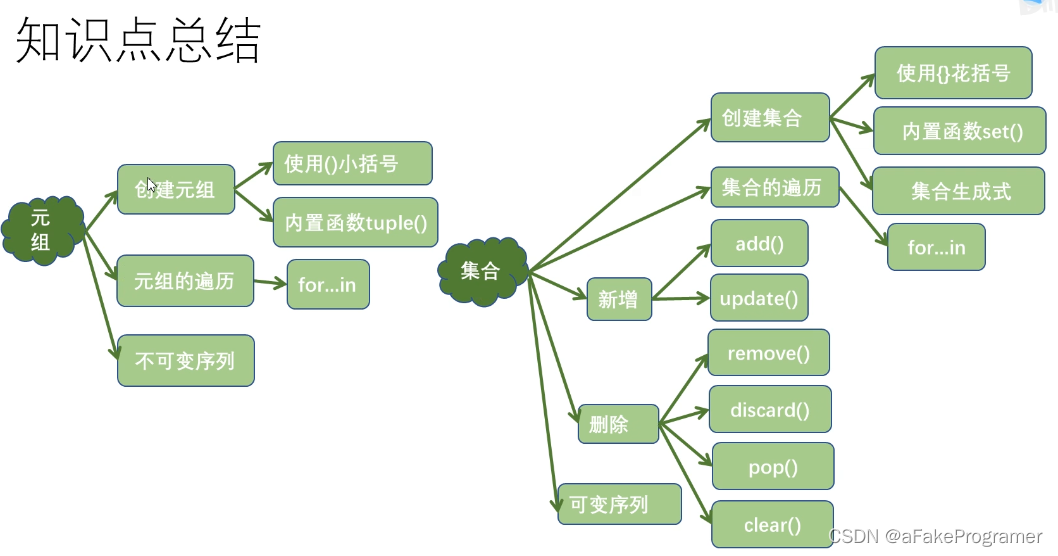
列表、字典、集合都是可变类型的序列.
集合是没有value的字典
'''
s = {2, 3, 4, 5, 5, 5, 5, 6, 7, 7}
print(s)  # {2, 3, 4, 5, 6, 7} 集合中没有相同的元素，元素不能重复

print('===================')
s1 = set(range(6))
print(s1)  # {0, 1, 2, 3, 4, 5}
lis = [2, 5, 8, 5, 8, 4, 9]
s2 = set(lis)
print(s2, type(s2))  # {2, 4, 5, 8, 9} <class 'set'>

s3 = set((11, 2, 3, 4, 51, 51, 61, 61, 71, 71, 56))  # 通过元组转
print(s3, type(s3))  # {2, 3, 4, 71, 11, 51, 56, 61}  <class 'set'> 集合中的元素是无序的，无重复元素
s4 = set('ppppythoooonnn')
print(s4, type(s4))  # {'t', 'y', 'o', 'p', 'h', 'n'} <class 'set'>

s5 = set({0, 11, 21, 3, 3, 3, 3, 4, 4, 4, 4, 5})
print(s5, type(s5))  # {0, 3, 4, 5, 21, 11} <class 'set'>

s6 = {}
print(type(s6))#<class 'dict'>
s7 = set()
print(type(s7))#<class 'set'>

输出：

{2, 3, 4, 5, 6, 7}
===================
{0, 1, 2, 3, 4, 5}
{2, 4, 5, 8, 9} <class 'set'>
{2, 3, 4, 71, 11, 51, 56, 61} <class 'set'>
{'o', 'p', 'n', 't', 'h', 'y'} <class 'set'>
{0, 3, 4, 5, 21, 11} <class 'set'>
<class 'dict'>
<class 'set'>


print('====in  not in=======')
s2 = {10, 20, 30, 40, 405}
print(10 in s2)
print(100 in s2)
print(100 not in s2)

print('====集合元素的添加操作=======')
s2.add(88)
print(s2, len(s2))
s2.update({200, 400, 300})  # 一次添加多个元素
print(s2, len(s2))
s2.update([210, 410, 310])
print(s2, len(s2))
s2.update((220, 440, 330))
print(s2, len(s2))

print('====集合元素的删除操作=======')
s2.remove(400)
print(s2, len(s2))
# s2.remove(500)# remove没有的集合元素，会报错 KeyError: 500
s2.discard(500)  # discard 有500 就从集合中删除，没有就不操作
print(s2, len(s2))


print('====集合元素删除=======')
#s2.pop(200)#不能添加参数 TypeError: pop() takes no arguments (1 given)
print(s2, len(s2))
s2.pop()  # 删除任意一个元素
print(s2, len(s2))
s2.clear()
print(s2, len(s2))

输出：
====in not in=======
True
False
True
====集合元素的添加操作=======
{40, 10, 20, 405, 88, 30} 6
{40, 200, 10, 300, 400, 20, 405, 88, 30} 9
{40, 200, 10, 300, 400, 210, 20, 405, 310, 88, 410, 30} 12
{440, 40, 200, 10, 330, 300, 400, 210, 20, 405, 310, 88, 410, 220, 30} 15
====集合元素的删除操作=======
{440, 40, 200, 10, 330, 300, 210, 20, 405, 310, 88, 410, 220, 30} 14
{440, 40, 200, 10, 330, 300, 210, 20, 405, 310, 88, 410, 220, 30} 14
====集合元素删除=======
{440, 40, 200, 10, 330, 300, 210, 20, 405, 310, 88, 410, 220, 30} 14
{40, 200, 10, 330, 300, 210, 20, 405, 310, 88, 410, 220, 30} 13
set() 0

Process finished with exit code 0


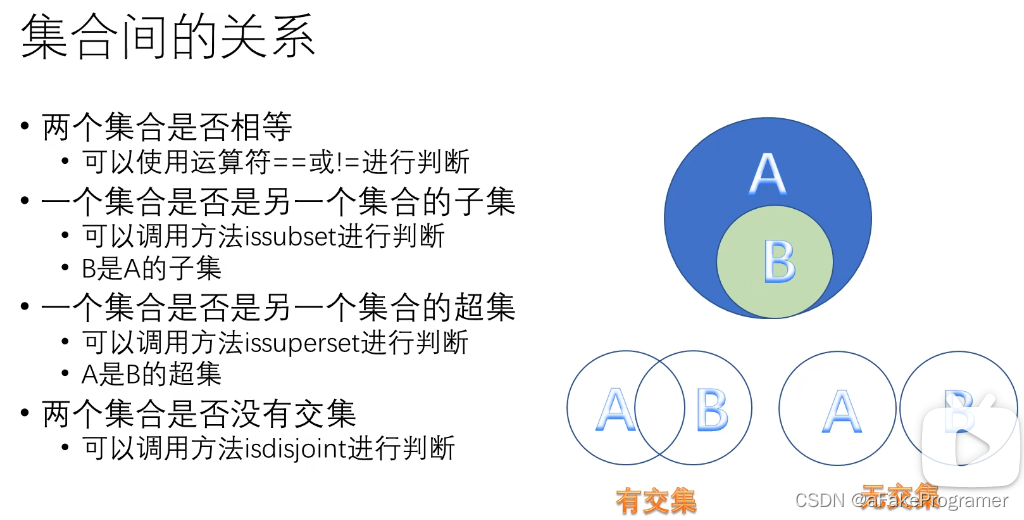
print('====集合的运算 集合是否相等=======')
s1={10,20,30,40}
s2={20,30,40,10}
print(s1==s2)#True  集合中元素是无序的，元素相同就相等
print(s1!=s2)#False

print('====集合的运算 集合是否子集=======')
s1={10,20,30,40,50,60}
s2={20,30,40,10}
s3={20,30,40,9}
print(s2.issubset(s1))#True
print(s3.issubset(s1))#False

print('====集合的运算 集合超集=======')
print(s1.issuperset(s2))
print(s1.issuperset(s3))
print('====集合的运算 集合交集=======')
print(s2.isdisjoint(s1))#False 有交集为False
s4={11,22,33,44}
print(s2.isdisjoint(s4))#True 没有交集为True

输出：

====集合的运算集合是否相等=======
True
False
====集合的运算集合是否子集=======
True
False
====集合的运算集合超集=======
True
False
====集合的运算集合交集=======
False
True

Process finished with exit code 0

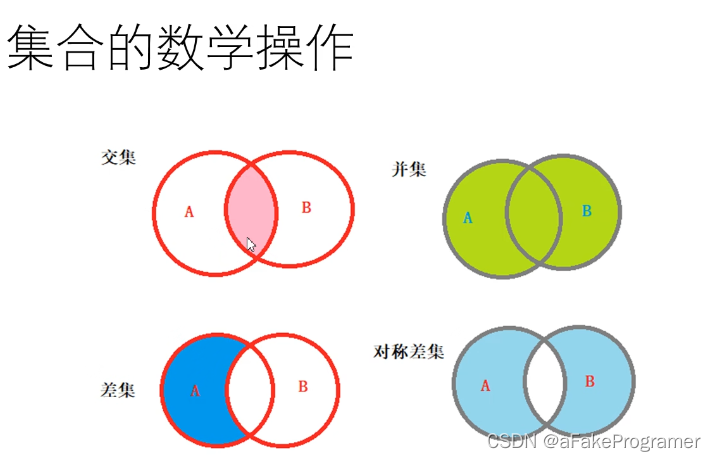
print('====集合的运算 2个集合的交集操作=======')
s1 = {10, 20, 30, 40, 50, 60}
s2 = {20, 30, 40, 10, 11}
print(s1.intersection(s2))  # {40, 10, 20, 30}
print(s1 & s2)  # 求交集 intersection(s2)与&是等价的
print('---------')
print(s1)
print(s2)
print('====集合的运算 2个集合的并集操作=======')
print(s1.union(s2))  # {40, 10, 11, 50, 20, 60, 30}
print(s1 | s2)  # 并集操作
print('---------')
print(s1)#{40, 10, 50, 20, 60, 30}
print(s2)#{40, 10, 11, 20, 30}
print('====集合的运算 2个集合的差集操作=======')
print(s1.difference(s2))#{50, 60}
print(s2 - s1 )#{11}
print('---------')
print(s1)
print(s2)

print('====集合的运算 2个集合的对称差集=======')
s1 = {10, 20, 30, 40, 50, 60}
s2 = {20, 30, 40, 10, 11}
print(s1.symmetric_difference(s2))#{50, 11, 60}

结果：

====集合的运算 2个集合的交集操作=======
{40, 10, 20, 30}
{40, 10, 20, 30}
---------
{40, 10, 50, 20, 60, 30}
{40, 10, 11, 20, 30}
====集合的运算 2个集合的并集操作=======
{40, 10, 11, 50, 20, 60, 30}
{40, 10, 11, 50, 20, 60, 30}
---------
{40, 10, 50, 20, 60, 30}
{40, 10, 11, 20, 30}
====集合的运算 2个集合的差集操作=======
{50, 60}
{11}
---------
{40, 10, 50, 20, 60, 30}
{40, 10, 11, 20, 30}
====集合的运算 2个集合的对称差集=======
{50, 11, 60}

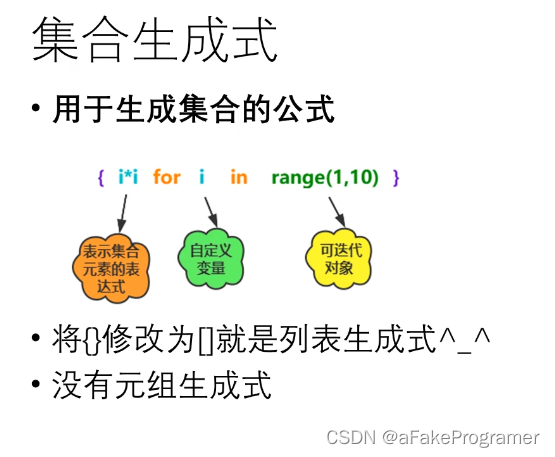
print('================集合生成式+++++++++++++++++++')
print('列表生成式')
lst =[ i*i for i in range(6)]
print(lst)#[0, 1, 4, 9, 16, 25]

print('集合生成式')
st ={ i*i for i in range(10)}#{0, 1, 64, 4, 36, 9, 16, 49, 81, 25}
print(st)