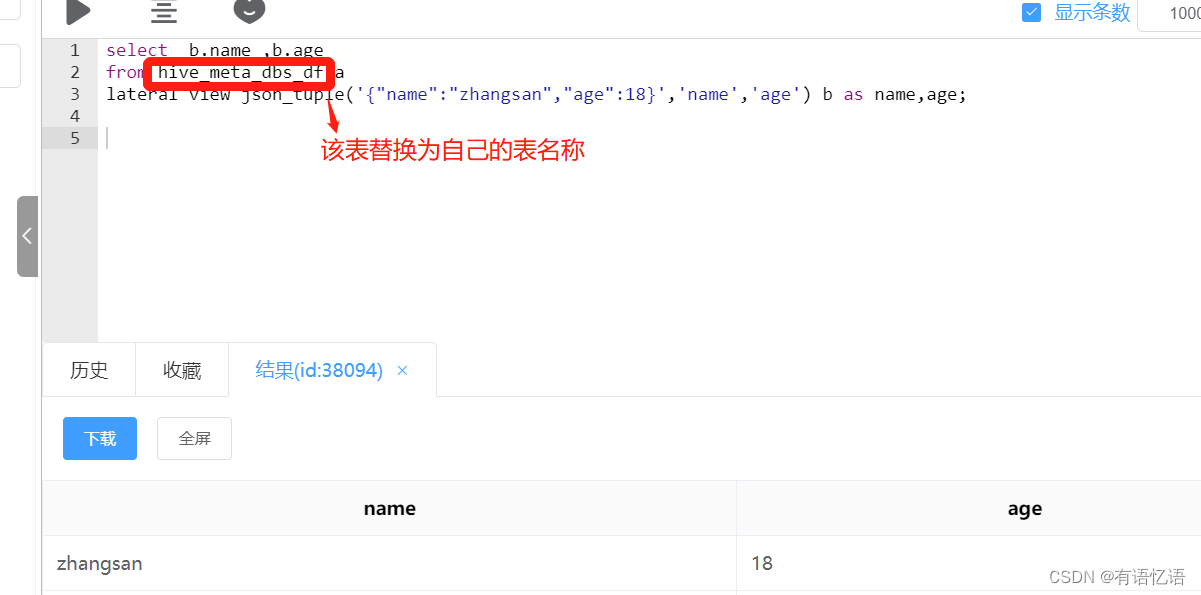
【立体视觉(三)】之张正友标定法原理
- 一、相机标定
- 二、参数求解
- 一)闭合解
- 二)极大似然解
- 三)考虑相机畸变
- 三、实验流程
此为个人学习笔记,在各处借鉴了不少好图好文(参考文献在文末),主要是对相关知识进行梳理,以期形成自己的体系。文字表述东拼西凑,符号公式手动输入,若有错误烦请指出。
一、相机标定
所谓标定(calibration),即是由大量观测值拟合参数模型的过程,且在此拟合的参数模型是已知的,所以应尽可能探索能便捷获取大量观测值的方案,如果观测值之间还满足一些其他的几何约束就更有助于求解具体单个参数值。
相机标定,目的是确定相机的内参矩阵
K
K
K,外参矩阵
R
、
T
R、T
R、T 和畸变系数
k
1
,
k
2
,
k
3
,
p
1
,
p
2
k_1,k_2,k_3,p_1,p_2
k1,k2,k3,p1,p2。
张氏标定法即提供了一种便捷获取大量观测值的的方案,同时观测值之间还满足一类明显的几何约束(即平面约束),可直接求解出内外参。其操作方式非常简单,只需要拍摄带有标定板图案的平面,即可完成相机标定,使标定难度极大降低,如果不追求高精度,打印一张棋盘格标定板图案粘贴到近似平的硬纸板上即可完成标定,加快了立体视觉的入门和普及,影响深远,是相机标定领域绝对的经典。
暂且先不考虑畸变系数,已知图像坐标
p
p
p 和世界坐标
P
w
P_w
Pw 之间通过内外参(投影矩阵)建立投影关系:
λ p = K [ R 3 × 3 T 3 × 1 ] [ P w 1 ] = M [ P w 1 ] \lambda {p}=K \begin{bmatrix} {R_{3\times3}}&{T_{3\times1}}\\ \end{bmatrix} \begin{bmatrix} {P_w}\\ {1}\\ \end{bmatrix}=M\begin{bmatrix} {P_w}\\ {1}\\ \end{bmatrix} λp=K[R3×3T3×1][Pw1]=M[Pw1]
用 r i r_i ri 表示旋转矩阵 R R R 的第 i i i 列,并用 t t t 代替 T 3 × 1 T_{3\times1} T3×1,假定模型平面在世界坐标系的 W = 0 W=0 W=0 平面上(为符号统一,在这里的世界坐标系与之前表述一致,为 P w ( U , V , W ) P_w(U,V,W) Pw(U,V,W) ),则
λ p = K [ r 1 r 2 r 3 t ] [ U V 0 1 ] = K [ r 1 r 2 t ] [ U V 1 ] \lambda {p}=K \begin{bmatrix} r_1&r_2&r_3&t\\ \end{bmatrix} \begin{bmatrix} U\\V\\0\\1 \end{bmatrix}= K \begin{bmatrix} r_1&r_2&t\\ \end{bmatrix} \begin{bmatrix} U\\V\\1 \end{bmatrix} λp=K[r1r2r3t] UV01 =K[r1r2t] UV1
如前所述,世界坐标系平面上的点与其图像上点通过单应矩阵相关:
λ
p
=
H
P
\lambda {p}=HP
λp=HP
此处,
p
=
[
u
,
v
,
1
]
T
p=[u,v,1]^T
p=[u,v,1]T,
P
=
[
U
,
V
,
1
]
P=[U,V,1]
P=[U,V,1],
H
=
R
[
r
1
,
,
r
2
,
t
]
H=R[r_1,,r_2,t]
H=R[r1,,r2,t] 为
3
×
3
3\times 3
3×3 矩阵。依然用
h
i
h_i
hi 来代表
H
H
H 中的第
i
i
i 列。有
[
h
1
,
h
2
,
h
3
]
=
Λ
K
[
r
1
,
r
2
,
t
]
[h_1,h_2,h_3]=\Lambda K[r_1,r_2,t]
[h1,h2,h3]=ΛK[r1,r2,t]
其中
Λ
\Lambda
Λ 是任意标量(
Λ
\Lambda
Λ 的存在是因为齐次坐标的尺度不变性,也可以认为其就等于1,在这里就让它为1,后面不管它了)。
r
1
r_1
r1 和
r
2
r_2
r2 是旋转矩阵
R
R
R 的列分量,是一对标准正交基。满足
r
1
T
r
2
=
0
,
r
1
T
r
1
=
r
2
T
r
2
=
1
r_1^Tr_2=0,r_1^Tr_1=r_2^Tr_2=1
r1Tr2=0,r1Tr1=r2Tr2=1。联系上式:
r
1
=
K
−
1
h
1
r
2
=
K
−
1
h
2
r_1=K^{-1}h_1\\r_2=K^{-1}h_2
r1=K−1h1r2=K−1h2
所以有:
h
1
T
K
−
T
K
−
1
h
2
=
0
h_1^TK^{-T}K^{-1}h_2=0
h1TK−TK−1h2=0
h
1
T
K
−
T
K
−
1
h
1
=
h
2
T
K
−
T
K
−
1
h
2
h_1^TK^{-T}K^{-1}h_1=h_2^TK^{-T}K^{-1}h_2
h1TK−TK−1h1=h2TK−TK−1h2
可以看出,单应矩阵 H H H 和内参矩阵 K K K 的元素之间满足两个线性方程约束。单应矩阵有 8 个自由度并且有 6 个外参(3 个用于旋转,3 个用于平移),我们只能获得对内参的 2 个约束。
二、参数求解
按论文结构,从解析解开始,然后是基于极大似然准则的非线性优化技术,最后考虑相机畸变。
一)闭合解
同样,用一个简单的矩阵替换上式中间的部分(常见操作),令
B
=
K
−
T
K
−
1
=
[
B
11
B
12
B
13
B
12
B
22
B
23
B
13
B
23
B
33
]
B=K^{-T}K^{-1}=\begin{bmatrix} B_{11}&B_{12}&B_{13}\\B_{12}&B_{22}&B_{23}\\B_{13}&B_{23}&B_{33}\\ \end{bmatrix}
B=K−TK−1=
B11B12B13B12B22B23B13B23B33
具体地:
B
=
[
1
f
x
2
−
s
f
x
2
f
y
v
0
s
−
u
0
f
y
f
x
2
f
y
−
s
f
x
2
f
y
s
2
f
x
2
f
y
2
+
1
f
y
2
−
s
(
v
0
s
−
u
0
f
y
f
x
2
f
y
2
)
−
v
0
f
y
2
v
0
s
−
u
0
f
y
f
x
2
f
y
−
s
(
v
0
s
−
u
0
f
y
)
f
x
2
f
y
2
−
v
0
f
y
2
(
v
0
s
−
u
0
f
y
)
2
f
x
2
f
y
2
+
v
0
2
f
y
2
+
1
]
B=\begin{bmatrix} \Large \frac{1}{f_x^2} & \Large -\frac{s}{f_x^2f_y} & \Large \frac{v_0s-u_0f_y}{f_x^2f_y}\\ \Large-\frac{s}{f_x^2f_y} &\Large \frac{s^2}{f_x^2f_y^2}+\frac{1}{f_y^2} &\Large -\frac{s(v_0s-u_0f_y}{f_x^2f_y^2)} -\frac{v_0}{f_y^2}\\ \Large \frac{v_0s-u_0f_y}{f_x^2f_y} & \Large -\frac{s(v_0s-u_0f_y)}{f_x^2f_y^2} -\frac{v_0}{f_y^2}& \Large\frac{(v_0s-u_0f_y)^2}{f_x^2f_y^2} +\frac{v_0^2}{f_y^2}+1\\ \end{bmatrix}
B=
fx21−fx2fysfx2fyv0s−u0fy−fx2fysfx2fy2s2+fy21−fx2fy2s(v0s−u0fy)−fy2v0fx2fyv0s−u0fy−fx2fy2)s(v0s−u0fy−fy2v0fx2fy2(v0s−u0fy)2+fy2v02+1
上文已设
H
H
H 的第
i
i
i 个列向量为
h
i
=
[
h
i
1
,
h
i
2
,
h
i
3
]
T
h_i=[h_{i1},h_{i2},h_{i3}]^T
hi=[hi1,hi2,hi3]T 。则有
h
i
T
B
h
j
=
[
h
i
1
h
i
2
h
i
3
]
[
B
11
B
12
B
13
B
12
B
22
B
23
B
13
B
23
B
33
]
[
h
j
1
h
j
2
h
j
3
]
=
[
h
i
1
B
11
+
h
i
2
B
12
+
h
i
3
B
13
h
i
1
B
12
+
h
i
2
B
22
+
h
i
3
B
23
h
i
1
B
13
+
h
i
2
B
23
+
h
i
3
B
33
]
[
h
j
1
h
j
2
h
j
3
]
h_i^TBh_j=\begin{bmatrix}h_{i1}&h_{i2}&h_{i3}\end{bmatrix} \begin{bmatrix} B_{11}&B_{12}&B_{13}\\B_{12}&B_{22}&B_{23}\\B_{13}&B_{23}&B_{33}\\ \end{bmatrix} \begin{bmatrix}h_{j1}\\h_{j2}\\h_{j3}\end{bmatrix} \\=\begin{bmatrix}h_{i1}B_{11}+h_{i2}B_{12}+h_{i3}B_{13}&h_{i1}B_{12}+h_{i2}B_{22}+h_{i3}B_{23}&h_{i1}B_{13}+h_{i2}B_{23}+h_{i3}B_{33}\end{bmatrix}\begin{bmatrix}h_{j1}\\h_{j2}\\h_{j3}\end{bmatrix}
hiTBhj=[hi1hi2hi3]
B11B12B13B12B22B23B13B23B33
hj1hj2hj3
=[hi1B11+hi2B12+hi3B13hi1B12+hi2B22+hi3B23hi1B13+hi2B23+hi3B33]
hj1hj2hj3
=
h
i
1
h
j
1
B
11
+
h
i
2
h
j
1
B
12
+
h
i
3
h
j
1
B
13
+
h
i
1
h
j
2
B
12
+
h
i
2
h
j
2
B
22
+
h
i
3
h
j
2
B
23
+
h
i
1
h
j
3
B
13
+
h
i
2
h
j
3
B
23
+
h
i
3
h
j
3
B
33
=h_{i1}h_{j1}B_{11}+h_{i2}h_{j1}B_{12}+h_{i3}h_{j1}B_{13}+h_{i1}h_{j2}B_{12}+h_{i2}h_{j2}B_{22}+h_{i3}h_{j2}B_{23}+h_{i1}h_{j3}B_{13}+h_{i2}h_{j3}B_{23}+h_{i3}h_{j3}B_{33}
=hi1hj1B11+hi2hj1B12+hi3hj1B13+hi1hj2B12+hi2hj2B22+hi3hj2B23+hi1hj3B13+hi2hj3B23+hi3hj3B33
=
[
h
i
1
h
j
1
h
i
1
h
j
2
+
h
i
2
h
j
1
h
i
2
h
j
2
h
i
3
h
j
1
+
h
i
1
h
j
3
h
i
3
h
j
2
+
h
i
2
h
j
3
h
i
3
h
j
3
]
[
B
11
B
12
B
22
B
13
B
23
B
33
]
=\begin{bmatrix}h_{i1}h_{j1}&h_{i1}h_{j2}+h_{i2}h_{j1}&h_{i2}h_{j2}&h_{i3}h_{j1}+h_{i1}h_{j3}&h_{i3}h_{j2}+h_{i2}h_{j3}&h_{i3}h_{j3}\end{bmatrix}\begin{bmatrix}B_{11}\\B_{12} \\B_{22}\\B_{13} \\B_{23} \\B_{33}\end{bmatrix}
=[hi1hj1hi1hj2+hi2hj1hi2hj2hi3hj1+hi1hj3hi3hj2+hi2hj3hi3hj3]
B11B12B22B13B23B33
令
b
=
[
B
11
,
B
12
,
B
22
,
B
13
,
B
23
,
B
33
]
T
b=[B_{11} ,B_{12} ,B_{22},B_{13} ,B_{23} ,B_{33}]^T
b=[B11,B12,B22,B13,B23,B33]T
v
i
j
=
[
h
i
1
h
j
1
,
h
i
1
h
j
2
+
h
i
2
h
j
1
,
h
i
2
h
j
2
,
h
i
3
h
j
1
+
h
i
1
h
j
3
,
h
i
3
h
j
2
+
h
i
2
h
j
3
,
h
i
3
h
j
3
]
T
v_{ij}=[h_{i1}h_{j1},h_{i1}h_{j2}+h_{i2}h_{j1},h_{i2}h_{j2},h_{i3}h_{j1}+h_{i1}h_{j3},h_{i3}h_{j2}+h_{i2}h_{j3},h_{i3}h_{j3}]^T
vij=[hi1hj1,hi1hj2+hi2hj1,hi2hj2,hi3hj1+hi1hj3,hi3hj2+hi2hj3,hi3hj3]T
则有:
h
i
T
B
h
j
=
v
i
j
T
b
h_i^TBh_j=v_{ij}^Tb
hiTBhj=vijTb
(注:原论文直接给出了上面这个式子,给我看楞了,才发现这个式子不是推导的,而是先计算再提取的系数,所以这里我选择推算一遍,有助于理解。)
h
i
T
B
h
j
=
v
i
j
T
b
h_i^TBh_j=v_{ij}^Tb
hiTBhj=vijTb
再联系以上单应矩阵
H
H
H 和内参矩阵
K
K
K 的元素之间满足两个线性方程约束,有
[
v
11
T
(
v
11
−
v
22
)
T
]
b
=
0
\begin{bmatrix}v_{11}^T\\(v_{11}-v_{22})^T\end{bmatrix}b=0
[v11T(v11−v22)T]b=0
当相机在1个位姿下拍摄标定板图案后,经过角点的像素坐标提取,可得所有角点的世界坐标系和像素坐标系的对应关系,进而通过线性方程组的最小二乘解法求解当前位姿下的单应矩阵
H
H
H ,可得以上公式。但其只有两行,用来求解6维的
b
b
b 向量至少需要3个单应矩阵,即至少需要3张图片才能完成相机标定,总方程组可表达为:
V
b
=
0
Vb=0
Vb=0
- 如果图片数量为 n ≥ 3 n≥3 n≥3 ,通常可以获得 b b b 的一个唯一解(由于尺度等价性,求出的 b b b 的任意倍数仍是正确解)。
- 如果图片数量为 n = 2 n=2 n=2,可以施加无偏约束 s = 0 s=0 s=0,将 [ 0 , 1 , 0 , 0 , 0 , 0 ] b [0,1,0,0,0,0]b [0,1,0,0,0,0]b 作为附加方程添加到上式中。
- 如果图片数量为 n = 2 n=2 n=2,可以假设 u 、 v 0 、 s u_、v_0、s u、v0、s 已知(比如说都为0),将 f x 、 f y f_x、f_y fx、fy 求解出来。
求解出 b b b后,就可以按如下方式计算所有相机内在参数(因为由 b b b 组成的矩阵 B B B 不严格满足 B = K − T K − 1 B=K^{-T}K^{-1} B=K−TK−1,而是存在一个任意的尺度因子 λ \lambda λ (又来了)满足 B = λ K − T K − 1 B=\lambda K^{-T}K^{-1} B=λK−TK−1):
v
0
=
B
12
B
13
−
B
11
B
23
B
11
B
22
−
B
22
2
v_0=\frac{B_{12}B_{13}-B_{11}B_{23}}{B_{11}B_{22}-B_{22}^2}
v0=B11B22−B222B12B13−B11B23
λ
=
B
33
−
B
13
2
+
v
0
(
B
12
B
13
−
B
11
B
23
)
B
11
\lambda =B_{33}-\frac{B_{13}^2+v_0(B_{12}B_{13}-B_{11}B_{23})}{B_{11}}
λ=B33−B11B132+v0(B12B13−B11B23)
f
x
=
λ
B
11
f_x=\sqrt{\frac{\lambda }{B_{11}}}
fx=B11λ
f
y
=
λ
B
11
B
11
B
22
−
B
22
2
f_y=\sqrt{\frac{\lambda B_{11}}{B_{11}B_{22}-B_{22}^2}}
fy=B11B22−B222λB11
s
=
−
B
12
f
x
2
f
y
λ
s=-\frac{B_{12}f_x^2f_y}{\lambda}
s=−λB12fx2fy
u
0
=
s
v
0
f
x
−
B
13
f
x
2
λ
u_0=\frac{sv_0}{f_x}-\frac{B_{13}f_x^2}{\lambda}
u0=fxsv0−λB13fx2
当内参矩阵
K
K
K 求解出后,每个位姿的外参矩阵
R
、
T
R、T
R、T 可以进一步求出:
r
1
=
λ
K
−
1
h
1
r
2
=
λ
K
−
1
h
2
r
3
=
r
1
×
r
2
t
=
λ
K
−
1
h
3
r_1=\lambda K^{-1}h_1\\ r_2=\lambda K^{-1}h_2\\ r_3=r_1 \times r_2\\ t=\lambda K^{-1}h_3
r1=λK−1h1r2=λK−1h2r3=r1×r2t=λK−1h3
其中,
λ
=
1
∣
∣
K
−
1
h
1
∣
∣
=
1
∣
∣
K
−
1
h
2
∣
∣
\lambda=\frac{1}{|| K^{-1}h_1 ||}=\frac{1}{|| K^{-1}h_2 ||}
λ=∣∣K−1h1∣∣1=∣∣K−1h2∣∣1。由于数据中存在噪声,因此计算出的矩阵
R
R
R 通常不满足旋转矩阵的性质,可以通过奇异值分解来获得最佳旋转矩阵。
二)极大似然解
上述解是通过最小化一个没有物理意义的代数距离得到的,由于噪声的存在,其解并不会非常精确。我们可以通过最大似然估计法来获取更精确的解。
给定标定板平面的
n
n
n 个图像,模型平面上有
m
m
m 个点。假设图像点的噪声独立且同分布。可以通过最小化以下函数来获得极大似然估计:
∑ i = 1 n ∑ j = 1 m ∣ ∣ p i j − p ^ ( K , R i , t i , P j ) ∣ ∣ 2 \sum\limits_{i=1}^{n}\sum\limits_{j=1}^{m}||p_{ij}-\hat p(K,R_i,t_i,P_j)||^2 i=1∑nj=1∑m∣∣pij−p^(K,Ri,ti,Pj)∣∣2
其中 p ^ ( K , R i , t i , P j ) \hat p(K,R_i,t_i,P_j) p^(K,Ri,ti,Pj) 是空间点 P j P_j Pj 在图像 i i i 上的投影点。旋转矩阵 R R R 可由三个向量 r r r 表示, r r r平行于旋转轴并且其大小(模长)等于旋转角。 R R R 和 r r r 通过 Rodrigues (罗德里格斯)公式联系起来。对上式最小化是一个非线性最小化问题,可用 Levenberg-Marquardt 算法求解。该类问题需要有一个较准确的初始值,可以用上文所提到的闭合解来作为初始值。
三)考虑相机畸变
在前文中有提到,畸变校正时一般会考虑3个径向畸变参数
k
1
、
k
2
、
k
3
k_1、k_2、k_3
k1、k2、k3 和2个切向畸变参数
p
1
、
p
2
p_1、p_2
p1、p2,在张氏标定中,只考虑了2个径向畸变参数
k
1
、
k
2
k_1、k_2
k1、k2。实际应用时会考虑更多项,原理相同。
精准的未畸变坐标在内外参未知时是无法计算的(观测值总是有误差的),但在估计内外参时又没有考虑畸变参数(咬尾巴了)。无所谓,概念论会出手:将闭合解得到的内外参作为初始值,求出近似理想坐标,然后根据畸变校正公式建立线性方程组来求解近似的
k
1
、
k
2
k_1、k_2
k1、k2 作为以下极大似然估计的初始值:
∑
i
=
1
n
∑
j
=
1
m
∣
∣
p
i
j
−
p
^
(
K
,
k
1
,
k
2
,
R
i
,
t
i
,
P
j
)
∣
∣
2
\sum\limits_{i=1}^{n}\sum\limits_{j=1}^{m}||p_{ij}-\hat p(K,k_1,k_2,R_i,t_i,P_j)||^2
i=1∑nj=1∑m∣∣pij−p^(K,k1,k2,Ri,ti,Pj)∣∣2
通过非线性求解方法来求解所有内外参数和畸变系数。
实际上,因为畸变系数值很小,所以直接将畸变系数的初值全部设置为0也是可以的,这就不需要解线性方程组了。
三、实验流程
总结一下张氏标定流程:
- 打印标定图案并粘贴至一个平面上,称之为标定板。
- 通过移动相机或移动标定板在不同的位姿拍摄多张标定板图像(图像数>=3)。
- 在所有图像上检测特征点(角点或者圆心点)。
- 使用闭合解法求解所有内参外参。
- 通过非线性优化计算精确的内外参数和畸变系数(畸变系数初始值可通过畸变校正线性方程组求解或直接赋值为0)。


纸上得来终觉浅,后续考虑上手实践一下。
参考:
[1] Zhang Z . A Flexible New Technique for Camera Calibration[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2000, 22(11):1330-1334.
[2] 立体视觉入门指南(3):相机标定之Zhang式标定法
[3] Calibration Patterns Explained









![[Eigen中文文档] 稠密矩阵分解函数对比](https://img-blog.csdnimg.cn/281b570fcc6542c18cf73cf1ad3151fe.png#pic_center)