⭐️前言⭐️
本篇文章是从暴力递归到动态规划的第三章。
🍉欢迎点赞 👍 收藏 ⭐留言评论 📝私信必回哟😁
🍉博主将持续更新学习记录收获,友友们有任何问题可以在评论区留言
🍉博客中涉及源码及博主日常练习代码均已上传GitHub

📍内容导读📍
- 🍅最小距离和
- 🍅目标货币值
- 🍅目标货币值2
- 🍅目标货币值3
- 🍅醉汉走路
🍅最小距离和
题目:
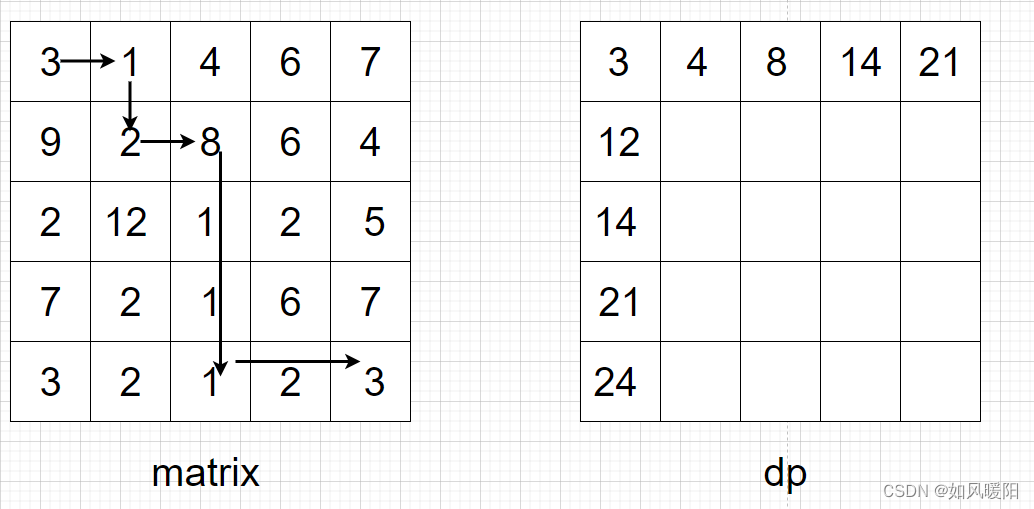
给定一个二维数组matrix,一个人必须从左上角出发,最后到达右下角
沿途只可以向下或者向右走,沿途的数字都累加就是距离累加和
返回最小距离累加和
题解思路:
根据matrix表构建出dp表,dp表中数字的含义是从[0,0]位置到该位置的最短距离,dp表中的第一行只能依靠左边来得出,dp表中的第一列只能依靠上边来得出,其余位置的结果依赖左边和上边较小的数值,最后返回dp表右下角的结果即为所求。
代码实现:
public class MinPathSum {
public static int minPathSum(int[][] m) {
if(m==null||m.length==0||m[0]==null||m[0].length==0) {
return 0;
}
int row=m.length;
int col=m[0].length;
int[][] dp=new int[row][col];
dp[0][0]=m[0][0];
for (int i = 1; i < row; i++) {
dp[i][0]=dp[i-1][0]+m[i][0];
}
for (int j = 1; j < col; j++) {
dp[0][j]=dp[0][j-1]+m[0][j];
}
for (int i = 1; i < row; i++) {
for (int j = 1; j < col; j++) {
dp[i][j]=Math.min(dp[i-1][j],dp[i][j-1])+m[i][j];
}
}
return dp[row-1][col-1];
}
}
题解思路2:(状态压缩)
如果matrix表非常大,那么对应的dp表也将会非常大,为了节省空间,可以通过一个一维数组来完成状态压缩,通过一行行更新数值的方式,到达最后一行的dp状态,返回最后结果。
首先第一行的状态都依赖于左边的数值,先完成第一行的初始化;往下的行中第一列,依赖于上边的值,此时数组中记录的就是上边的值,直接相加即可;然后右移,此时该位置的结果为上一行的结果,左边也刚完成更新,两者取较小再相加matrix中此位置的值即可。
代码实现:
public class MinPathSum {
public static int minPathSum2(int[][] m) {
if(m==null||m.length==0||m[0]==null||m[0].length==0) {
return 0;
}
int row=m.length;
int col=m[0].length;
int[] dp=new int[col];
dp[0]=m[0][0];
for (int j = 1; j < col; j++) {
dp[j]=dp[j-1]+m[0][j];
}
for (int i = 1; i < row; i++) {
dp[0]+=m[i][0];
for (int j = 1; j < col; j++) {
dp[j]=Math.min(dp[j-1],dp[j])+m[i][j];
}
}
return dp[col-1];
}
}
🍅目标货币值
题目:
arr是货币数组,其中的值都是正数。再给定一个正数aim。
每个值都认为是一张货币,
即便是值相同的货币也认为每一张都是不同的,
返回组成aim的方法数
例如:arr = {1,1,1},aim = 2
第0个和第1个能组成2,第1个和第2个能组成2,第0个和第2个能组成2
一共就3种方法,所以返回3
题解思路1:
从左往右的尝试模型,每个位置考虑要或者不要,由两个变量确定终止条件,返回最终的结果。
代码实现:
public class CoinsWayEveryPaperDifferent {
public static int coinWays(int[] arr,int aim) {
return process(arr,0,aim);
}
// arr[index...] 组成正好rest这么多的钱,有几种方法
public static int process(int[] arr,int index,int rest) {
if(rest<0) {
return 0;
}
if(index==arr.length) {
return rest==0? 1: 0;
}else {
return process(arr,index+1,rest)+process(arr,index+1,rest-arr[index]);
}
}
}
题解思路2:
由暴力递归演变到动态规划,观察依赖关系,都是依赖index+1后一个位置的结果,所以dp表先完成后边的填写,再往前递推。
代码实现:
public class CoinsWayEveryPaperDifferent {
public static int dp(int[] arr,int aim) {
if(aim==0) {
return 1;
}
int N=arr.length;
int[][] dp=new int[N+1][aim+1];
dp[N][0]=1;
for (int index = N-1; index >=0 ; index--) {
for (int rest = 0; rest <=aim ; rest++) {
dp[index][rest]=dp[index+1][rest]+(rest-arr[index]>=0?dp[index+1][rest-arr[index]]:0);
}
}
return dp[0][aim];
}
}
🍅目标货币值2
题目:
arr是面值数组,其中的值都是正数且没有重复。再给定一个正数aim。
每个值都认为是一种面值,且认为张数是无限的。
返回组成aim的方法数
例如:arr = {1,2},aim = 4
方法如下:1+1+1+1、1+1+2、2+2
一共就3种方法,所以返回3
题解思路1:
依然是从左往右的模型,依次考虑每个位置面值的张数情况,从而确定方法数。
代码实现:
public class CoinsWayNoLimit {
public static int coinsWay(int[] arr,int aim) {
if(arr==null || arr.length==0 || aim<0) {
return 0;
}
return process(arr,0,aim);
}
// arr[index...]所有的面值,每一个面值都可以任意选择张数,组成正好rest这么多钱,求方法数有多少?
public static int process(int[] arr,int index,int rest) {
if(index==arr.length) {
return rest==0?1:0;
}
int ways=0;
for (int pages = 0; pages*arr[index] <=rest ; pages++) {
ways+=process(arr,index+1,rest-(pages*arr[index]));
}
return ways;
}
}
题解思路2:
根据暴力递归的尝试,转化为动态转移方法,根据严格依赖的表关系,得出最后的结果。
代码实现:
public class CoinsWayNoLimit {
public static int dp(int[] arr,int aim) {
if(arr==null||arr.length==0||aim<0) {
return 0;
}
int N=arr.length;
int[][] dp=new int[N+1][aim+1];
dp[N][0]=1;
for (int index = N-1; index >=0 ; index++) {
for (int rest = 0; rest <=aim; rest++) {
int ways=0;
for (int pages = 0; (pages*arr[index]) <=rest ; pages++) {
ways+=dp[index+1][rest-(pages*arr[index])];
}
dp[index][rest]=ways;
}
}
return dp[0][aim];
}
}
题解思路3:
由于每个位置的dp结果,依赖于for循环的多个结果,可以通过记忆化搜索的方式再进一步优化,如下所示:
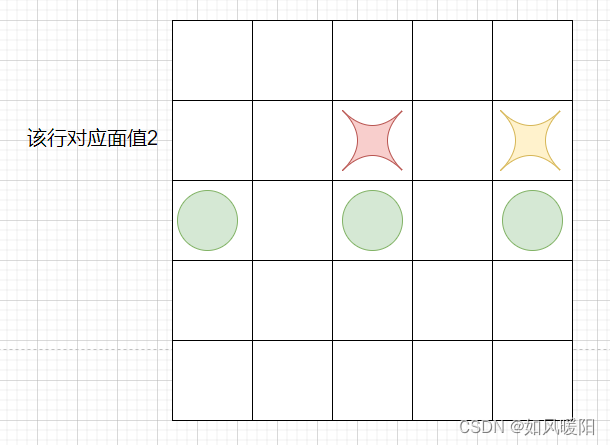
假设星所在行对应的面值为2,那么黄星依赖于下边三个圆圈的结果;红星依赖于第一个和第二个结果,所以黄星可以通过红星+dp[index+1][rest]得到,而避免再去通过for循环来计算。
代码实现:
public class CoinsWayNoLimit {
public static int dp2(int[] arr,int aim) {
if(arr==null||arr.length==0||aim<0) {
return 0;
}
int N=arr.length;
int[][] dp=new int[N+1][aim+1];
dp[N][0]=1;
for (int index = N-1; index >=0 ; index--) {
for (int rest = 0; rest <=aim ; rest++) {
dp[index][rest]=dp[index+1][rest];
if(rest-arr[index]>=0) {// 不越界就加
dp[index][rest]+=dp[index][rest-arr[index]];
}
}
}
return dp[0][aim];
}
}
🍅目标货币值3
题目:
arr是货币数组,其中的值都是正数。再给定一个正数aim。
每个值都认为是一张货币,
认为值相同的货币没有任何不同,
返回组成aim的方法数
例如:arr = {1,2,1,1,2,1,2},aim = 4
方法:1+1+1+1、1+1+2、2+2
一共就3种方法,所以返回3
题解思路:
该题就是目标货币值2加了限制条件,每个货币不是无限张了,而是有限张数。
代码实现:
public class CoinsWaySameValueSamePapper {
public static class Info {
public int[] coins;
public int[] pages;
public Info(int[] coins, int[] pages) {
this.coins = coins;
this.pages = pages;
}
}
public static Info getInfo(int[] arr) {
HashMap<Integer,Integer> counts=new HashMap<>();
for (int value:arr) {
if(!counts.containsKey(value)) {
counts.put(value,1);
}else {
counts.put(value,counts.get(value)+1);
}
}
int N=counts.size();
int[] coins=new int[N];
int[] pages=new int[N];
int index=0;
for (Map.Entry<Integer,Integer> entry: counts.entrySet()) {
coins[index]=entry.getKey();
pages[index++]= entry.getValue();
}
return new Info(coins,pages);
}
public static int coinsWay(int[] arr,int aim) {
if(arr==null||arr.length==0||aim<0) {
return 0;
}
Info info=getInfo(arr);
return process(info.coins,info.pages,0,aim);
}
// coins 面值数组,正数且去重
// pages 每种面值对应的张数
public static int process(int[] coins,int[] pages,int index,int rest) {
if(index==coins.length) {
return rest==0?1:0;
}
int ways=0;
for (int page=0;page*coins[index]<=rest&&page<=pages[index];page++) {
ways+=process(coins,pages,index+1,rest-(page*coins[index]));
}
return ways;
}
public static int dp1(int[] arr,int aim) {
if(arr==null||arr.length==0||aim<0) {
return 0;
}
Info info=getInfo(arr);
int[] coins= info.coins;
int[] pages= info.pages;
int N=coins.length;
int[][] dp=new int[N+1][aim+1];
dp[N][0]=1;
for (int index = N-1; index >=0 ; index--) {
for (int rest = 0; rest <=aim ; rest++) {
int ways=0;
for (int page = 0; page*coins[index]<=rest&&page<=pages[index] ; page++) {
ways+=dp[index+1][rest-page*coins[index]];
}
dp[index][rest]=ways;
}
}
return dp[0][aim];
}
public static int dp2(int[] arr,int aim) {
if(arr==null||arr.length==0||aim<0) {
return 0;
}
Info info=getInfo(arr);
int[] coins= info.coins;
int[] pages=info.pages;
int N=coins.length;
int[][] dp=new int[N+1][aim+1];
dp[N][0]=1;
for (int index = N-1; index >=0 ; index--) {
for (int rest = 0; rest <=aim ; rest++) {
dp[index][rest]=dp[index+1][rest];
if(rest-coins[index]>=0) {
dp[index][rest]+=dp[index][rest-coins[index]];
}
// 如果记忆化搜索可能会多算,再把多算的减掉即可
if(rest-coins[index]*(pages[index]+1)>=0) {
dp[index][rest]-=dp[index+1][rest-coins[index]*(pages[index]+1)];
}
}
}
return dp[0][aim];
}
}
🍅醉汉走路
题目:
给定5个参数,N,M,row,col,k
表示在NM的区域上,醉汉Bob初始在(row,col)位置
Bob一共要迈出k步,且每步都会等概率向上下左右四个方向走一个单位
任何时候Bob只要离开NM的区域,就直接死亡
返回k步之后,Bob还在N*M的区域的概率
题解思路:
每个位置可以走向四个方向,总结果数为4^k,如果走完K步,没有走出N*M区域,就返回一种结果,最后得出生存点数除以总结果数,即为所求。
代码实现:
public class BobDie {
public static double livePosibility1(int row,int col,int k,int N,int M) {
return (double) process(row,col,k,N,M)/Math.pow(4,k);
}
// 目前在row,col位置,还有rest步要走,走完了如果还在棋盘中就获得1个生存点,返回总的生存点数
public static long process(int row,int col,int rest,int N,int M) {
if(row<0||row==N||col<0||col==M) {
return 0;
}
if(rest==0) {
return 1;
}
long up=process(row-1,col,rest-1,N,M);
long down=process(row+1,col,rest-1,N,M);
long left=process(row,col-1,rest-1,N,M);
long right=process(row,col+1,rest-1,N,M);
return up+down+left+right;
}
}
题解思路2:
根据暴力递归转化为动态规划,可变参数有row、col、rest三个,建立一个三维dp表,根据依赖关系记录每个位置的结果,最后返回结果。
代码实现:
public class BobDie {
public static double livePosibility2(int row,int col,int k,int N,int M) {
long[][][] dp=new long[N][M][k+1];
for (int i = 0; i < N; i++) {
for (int j = 0; j < M; j++) {
dp[i][j][0]=1;
}
}
for (int rest = 1; rest <=k ; rest++) {
for (int r = 0; r < N; r++) {
for (int c = 0; c < M; c++) {
dp[r][c][rest]=pick(dp,N,M,r-1,c,rest-1);
dp[r][c][rest]+=pick(dp,N,M,r+1,c,rest-1);
dp[r][c][rest]+=pick(dp,N,M,r,c-1,rest-1);
dp[r][c][rest]+=pick(dp,N,M,r,c+1,rest-1);
}
}
}
return (double)dp[row][col][k]/Math.pow(4,k);
}
public static long pick(long[][][] dp,int N,int M,int r,int c,int rest) {
if(r<0||r==N||c<0||c==M) {
return 0;
}
return dp[r][c][rest];
}
}
⭐️最后的话⭐️
总结不易,希望uu们不要吝啬你们的👍哟(^U^)ノ~YO!!如有问题,欢迎评论区批评指正😁