何为快速幂？

我们经常会计算：。STL中有自带的pow函数，如果当n很大的时候，那么一定会TLE。

因此，我们需要另一种求值的方法：快速幂！

快速幂有两种做法：1：递归        2：迭代                                ps：我目前只知道有两种...(蒟蒻..)

这里我们讲的是迭代这种方法：

我们以进行分析：

注意：指数前的“+”，表示该指数是由上一个指数翻倍+1后得到的。

（相当于：,3是由1翻倍后+1得到的）

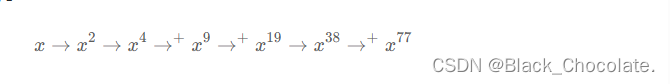
在这个过程中：我们从左往右进行演变，很难发现规律。因为在某一过程中，不仅是指数翻倍，而且翻倍后还加了1.因此我们选择从右往左进行演变。

我们把这些贡献值相乘起来会得到：

看到这里，可能大家还是有点懵，但是接下来各位一定会豁然开朗。

我相信某些读者应该想到了：在相乘的过程中，指数都是2的倍数，因此我们可以试着用二进制来表示表示。

结果我们发现：77的二进制：1001101。

正好依次对应指数值：               

因此指数我们可以拆分为：

 

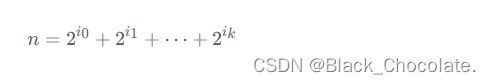
即：

 

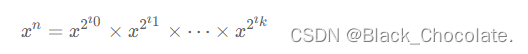
代码：

int quickpow(int x,int n){//n为指数
	int ans=1;//记录答案
	while(n){//判断指数
		if(n&1) ans*=x;//如果指数的最低位为1，则进行累计操作（相当于乘法过程的乘）
		x*=x;//每移一位，相当于x^2，即：x*=x（翻倍）
        n>>=1;//判断下一位
	}
	return ans;
}

//这段代码没有考虑溢出的问题：
//Mod=1e9+7
//解决这个问题也很简单：在ans*=x的后面紧接一个取余操作即可：ans%=Mod，在x*=x的后面紧接一句：x%=Mod即可