多边形三角化，简单来说，就是给定一圈有序的多边形点生成三角面片，EarCut的原理描述网络上有很多（如https://blog.csdn.net/qq_24459491/article/details/102976671），就不细说了。但是有的时候看是一回事，源码写是另一回事，实践才是学习的最好方法，所以本文对mapbox 开源的Earcut算法进行剖析（github地址：https://github.com/mapbox/earcut）。

首先说一下Ear在程序中的判断依据：Ear点是多边形中的凸点并且它和它相邻的两个顶点组成的三角形内部不包括包括多边形的其他顶点。Mapbox中定义如下：

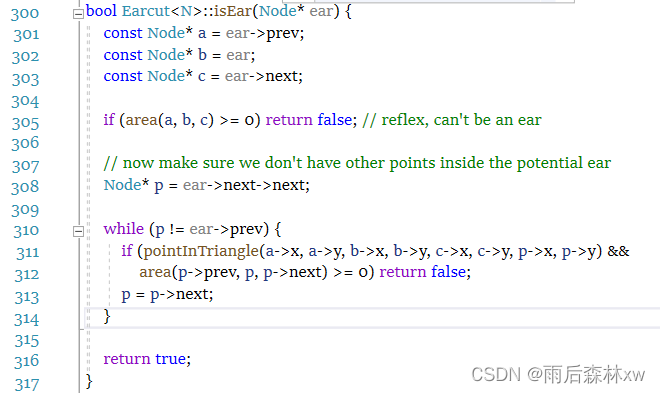
其中305行就是在判断顶点是否为凸点，这是通过与其相邻顶点的法线方向来判断。这里多边形顶点顺序是顺时针，所以判断法线方向为负就是凸点（对于二维多边形来说，两条边的叉积就是两条边组成的平行四边形的有向面积）。

310到313行就是在遍历多边形的顶点，判断是否有其他顶点在三角形内。Earcut算法的复杂度为n*n,平方就是从这儿来的。

判断顶点是否在三角形内部的原理就很简单了，mapbox三角形按逆时针排列，所以判断依次两两顶点与该点组成的三角形是否法线均为正。

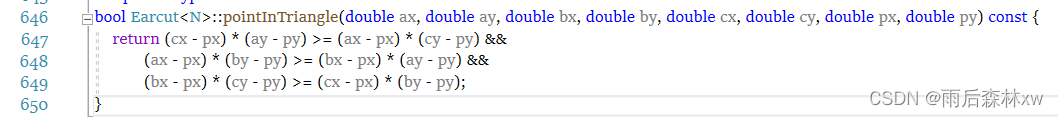
如果三角形顺序随机，判断三个三角形的法线是否一致也可。

由上面看到，判断Ear, 要判断顶点为凸点的前提是要知道多边形是按逆时针还是顺时针排列，mapbox以格林公式来判断多边形的时针顺序。

还有一种方式是通过多边形叉积求有向面积的方式：

 这里有向面积是该顶点和下一个顶点，原点组成的三角形面积和。

有了顶点顺序，就可以判断Ear，然后就可以选择三角面的三个顶点了，即Ear和它的相邻两个顶点。然后删除Ear,剩余多边形继续相同操作，直至小于3个点。

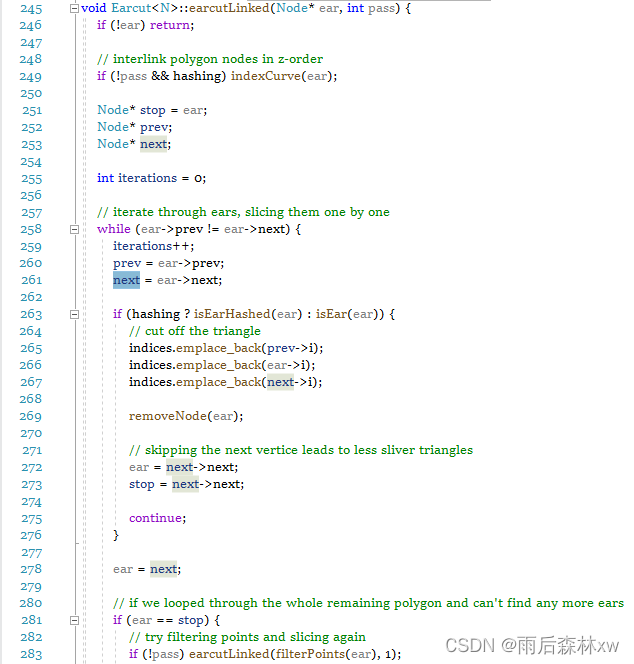
其中283行fileterPoints用于删除共线和重复点。

另外，我们可以看到，249行怎么还有indexCurve，isEar也有不同的判断函数isEarHashed？这是因为mapbox还对Earcut进行了效率优化，是否使用效率优化MapBox是通过判断顶点的个数是否大于80个。

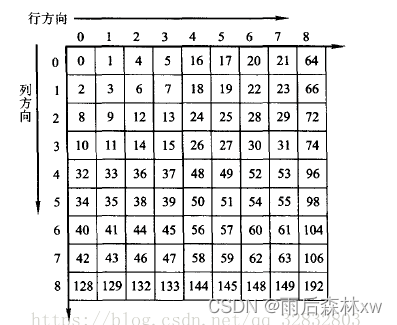
那哪里还有优化空间？在判断isEar的时候，mapbox遍历了所有顶点来判断是否有顶点在三角形内，其实三角形box范围内搜索就足够了，那么怎么来缩小这个搜索范围，毕竟是个二维数据，mapbox应用了z-order算法将二维数据映射到一维的方式，然后排序缩小了顶点的搜索范围。

z-order是一种莫顿码编码（Morton Code)方式, 将两个十进制转换成二进制，然后位数两两交叉，就得到了二进制的莫顿码(莫顿码也支持3维，计算方式类似）。

Mapbox计算方式如下：

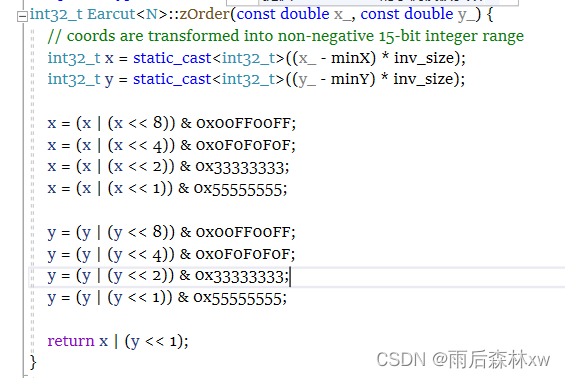
其中minX是所有顶点的最小x值，minY是所有顶点的最小Y值。inv_size用于将坐标值转为整数用于z_order计算（最大为15位）

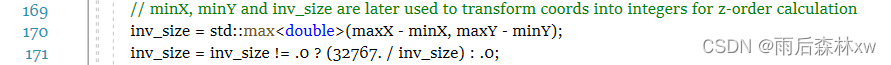
这里z_order计算用得是Magic Bits方法，可能不好理解，用另一种FOR_LOOP方法就好理解了。

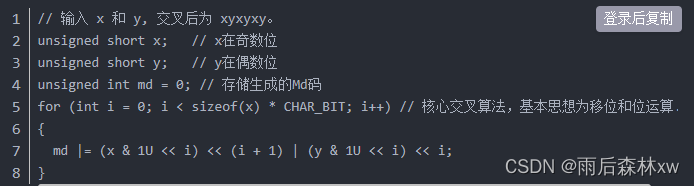
CHAR_BIT =8位

有了zorder,链表按Morton 排序，然后替换掉isEar里面遍历所有顶点的部分就是isEarHashed。

 

Mapbox EarCut还包括了对洞的处理，需要进一步剖析。