图的相关概念

图的定义：一组（V，E）对。
V：一个点集的集合。
E：边集，呈现形式为V上的一个关系。什么是关系

V的一个例子为{x₁，x₂，x₃}，E的一个例子为{（x₁，x₂），（x₂，x₃）}，也可写成{x₁-x₂，x₂-x₃}。

相邻点：如果两个点之间有边，那么这两个点就是相邻的。
映射：如果（x₁，x₂）是E的一个元素，那么E映射到x₁，E也映射到x₂。
度数：边集映射到x₁的次数称为x₁的度数。
环：起点和终点都是同一个点的边称为环。
重边：两个起点和终点完全相同的边称为重边。
简单图：没有环或者重边的图称作简单图。

涂色问题

给定一个图，如果最少能用K种颜色为图涂色，使相邻点拥有不同颜色，那么K称为该图的色度。

基础涂色方法（贪婪算法）

步骤：

将点标号为x₁，x₂，…，x_n。
将颜色标号为c₁，c₂，…，c_n。
每次用标号最小的合法颜色涂标号最小的尚未上色的点。

易证：使用这种算法，如果图中度数最多的点有d度，那么最多使用（d+1）种颜色。

证明

可以用归纳法证明，设P_n表示有n个点的图满足命题：

基础步骤：n=1时，d=0，用一种颜色，P₁=T。
归纳步骤：假设P_n=T，考虑有（n+1）个点的图，该图中的点最多拥有d度。若在该图中取走一个点，那么剩下的n点图中的点也最多拥有d度且一定满足P_n。再加回该点，即使该点拥有d度，且相连的d个点颜色都不同，该点也可以使用第（d+1）种颜色，因此（n+1）点图的色度<=（d
+1），P_n+1=T。□

二分图

如果一个图可以分成左右两个集合，集合内部的点都不相邻，分属于两个集合的部分点有相邻关系，那么这个图称为二分图。不难看出，二分图色度为2。

匹配问题

匹配：给定一个图，这个图的一个所有点都有且只有1度的子图称作该图的一个匹配。例如：

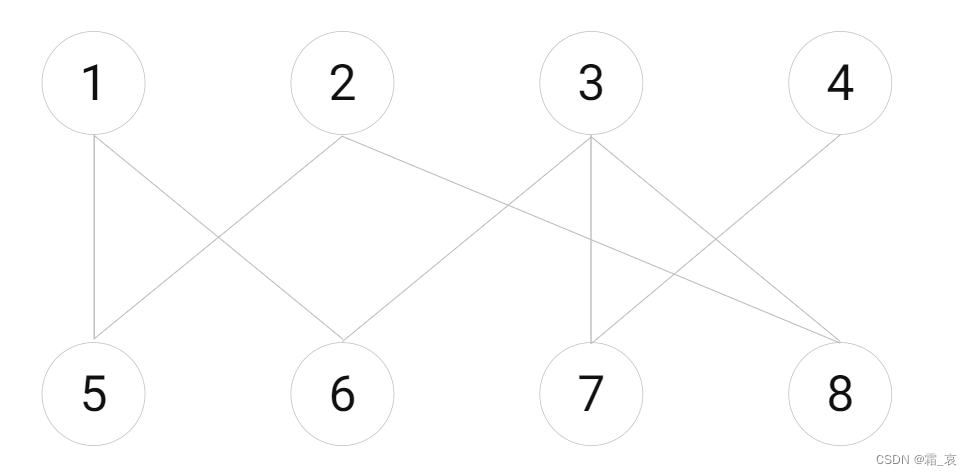
对于这个图，{x₁-x₅，x₂-x₈，x₃-x₆，x₄-x₇}是该图的一个匹配。注意，{x₁-x₅}也是该图的一个匹配。

如果一个匹配包括原图的所有点，那么这个匹配是一个完美匹配。
对于带权图来说，一个匹配的权重是匹配中所有边的权重之和。此时完美匹配需满足两个条件：包括所有点且该匹配拥有最小权重。我们也称此时的完美匹配为最小权重匹配。

应用：稳定婚烟问题

看下面的图，假定A,B是男生，C,D是女生。边的权重值越小，代表该男生、女生越喜欢ta的该相邻点：
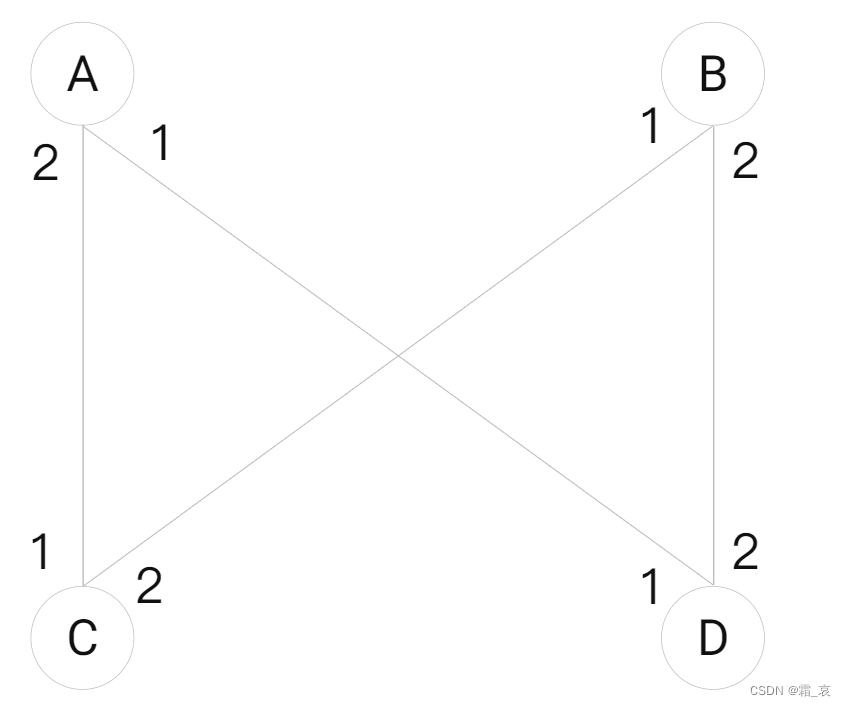
在这里插入图片描述

我们可以看出A更喜欢D，B更喜欢C…假定如果A和C结婚，B和D结婚，那么比起伴侣，A和D都更喜欢对方，那么他们可能发生出轨行为，导致婚烟不稳定。反之，如果A和D结婚，B和C结婚，那么婚烟是稳定的，因为即使C更喜欢A，但A更喜欢他的伴侣D，因此他不愿意和C出轨。
那么，对于一个带权图，怎么找到它的稳定婚烟匹配呢？

算法

首先明确一点：只有二分图才有稳定婚烟匹配，因此如果混入了gay或……那么不存在稳定婚烟匹配。另外，男女生数量必须相同，这点很好理解。我们可以通过一个称作TMA的算法找到一个图的一种稳定婚烟匹配。TMA步骤如下：

每个男生去找他最喜欢的女生示爱。
如果女生发现有多个男生来找她，她查看自己的权重并找到她最喜欢的，拒绝其他男生。注意这并不代表留下的这个男生就是她的最终伴侣。
被拒绝的男生将这个女生从他的权重名单里划掉，然后顺位去找下一个女生示爱。
重复第二步和第三步，直到每个女生面前有且只有一位男生示爱，算法结束，找到稳定婚烟匹配。

举个例子说明。假定对于每个男生和女生，他们的权重名单如下（这里跳过图阶段而直接抽象出信息），最左边的是最喜欢的，最右边的是最不喜欢的：
在这里插入图片描述

男生按照权重名单去找相对应的女生。
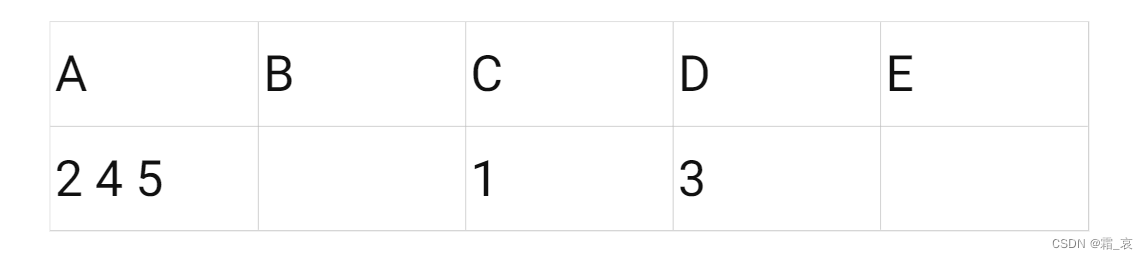
在A面前有三个男生，根据名单，她留下5；剩下的2 4两男生划掉A，分别去找下一个女生：
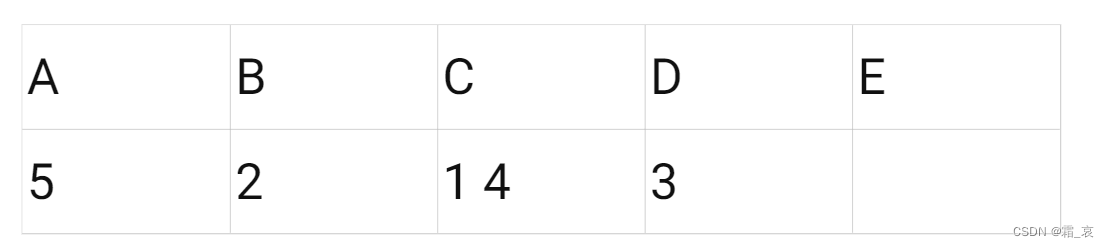
C查看名单，留下4；1划掉C，去找B：
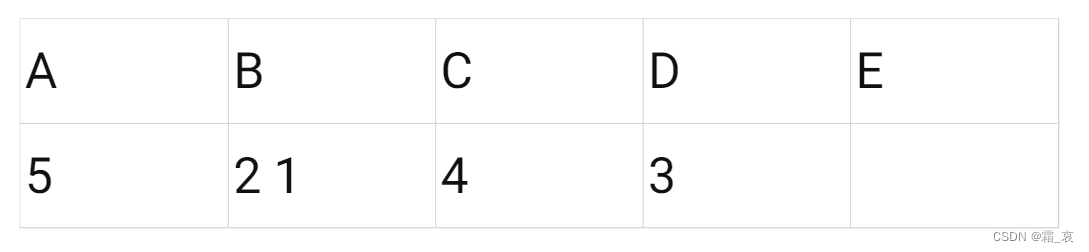
B查看名单，留下2；1划掉B，去找E：

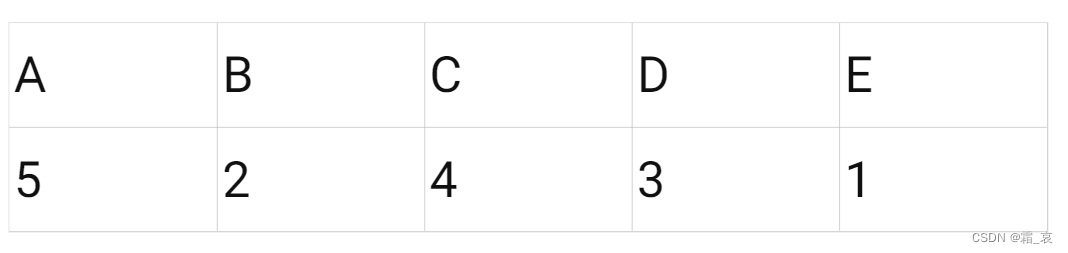
至此，所有女生面前有且仅有一个男生，算法结束。
经过检验（感兴趣的读者可以自行尝试一下），这个算法是有效的。接下来我们对其性质进行证明。

性质及其证明

性质1：这个算法会在不多于（n²+1）个周期内结束。这个性质很好理解，n个男生，n个女生，男生的名单最多划n²次，除了第一个回合外，每个回合至少有一个男生的名单会被划，因此算法最多执行（n²+1）个周期。
性质2：如果一个女生拒绝了一个男生，那么从她拒绝的那一天开始到算法结束，她身边一定有一个她更喜欢的示爱者。这个性质可以用归纳法来形式化的证明，但直观上也很好理解，假若女孩A拒绝男孩3在某一天，那么当天她留下的那个一定是更喜欢的，未来的某一天她即使拒绝了之前留下的，也说明有更更喜欢的示爱者来了，根据传递性，该性质正确。
性质3：每个人经过该算法的匹配后都有一个伴侣，这点不需证明。
性质4：TMA产生一个稳定婚烟匹配。如果一个男生和女生没能结婚，那么有两种可能：女生拒绝了男生，根据性质2，女生一定更喜欢现在的伴侣，不会产生出轨；男生没来找过女生，此时男生一定更喜欢他现在的伴侣，因此也不会产生出轨。
性质5（证明较复杂，参考知乎文章：稳定婚烟问题）：TMA算法中男生能找到保证稳定婚烟下的最佳情侣。用算法进行的轮数来归纳证明：

首先定义：如果A和B是合适的，那么存在一种稳定婚烟匹配中A和B配对。
基础步骤：利用归谬法证明在第1轮结束时，没有男生被合适的女生拒绝，即如果一个男生被女生拒绝，那么他们一定是不合适的。设女生A在第1轮拒绝1而选择了2，那么假设在某一个稳定匹配中，A和1结婚，那么A更喜欢2，而2最喜欢A，所以会发生出轨，则这个婚烟是不稳定的，出现矛盾，假设不成立，证明完成。
归纳步骤：如果在第n轮结束时，依然没有男生被合适的女生拒绝，则证明在（n+1）轮时依然不会有。设在第（n+1）轮，女生A拒绝1而选择了2，假设A和1在某个稳定匹配中结婚，那么A更喜欢2，对2来说，在TMA算法中拒绝他的女生都是不合适的，即不可能在任何稳定匹配中出现2与她们结婚的情况，因此在假想的稳定匹配中，他的最终伴侣一定差于A，那么2也更喜欢A，所以发生出轨，出现矛盾。因此一旦女生对男生合适，那么她就不会拒绝这个男生，又因为男生是按照他的喜好顺序求爱的，因此最后找到的一定是他的稳定最佳情侣。□

性质6：TMA算法中女生总会找到稳定最差情侣。依然用归谬法证明，假设存在一个稳定匹配，该匹配中有一个女生G匹配到比TMA匹配中更差的情侣B^’，那么她更喜欢在TMA算法中匹配到的男生B；对于B来说，由于性质5，他也一定更喜欢在TMA算法中匹配到的稳定最佳情侣G，所以出现出轨，产生矛盾，命题得证。□

我是霜_哀，在算法之路上努力前行的一位萌新，感谢你的阅读！如果觉得好的话，可以关注一下，我会在将来带来更多更全面的知识讲解！