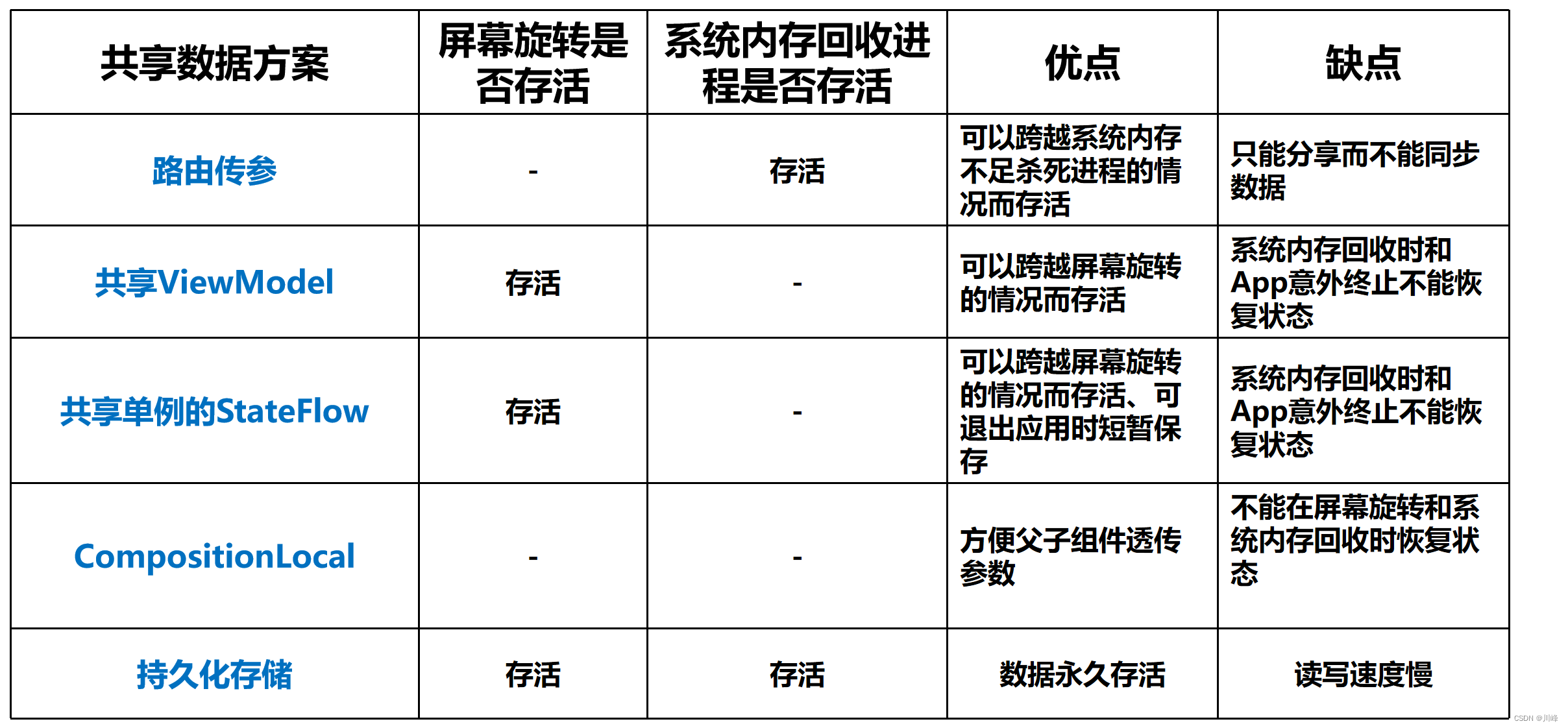
NLP学习笔记六-lstm模型
上一篇我们讲的是simple RNN模型,那么其实lstm模型更像是simple RNN模型的改进或者变种。
对于lstm模型,我们先看下面一张图:
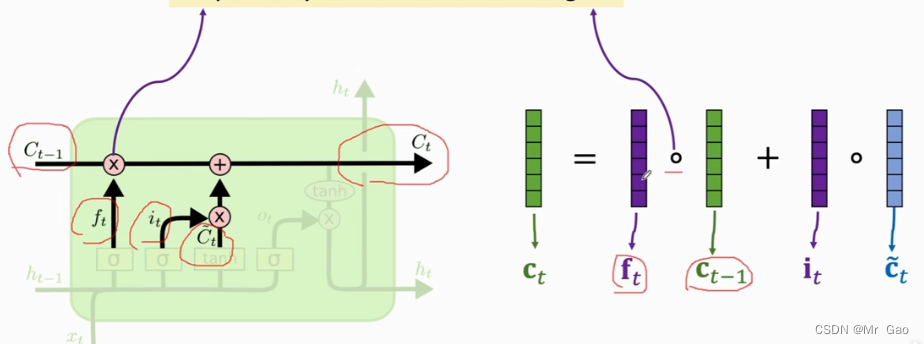
其实lstm模型的思想是建立在simple RNN模型上的,但是要更加贴近于显示,lstm模型认为,对于这种序列型的数据虽然simple RNN模型可以进行这种“信息记忆”,即simple RNN模型可以通过每次将上一个单元的输出利用起来,即当前单元的输出会考虑之前的输出。但是,他认为之前的有些信息是不需要的,所以加入了遗忘门,同时也认为当前输入x与上一个状态 h t h_t ht经过参数矩阵提取之后有些信息也是不需要的,所以又加入了输入门。
这里大家看一下上面的公式
f
t
f_t
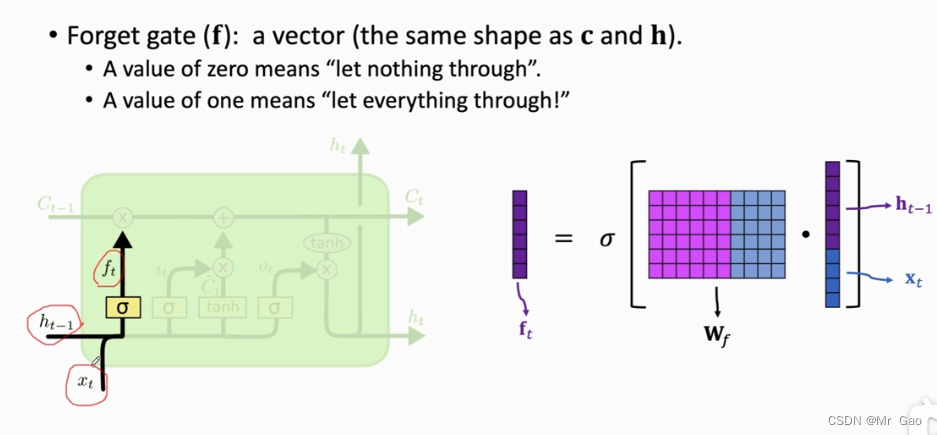
ft就是遗忘向量,它乘以上一个状态的输出就是对上一个状态的输出进行遗忘,有些信息就不要了,有些信息保存下来,所以
f
t
f_t
ft在得到之前得到了一个sigmoid函数的处理,使得
f
t
f_t
ft的值都在0-1之间,0-1即使
c
t
−
1
c_{t-1}
ct−1的遗忘程度。
那么
i
t
i_t
it就是输入向量,
c
t
/
c^{/}_t
ct/就是当前单元的输出,
c
t
/
c^{/}_t
ct/就是对应simple RNN的
h
t
h_t
ht。所以lstm模型它呢其实更加的注重之前信息的重要性相比较simple RNN模型。因为它无论遗忘向量
f
t
f_t
ft还是输入向量
i
t
i_t
it,还是
c
t
/
c^{/}_t
ct/都是由前一个单元的输出和当前单元输入拼接组成的向量乘以参数矩阵得到的,在最后呢,
c
t
c_t
ct又是前一个单元输出和当前单元的输出加权组合而成,其实在这个过程当中,我们可以发现
c
t
−
1
c_{t-1}
ct−1相比x输入被利用到的程度更高。也就是,我们更加注重之前信息的一个处理。
下面是遗忘向量的得到过程:
下面是输入向量的得到过程:
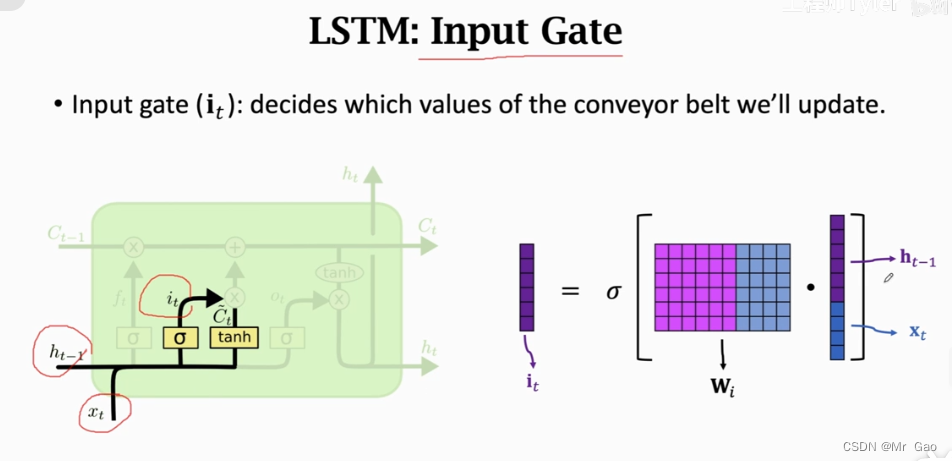
其实输入向量和遗忘向量得到的方法是一样的哈。
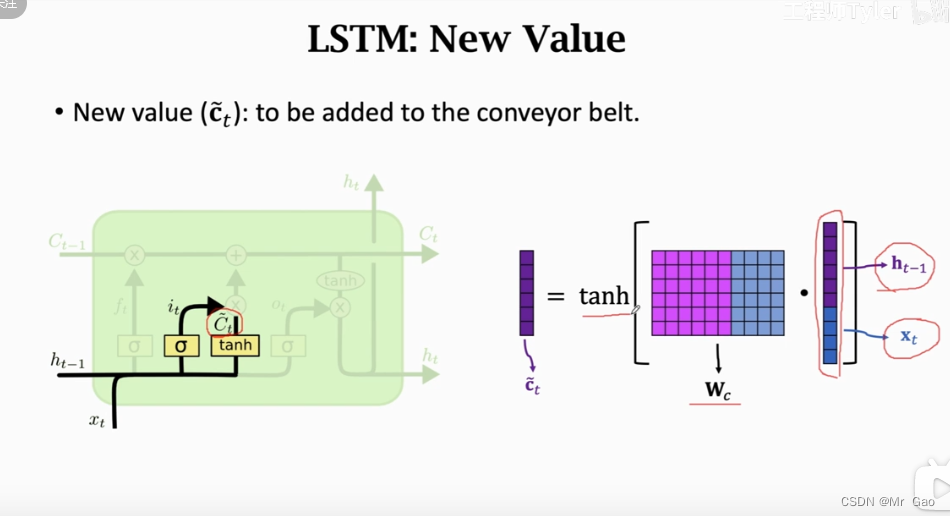
下面是当前单元new value的情况:
其实
c
t
/
c^{/}_t
ct/不是就RNN模型中的
h
t
h_t
ht吗?
哈哈哈,如果你理解了c^{/}_t
和
R
N
N
模型中的
和RNN模型中的
和RNN模型中的h_t$的关系其实会帮助你理解lstm模型。
最后我们还需要一个输出门,也就是对于当前转
c
t
c_t
ct再进行一次限制转换,其实博主觉得,lstm模型看起来过于冗余,它一次又一次的对数据进行遗忘或者进行限制。先是对上一个状态的
c
t
−
1
c_{t-1}
ct−1进行一次遗忘门处理,然后又再次对
c
t
/
c^{/}_t
ct/进行了一次输入门处理,其实说是输入门处理,实际上也是遗忘门处理,这里大家看懂的话会理解的,最后又对
c
t
/
c^{/}_t
ct/和
c
t
−
1
c_{t-1}
ct−1的加权结果有进行一次输出门处理,其实这个输出们处理也是遗忘门处理。
当然这要多亏了BP反向传播算法,否则这些想法都只是猜想。
下面是输出门的实现过程:
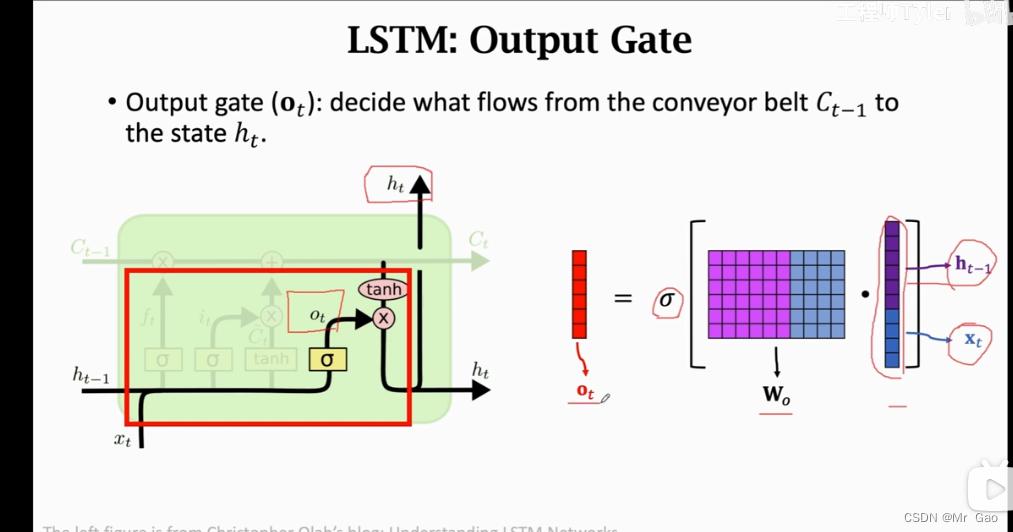
现在我们再来看看lstm,模型,我们可以发现,其实lstm模型,加入了很多限制,也就是它其实并没有去增强信息,而是不断地在遗忘信息,输入门、遗忘门、输出门起到的其实都是遗忘作用,另外lstm模型输入门、遗忘门、输出门的遗忘效果都是由上一个单元的输出和当前单元的输入共同决定的。然后,利用上一个单元的
c
t
−
1
c_{t-1}
ct−1和当前单元的
c
t
/
c^{/}_t
ct/加权组成当前单元主要的信息向量。也就是说是否进行遗忘,在lstm模型中,更加取决于,上一个状态的输出
h
t
h_t
ht和当前状态的输入x。然后再次基础上考虑上一个单元的
c
t
−
1
c_{t-1}
ct−1和当前单元的
c
t
/
c^{/}_t
ct/经过输入门,遗忘门处理之后的加权结果。
我认为其实lstm模型是有问题的:
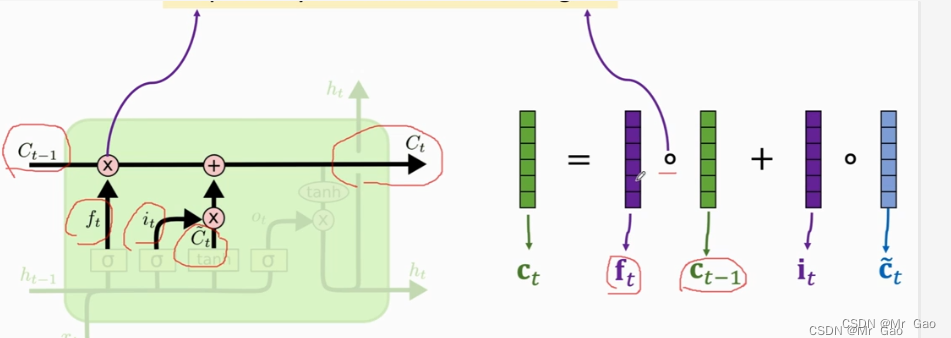
看下面一张图,
c
t
c_t
ct的遗忘由上一个状态的输出
h
t
h_t
ht和当前状态的输入x决定,而
c
t
−
1
c_{t-1}
ct−1也由上一个状态的输出
h
t
h_t
ht和当前状态的输入x决定,但是我们知道
c
t
−
1
c_{t-1}
ct−1是由上一个状态的输出
h
t
h_t
ht和当前状态的输入x得到的,自己得到自己,再对自己进行遗忘,这有没有问题。然后
f
t
f_t
ft确是由上一个状态的输出
h
t
h_t
ht和当前状态的输入x得到的,但
c
t
c_t
ct只是由之前状态决定的,也就是由由上一个状态的输出
h
t
h_t
ht和当前状态的输入x决定之前信息的遗忘,其实对于信息的遗忘,我认为lstm模型或许还有待完善的地方,或许,我们的遗忘策略可以更加完善。当前信息遗忘可以由之前信息和当前输入共同决定,之前信息的遗忘也由之前信息和当前输入共同决定,而不是自己决定自己的遗忘。

![[Python图像处理] 基于离散余弦变换的安全扩频数字水印](https://img-blog.csdnimg.cn/4e9777ab479b46a2b6ee5393b5a78be8.png#pic_center)