欢迎访问个人网络日志🌹🌹知行空间🌹🌹
文章目录
- 0.关于卡尔曼
- 1.卡尔曼滤波算法
- 2.卡尔曼滤波算法的应用
- 一个简单例子
- 一个复杂的例子
- 参考
0.关于卡尔曼
卡尔曼,匈牙利数学家,1930年出生于匈牙利首都布达佩斯。1953,1954,1957年分别于麻省理工学院分别获得电机工程学士及硕士学位。于哥伦比亚大学获得博士学位。卡尔曼滤波器正是源于他的博士论文和1960年发表的论文《A New Approach to Linear Filtering and Prediction Problems》。
卡尔曼滤波器是求解线性高斯系统状态估计的最优化自回归数据处理算法,其广泛应用在机器人导航,控制,传感器数据融合甚至在军事方面的雷达系统以及导弹追踪等。
1.卡尔曼滤波算法
卡尔曼算法可用于线性高斯系统的最优状态估计,线性高斯系统是指其系统方程是线性的,满足比例性和可加性,系统噪声服从高斯分布。
对于一个线性控制系统,我们可以得到系统状态变量的运动方程,及状态变量值的观测方程,使用如下方程表示,
{ x k = A k x k − 1 + B k μ k + ω k z k = H k x k + v k k = 1 , . . . , N \left\{\begin{matrix} x_k=A_kx_{k-1}+B_k\mu_k+\omega_k\\ z_k=H_kx_k+v_k \end{matrix}\right. \space k=1,...,N {xk=Akxk−1+Bkμk+ωkzk=Hkxk+vk k=1,...,N
- k k k表示的第 k k k时刻
- x k x_k xk表示的是 k k k时刻的系统状态量,根据运动方程来预测
- A A A是状态转移矩阵,从 k − 1 k-1 k−1时刻的 x k − 1 x_{k-1} xk−1到 k k k时刻的 x k x_k xk
- μ k \mu_k μk是 k k k时刻系统输入的控制变量
- B B B是从控制变量映射到状态变量的矩阵
- ω k ∼ N ( 0 , Q ) \omega_k\sim N(0, Q) ωk∼N(0,Q)表示的是状态的噪声,对于高斯系统,噪声服从正态分布
- Q Q Q是状态噪声的方差
- H H H是从状态变量到观测变量的映射矩阵
- v k ∼ N ( 0 , R ) v_k\sim N(0, R) vk∼N(0,R)表示的测量值,观测变量的噪声,对于高斯系统,噪声服从正态分布
- R R R是测量噪声的方差
对于实际中的控制系统,系统状态的值有三个,一个是系统运行的真实值,这个是没有办法获得的,因为无论是测量得到的观测值,还是根据状态转移方程即运动方程计算得到的预测值,都存在误差。最好的办法就是,能够根据预测值和测量值的可信度,自动的平衡取测量值和预测值中间的某个值作为系统状态的估计值。这正是卡尔曼滤波器发挥作用的地方。
直接给出卡尔曼滤波最关键的五个方程,
预测方程(运动方程):
{ x k ∣ k − 1 = A k x k − 1 ∣ k − 1 + B k μ k P k ∣ k − 1 = A k P k − 1 ∣ k − 1 A + k T + Q k \left\{\begin{matrix} x_{k|k-1}=A_kx_{k-1|k-1}+B_k\mu_k\\ P_{k|k-1}=A_kP_{k-1|k-1}A+k^T+Q_k \end{matrix}\right. {xk∣k−1=Akxk−1∣k−1+BkμkPk∣k−1=AkPk−1∣k−1A+kT+Qk
更新方程
{ K k = P k ∣ k − 1 H k T ( H k P k ∣ k − 1 H k T + R k ) − 1 x k ∣ k = x k ∣ k − 1 + K k ( z k − H k x k ∣ k − 1 ) P k ∣ k = ( I − K k H k ) P k ∣ k − 1 \left\{\begin{matrix} K_k=P_{k|k-1}H_k^T(H_kP_{k|k-1}H_k^T+R_k)^{-1}\\ x_{k|k}=x_{k|k-1}+K_k(z_k-H_kx_{k|k-1})\\ P_{k|k}=(I-K_kH_k)P_{k|k-1} \end{matrix}\right. ⎩ ⎨ ⎧Kk=Pk∣k−1HkT(HkPk∣k−1HkT+Rk)−1xk∣k=xk∣k−1+Kk(zk−Hkxk∣k−1)Pk∣k=(I−KkHk)Pk∣k−1
- x k ∣ k − 1 x_{k|k-1} xk∣k−1表示从 k − 1 k-1 k−1时刻到 k k k时刻,状态转移得到预测值
- x k ∣ k x_{k|k} xk∣k是使用卡尔曼滤波后综合预测值和观测值后得到的估计值
- P P P是状态变量的协方差矩阵
- K k K_k Kk是卡尔曼增益,仔细观察其形如 E r r o r p r e d i c t i o n E r r o r p r e d i c t i o n + E r r o r o b e r v a t i o n \frac{Error_{prediction}}{Error_{prediction}+Error_{obervation}} Errorprediction+ErrorobervationErrorprediction,因此卡尔曼增益平衡了预测值和测量值的误差。
- I I I表示的是单位矩阵。
到这里,卡尔曼滤波算法的原理部分就介绍完毕了,接下来部分,使用一个具体的例子来介绍卡尔曼滤波的应用。
2.卡尔曼滤波算法的应用
一个简单例子
估计水箱中的水的量,水箱是水平的,水箱中水的体积也是近似固定的,即一个静态的系统。
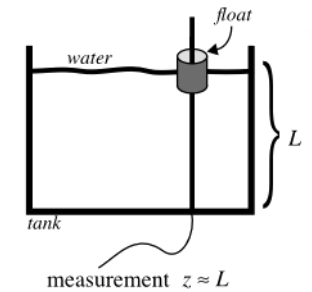
水箱的真实水量 L = c L=c L=c
系统状态变量只剩下一维: x ^ = x \hat{x} =x x^=x, x x x是水的体积 L L L的估计量
因为水箱中的水的体积假设是不变,因此 x k + 1 = x k x_{k+1}=x_k xk+1=xk, A = 1 , B = 0 A=1,B=0 A=1,B=0
水箱的测量量是浮子的数值,有可能浮子(float)的数值是 1 c m 1cm 1cm对应水的体积是 1 1 1升,为简化系统,假设测量量 z = x , 即 H = 1 z=x,即H=1 z=x,即H=1
测量值的噪声假设 R = r R=r R=r
状态量只有一维,其协方差矩阵中只有一个数, P = p P=p P=p,假设状态量的预测值的噪声 Q = q Q=q Q=q
基于上面的假设,用于这个简单水箱系统水深估计的卡尔曼滤波方程表示为:
预测方程
{ x k ∣ k − 1 = x k − 1 ∣ k − 1 p k ∣ k − 1 = p k − 1 ∣ k − 1 + q \left\{\begin{matrix} x_{k|k-1}=x_{k-1|k-1} \\ p_{k|k-1}=p_{k-1|k-1}+q \end{matrix}\right. {xk∣k−1=xk−1∣k−1pk∣k−1=pk−1∣k−1+q
更新方程
{ K k = p k ∣ k − 1 ( p k ∣ k − 1 + r ) − 1 x k ∣ k = x k ∣ k − 1 + K k ( z k − x k ∣ k − 1 ) p k ∣ k = ( 1 − K k ) p k ∣ k − 1 \left\{\begin{matrix} K_k=p_{k|k-1}(p_{k|k-1}+r)^{-1}\\ x_{k|k}=x_{k|k-1} + K_{k}(z_k-x_{k|k-1}) \\ p_{k|k}=(1-K_k)p_{k|k-1} \end{matrix}\right. ⎩ ⎨ ⎧Kk=pk∣k−1(pk∣k−1+r)−1xk∣k=xk∣k−1+Kk(zk−xk∣k−1)pk∣k=(1−Kk)pk∣k−1
基于上面的假设,这个非常简单的水箱模型就定义完了,现在代入一些值来看一下计算过程:
状态初始化
假设水箱中水的实际体积是 1 1 1升,初始估计的水的体积是 x 0 = 0 x_0=0 x0=0,因为初始值是随机设置的,因此开始时系统状态预测量的方差很大, p 0 = 1000 p_0=1000 p0=1000。水箱中的水实际上没有变化,因此状态量的预测噪声应该很小,假设 q = 0.0001 q=0.0001 q=0.0001。测量的噪声假设为 r = 0.1 r=0.1 r=0.1。
- 第1步
- 预测, 假设测量值 z 1 = 0.9 z_1=0.9 z1=0.9
- { x 1 ∣ 0 = 0 p 1 ∣ 0 = 1000 + 0.0001 \left\{\begin{matrix} x_{1|0}=0\\ p_{1|0}=1000+0.0001 \end{matrix}\right. {x1∣0=0p1∣0=1000+0.0001
- 更新
- { K 1 = ( 1000 + 0.0001 ) [ ( 1000 + 0.0001 ) + 0.1 ] − 1 ≈ 0.9999 x 1 ∣ 1 = 0 + 0.9999 ( 0.9 − 0 ) = 0.8999 p 1 ∣ 1 = ( 1 − 0.9999 ) ( 1000 + 0.0001 ) ≈ 0.1 \left\{\begin{matrix} K_1=(1000+0.0001)[(1000+0.0001)+0.1]^{-1}\approx0.9999\\ x_{1|1}=0+0.9999(0.9-0)=0.8999\\ p_{1|1}=(1-0.9999)(1000+0.0001)\approx 0.1 \end{matrix}\right. ⎩ ⎨ ⎧K1=(1000+0.0001)[(1000+0.0001)+0.1]−1≈0.9999x1∣1=0+0.9999(0.9−0)=0.8999p1∣1=(1−0.9999)(1000+0.0001)≈0.1
这样,经过一步迭代,可以发现状态量预测值的方差已经降到了 0.1 0.1 0.1,状态量的值已经从 0 → 0.8999 0\rightarrow0.8999 0→0.8999,已经比较接近真实值了。
继续后面的迭代,可得到如下的表格:
| k | x k ∣ k − 1 x_{k|k-1} xk∣k−1 | p k ∣ k − 1 p_{k|k-1} pk∣k−1 | z k z_k zk | K k K_k Kk | x k ∣ k x_{k|k} xk∣k | p k ∣ k p_{k|k} pk∣k |
|---|---|---|---|---|---|---|
| 2 | 0.8999 | 0.1001 | 0.8 | 0.5002 | 0.8499 | 0.05 |
| 3 | 0.8499 | 0.0501 | 1.1 | 0.3339 | 0.9334 | 0.0334 |
| 4 | 0.9334 | 0.0335 | 1.0 | 0.2509 | 0.9501 | 0.0251 |
| 5 | 0.9501 | 0.0252 | 0.95 | 0.2012 | 0.9501 | 0.0201 |
| 6 | 0.9501 | 0.0202 | 1.05 | 0.1682 | 0.9669 | 0.0168 |
| 7 | 0.9669 | 0.0169 | 1.2 | 0.1447 | 1.0006 | 0.0145 |
| 8 | 1.0006 | 0.0146 | 0.9 | 0.1272 | 0.9878 | 0.0127 |
| 9 | 0.9878 | 0.0128 | 0.85 | 0.1136 | 0.9722 | 0.0114 |
| 10 | 0.9722 | 0.0115 | 1.15 | 0.1028 | 0.9905 | 0.0103 |
从上面表格中的可以看到,估计量 x x x越来越接近系统的真实值 1 1 1;
同时估计量的方差 p p p越来越小,说明估计量越来越稳定;
卡尔曼增益的值越来越小,还记得前面介绍的卡尔曼增益的含义是预测量误差在系统总误差中的占比,系统预测量越来越准,因此卡尔曼增益越来越小。
一个复杂的例子
上面介绍的是非常简单的一个系统,状态变量也只有一个,为了与实际应用更接近,看一个状态变量是多维度的例子,此时状态变量的协方差是一个矩阵,状态转移等也都是矩阵。
TODO
先鸽了,复杂例子后面再加吧^_^
欢迎访问个人网络日志🌹🌹知行空间🌹🌹
参考
简单例子部分参考自康奈尔大学的讲义,可以直接看讲义。
- 1.https://www.cs.cornell.edu/courses/cs4758/2012sp/materials/MI63slides.pdf
- 2.https://thekalmanfilter.com/kalman-filter-explained-simply/
- 3.https://towardsdatascience.com/kalman-filter-in-a-nutshell-e66154a06862