一、什么是最近公共祖先

LCA为最近公共祖先（Lowest Common Ancestor）的缩写。
对于一棵有根树T的两个节点u,v,最近公共祖先LCA(T,u,v)代表一个节点x。

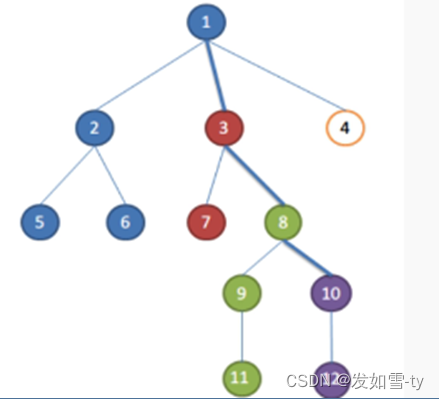
LCA(5,6) = 2
LCA(7,12) = 3
LCA(2,1)=1

二、公共祖先的朴素解法

1. 两个节点先调整到相同的深度
2. 每一次两个点同时向上跳一层，当两个点相遇即为所求两点的LCA.
   对于一组询问，时间复杂度为O(N)

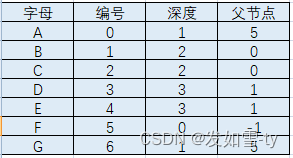
需要深度遍历，然后构造出这么一张表

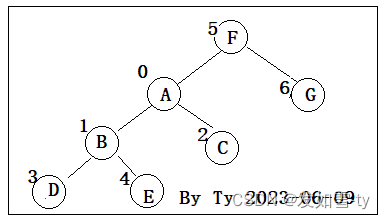
假设求LCA(D,G)
第一步：先判断D的深度为3，G的深度为1
第二步：将D根据父节点数组，往上走一步，也就是节点B，
第三步：此时深度B为2和1还是不同，需要继续往上，也就是A,此时 A,G的深度一致
第四步：判读A的父节点和G的父节点是否一致，如果一致则找到，不一致则同时上调一步，如此循环直到两者父节点首次相同。

三、递归解法

有以下图

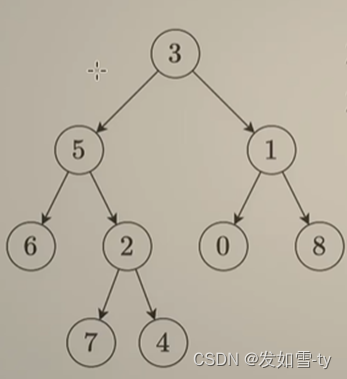
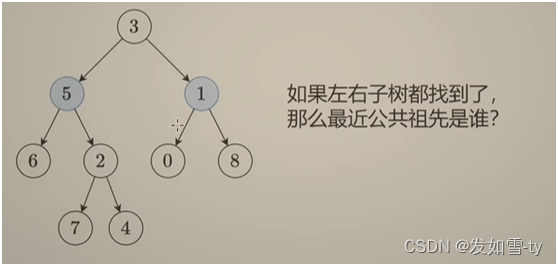
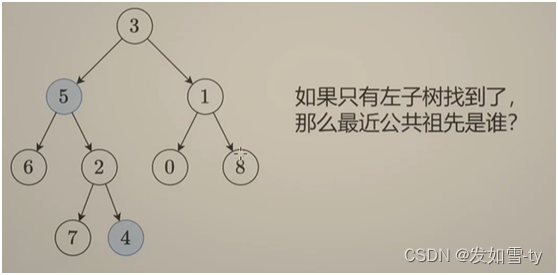
四、代码

以下代码，构建了如下的一颗树，并分别实现了朴素法和递归法

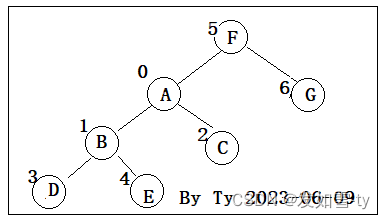
#include<iostream>
using namespace std;
using ElemType = char;

typedef struct BiTNode
{
	ElemType data;
	int nIndex;
	struct BiTNode* lchild;
	struct BiTNode* rchild;

}BiTNode, * BiTree;

int arrayD[100] = { -1 };
int arrayF[100] = { -1 };
void DFS(BiTNode* tree, int nd, int nf)
{
	if (tree)
	{
		DFS(tree->lchild, nd + 1, tree->nIndex);
		arrayD[tree->nIndex] = nd;
		arrayF[tree->nIndex] = nf;
		DFS(tree->rchild, nd + 1, tree->nIndex);
	}
}

int LCA1(int u, int v)
{
	if (arrayD[u] < arrayD[v])
	{
		swap(u, v);
	}

	if (arrayD[u] > arrayD[v] && arrayF[u] != v)
	{
		while (arrayD[u] != arrayD[v])
		{
			u = arrayF[u];
		}

		while (arrayF[u] != arrayF[v])
		{
			u = arrayF[u];
			v = arrayF[v];
		}

	}

	return arrayF[u];

}

BiTNode* LCA2(BiTNode *pRoot,BiTNode *p,BiTNode *q)
{
	if (pRoot == p|| pRoot == q || pRoot == NULL)
	{
		return pRoot;
	}

	BiTNode* pLeft = LCA2(pRoot->lchild, p, q);
	BiTNode* pRight = LCA2(pRoot->rchild, p, q);

	if (pLeft && pRight)
	{
		return pRoot;
	}
	else if (pLeft)
	{
		return pLeft;
	}
	else if (pRight)
	{
		return pRight;
	}
	else
	{
		return NULL;
	}
}

int main()
{

	BiTNode b1, b2, b3, b4, b5, b6, b7;
	memset(&b1, 0, sizeof(BiTNode));
	memset(&b2, 0, sizeof(BiTNode));
	memset(&b3, 0, sizeof(BiTNode));
	memset(&b4, 0, sizeof(BiTNode));
	memset(&b5, 0, sizeof(BiTNode));
	memset(&b6, 0, sizeof(BiTNode));
	memset(&b7, 0, sizeof(BiTNode));

	b1.nIndex = 0; b1.data = 'A';
	b2.nIndex = 1; b2.data = 'B';
	b3.nIndex = 2; b3.data = 'C';
	b4.nIndex = 3; b4.data = 'D';
	b5.nIndex = 4; b5.data = 'E';
	b6.nIndex = 5; b6.data = 'F';
	b7.nIndex = 6; b7.data = 'G';
	//构建树关系
	b1.lchild = &b2;
	b1.rchild = &b3;
	b2.lchild = &b4;
	b2.rchild = &b5;

//根
b6.lchild = &b1;
b6.rchild = &b7;


cout << "LCA1:\n";
	DFS(&b6, 0, -1);

	int nIndex = LCA1(b1.nIndex, b2.nIndex);
	if (nIndex >= 0)
	{
		printf("LCA(%c,%c)= index(%d)\n", b1.data, b2.data, nIndex);
	}

	nIndex = LCA1(b5.nIndex, b7.nIndex);
	if (nIndex >= 0)
	{
		printf("LCA(%c,%c)= index(%d)\n", b5.data, b7.data, nIndex);
	}
	
	//LCA2
	cout << "LCA2:\n";

	BiTNode *pLCA = LCA2(&b6, &b1, &b2);
	if (pLCA)
	{
		printf("LCA(%c,%c)= %c\n",b1.data,b2.data, pLCA->data);
	}

	pLCA = LCA2(&b6, &b5, &b7);
	if (pLCA)
	{
		printf("LCA(%c,%c)= %c\n", b5.data, b7.data, pLCA->data);
	}
	system("pause");
}