一文读懂二叉树

news2025/1/21 2:49:33

大家好，我是三叔，很高兴这期又和大家见面了，一个奋斗在互联网的打工人。

什么是二叉树

二叉树是一种由节点（Node）组成的数据结构，每个节点最多有两个子节点。它具有良好的层次结构，便于搜索和遍历。二叉树的定义和操作方法可以通过面向对象的方式来理解，每个节点都是一个对象，节点之间通过引用关系连接。

常见的二叉树有哪些

满二叉树
完全二叉树

什么是满二叉树

如图所示：

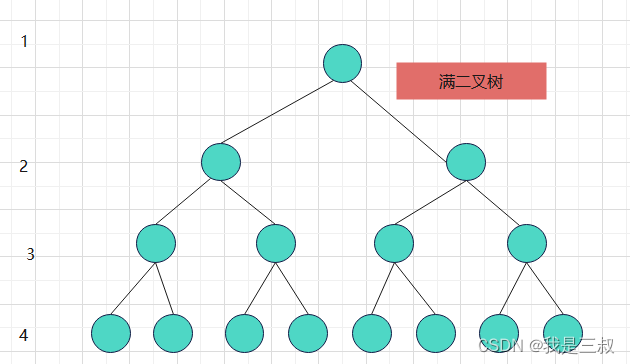
在这里插入图片描述
这棵二叉树为满二叉树，也可以说深度为k，有2^k-1个节点的二叉树。根节点为 k = 1 的深度开始计算，如图所示的二叉树，它的深度为 4 ，所以这棵满二叉树有15个节点。

什么是完全二叉树

完全二叉树中，除了最底层节点以外，其余每层节点数都达到最大值，并且最下面一层的节点从左到右是连续的，这样的二叉树为完全二叉树。

如图1所示：最底部的节点数从左至右是连续的，该树为完全二叉树

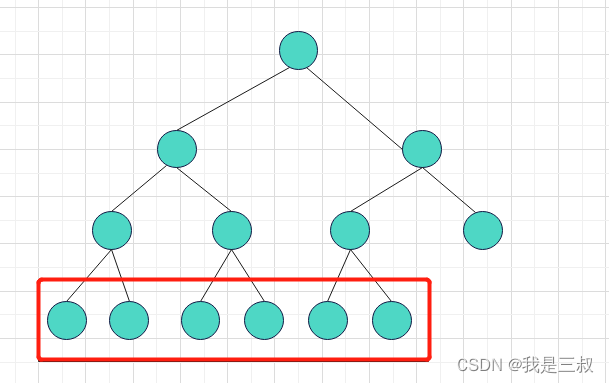
在这里插入图片描述
如图2所示：从左至右是连续的，因此也是完全二叉树

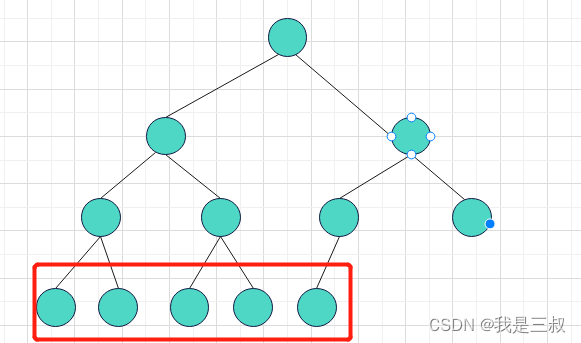
在这里插入图片描述

如图3所示：最底部的节点不是连续的，该树不是一个完全二叉树

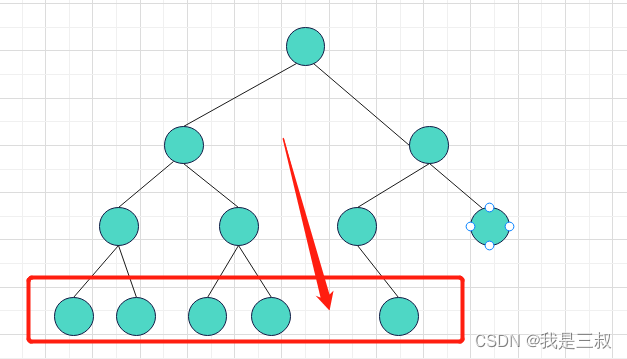
在这里插入图片描述

什么是二叉搜索树

前面介绍的树，都没有数值的，而二叉搜索树是有数值的了，二叉搜索树是一个有序树。

若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
它的左、右子树也分别为二叉排序树

如图所示：这棵树就是一颗二叉搜索树

在这里插入图片描述

什么是平衡二叉搜索树

平衡二叉搜索树：又被称为AVL（Adelson-Velsky and Landis）树，且具有以下性质：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。

它通过在插入和删除节点时进行旋转操作来保持树的平衡。AVL树的平衡因子（左子树高度减去右子树高度的差值）在范围[-1, 1]之间。

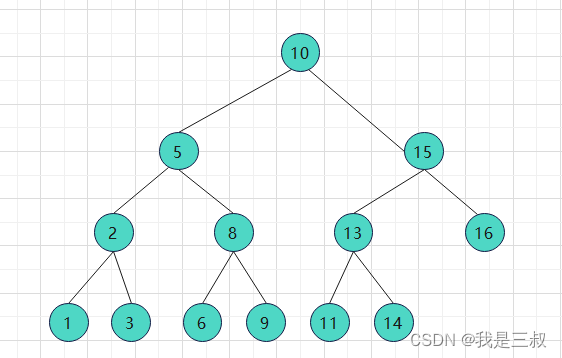
如图所示：这是一颗平衡二叉树，它的左右两个树的高度差在为1

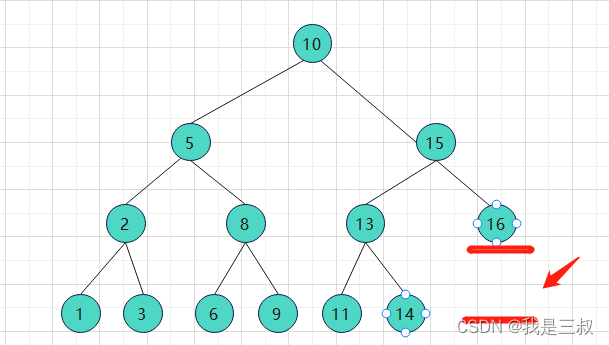
在这里插入图片描述

如图所示：它的高度差为1，因此也是一个平衡二叉搜索树

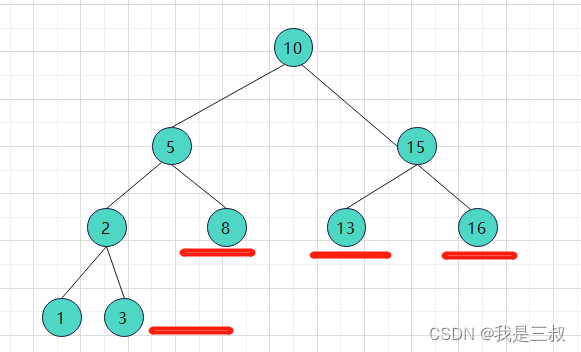
在这里插入图片描述

如图所示：它的高度差已经大于1了，这不是一棵平衡二叉搜索树

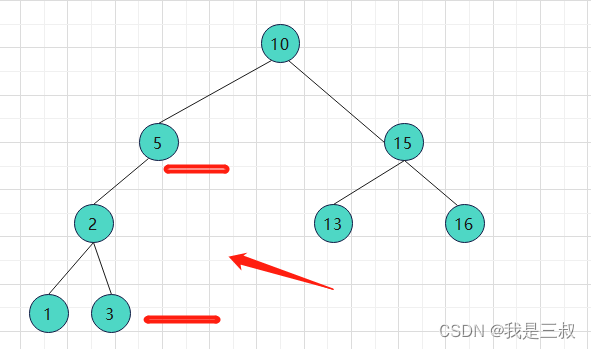
在这里插入图片描述

二叉搜索树的存储方式

二叉搜索树的存储方式主要有两种：链式存储和数组存储。

链式存储：
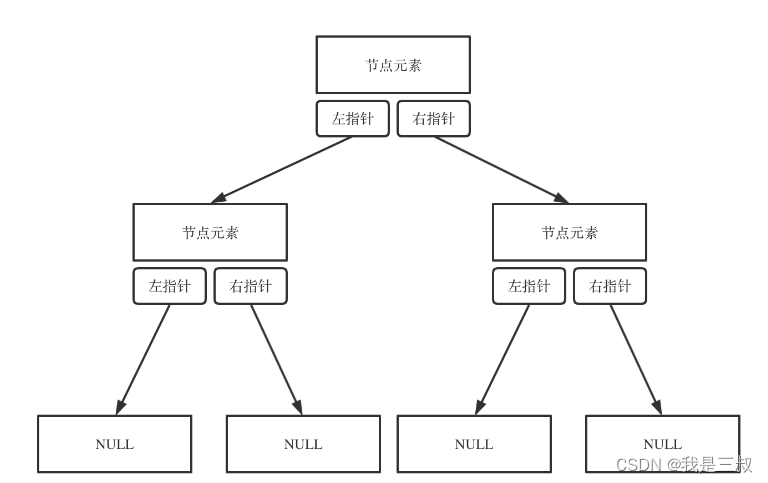
在链式存储方式中，每个节点由一个对象（或结构体）表示，并包含指向其左子节点和右子节点的指针（或引用）。每个节点的结构可以包含一个键（用于比较和排序）以及其他相关数据。
优点：
灵活性：链式存储方式可以动态地分配内存，并且可以根据需要插入、删除节点，使得树的结构可以动态变化。
插入和删除效率高：由于节点的指针连接，插入和删除操作只需要改变指针的指向，效率较高。
缺点：
需要额外的指针空间：每个节点需要存储左子节点和右子节点的指针，占用额外的空间。
指针操作可能增加内存开销：在大规模数据集的情况下，节点对象和指针操作可能导致额外的内存开销。

如图所示：链式存储

在这里插入图片描述

数组存储：
在数组存储方式中，使用一个数组来表示二叉搜索树的结构。数组的索引位置对应着节点的顺序，节点的值存储在数组中的对应位置。
优点：
内存连续：数组存储方式使用连续的内存空间，可以减少指针操作的开销。
访问效率高：通过数组的索引可以直接访问节点，查找效率较高。
缺点：
静态结构：数组存储方式需要预先确定数组的大小，无法动态调整树的结构，因此不适用于频繁的插入和删除操作。
内存空间浪费：如果树的大小不确定，可能会浪费一部分数组空间。

如图所示：数组存储

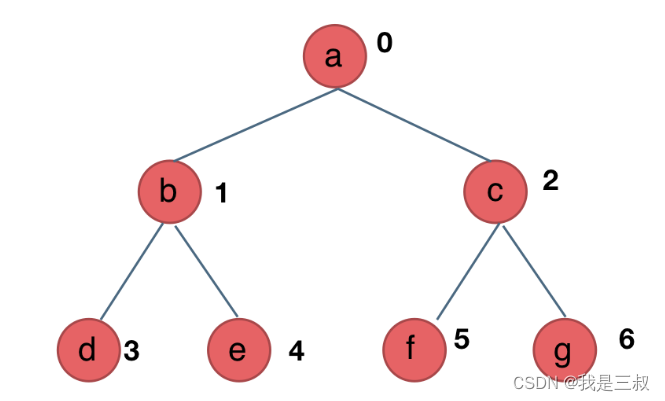
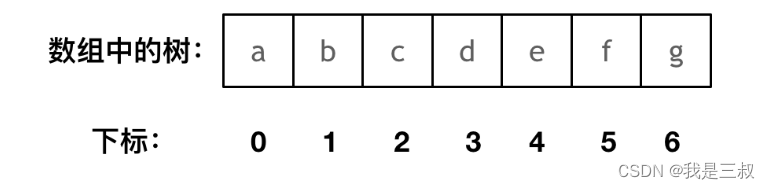
在这里插入图片描述
如果父节点的数组下标是 i，那么它的左孩子就是 i * 2 + 1，右孩子就是 i * 2 + 2。

但是用链式表示的二叉树，更有利于我们理解，所以一般我们都是用链式存储二叉树。

二叉树的遍历

二叉树主要有两种遍历方式：

深度优先遍历：先往深走，遇到叶子节点再往回走，一条路走到黑，走到最低部再回退回来。
前序遍历（递归法，迭代法）
中序遍历（递归法，迭代法）
后序遍历（递归法，迭代法）
广度优先遍历：一层一层的去遍历。
层次遍历（迭代法）

什么是前序遍历

前序遍历就是从根节点开始，先遍历中间节点，在遍历左节点（同时左节点又分为中-》左-》右），最后遍历右节点（同时右节点又分为中-》左-》右）

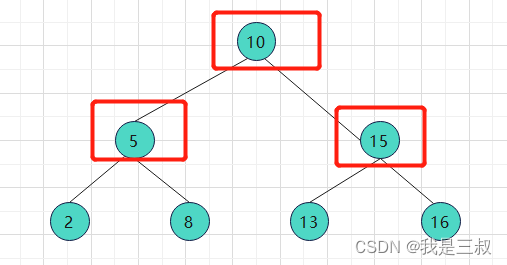
如图所示：
这棵树前序遍历的结果是：10 5 2 8 15 13 16

在这里插入图片描述

什么是中序遍历

同理，中序遍历就是先遍历左节点（同时左节点分为左中右），再遍历中节点，最后遍历右节点（右节点也按照左中右来遍历）

如上图所示：
中序遍历结果是：2 5 8 10 13 15 16

什么是后续遍历

同理，后续遍历就是先遍历左节点（同时左节点分为左右中），再遍历右节点（右节点也按照左右中国来遍历），最后处理中间节点

如上图所示：
后续遍历结果是：2 8 5 13 16 15 10

通过上面的遍历结果其实可以了解到，前中后序遍历对应的中间节点的位置分别为前中后，所以前中后序遍历代表着中间节点所对应的位置。

手写一个二叉搜索树

不废话，上代码：

public class TreeNode {
    int val; // 数值

    TreeNode left; // 左指针,指向左孩子

    TreeNode right; // 右指针，指向右孩子

    public TreeNode() {

    }

    public TreeNode(int val) {
        this.val = val;
    }

    public TreeNode(int val, TreeNode left, TreeNode right) {
        this.val = val;
        this.left = left;
        this.right = right;
    }
}