【算法题解】35. 两两交换链表中的节点

news2024/11/23 1:40:03

这是一道 中等难度 的题

https://leetcode.cn/problems/swap-nodes-in-pairs/

题目

给你一个链表，两两交换其中相邻的节点，并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题（即，只能进行节点交换）。

示例 1：

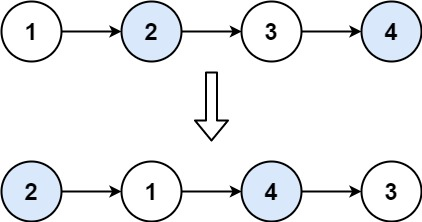
输入：head = [1,2,3,4]
输出：[2,1,4,3]

示例 2：

输入：head = []
输出：[]

示例 3：

输入：head = [1]
输出：[1]

提示：

链表中节点的数目在范围 $[0, 100]$ 内
$0 <= N o d e . v a l <= 100$

递归解法

假如除了前面的两个节点，后面的已经两两交换过了，且结果为 swapPairs(head.next.next)。

那么我们只需要交换前两个节点即可，以 head = [1,2,3,4,5,6,7] 为例：

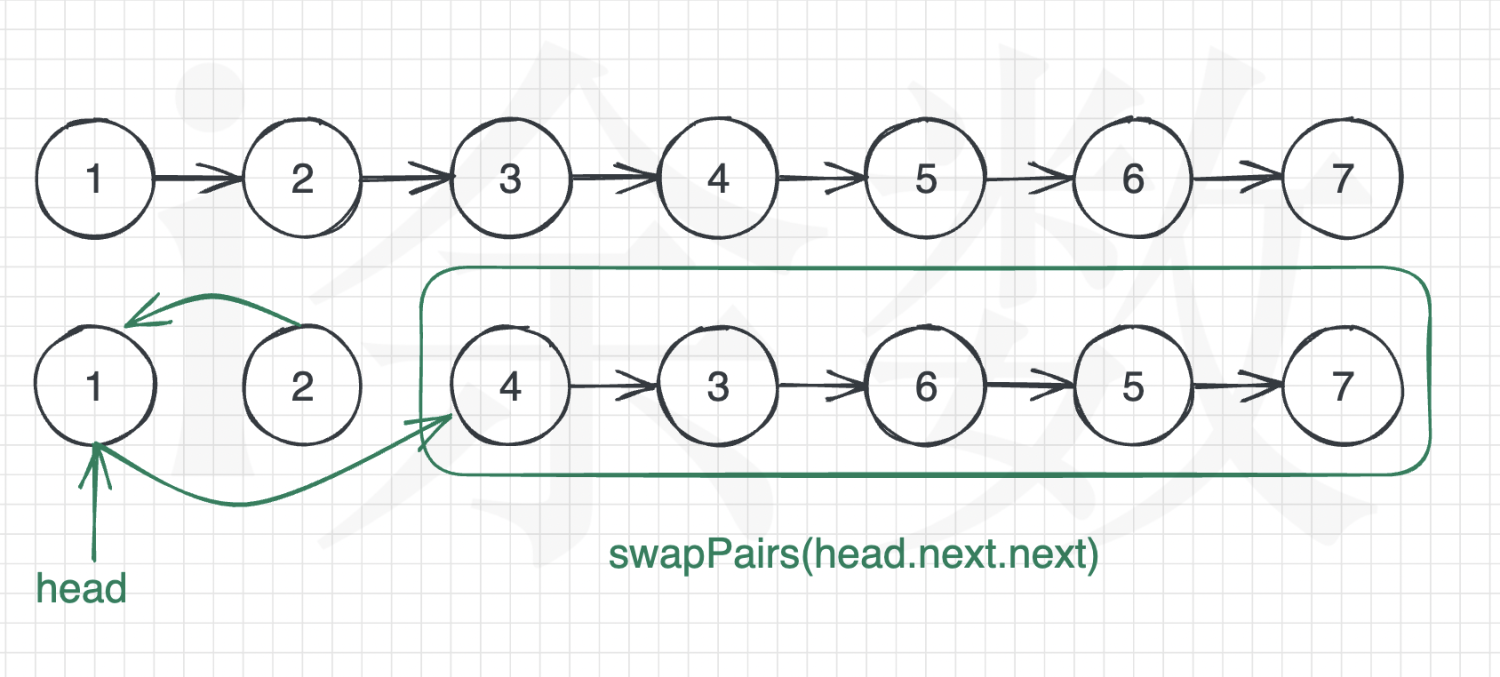
同理，后续链表也认为只需要交换前两个节点，head.next.next 已经交换完毕。逐层调用即为递归。

以Java代码为例，递归函数为：

ListNode next = head.next;
ListNode nextHead = next.next;

// 交换
next.next = head;
head.next = swapPairs(nextHead);

边界条件：head为空或者head.next为空，即后续节点个数不够两个就可以直接返回了。

整体流程为：

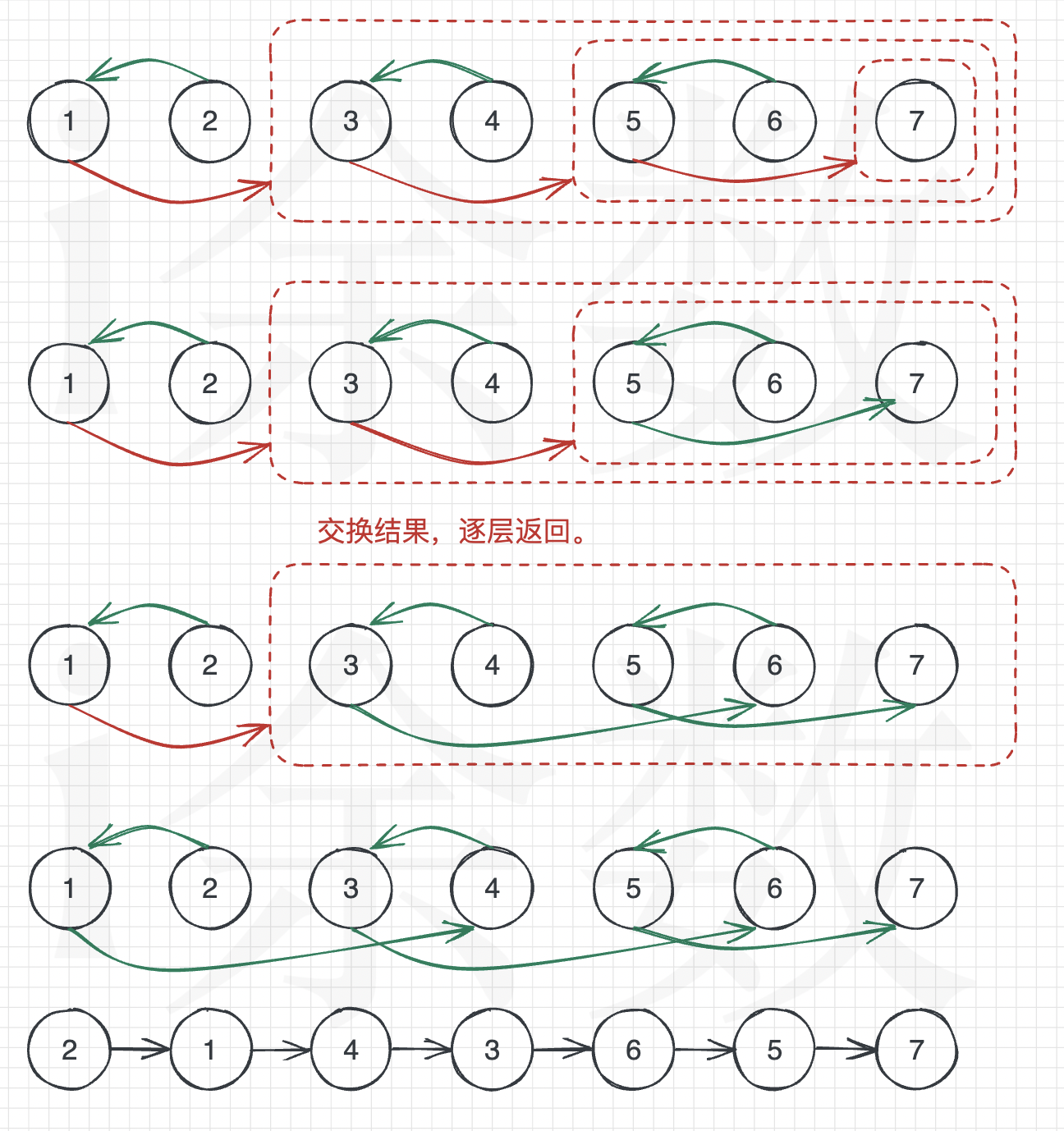
Java 代码实现

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode swapPairs(ListNode head) {

        if(head == null || head.next == null){
            return head;
        }

        ListNode next = head.next;
        ListNode nextHead = next.next;

        // 交换
        next.next = head;
        head.next = swapPairs(nextHead);

        return next;
    }

    
}

Go 代码实现

/**
 * Definition for singly-linked list.
 * type ListNode struct {
 *     Val int
 *     Next *ListNode
 * }
 */
func swapPairs(head *ListNode) *ListNode {

    if head == nil || head.Next == nil {
        return head
    }


    nextNode := head.Next
    nextHead := nextNode.Next

    // 交换
    nextNode.Next = head
    head.Next = swapPairs(nextHead)


    return nextNode
}

复杂度分析

时间复杂度： $O (N)$ ， $N$ 为节点个数，每两个节点计算一次，时间复杂度为 $O (1)$ 。总共需要计算 $(N + 1) /2$ 次，忽略常数后总时间复杂度为 $O (N)$ 。

空间复杂度： $O (N)$ ，空间复杂度主要取决于递归调用栈的深度，为 $(N + 1) /2$ ，忽略常数后总空间复杂度为 $O (N)$ 。

迭代解法

首先为了第一组（即前两个节点）和后面组的交换逻辑保持一致，在最前面加入一个 protect 节点，最后直接返回 protect.next 即为答案。

如下图所示：每一个组的交换策略都是一样的。即第二个节点指向第一个节点，第一个节点指向下一组的头节点。

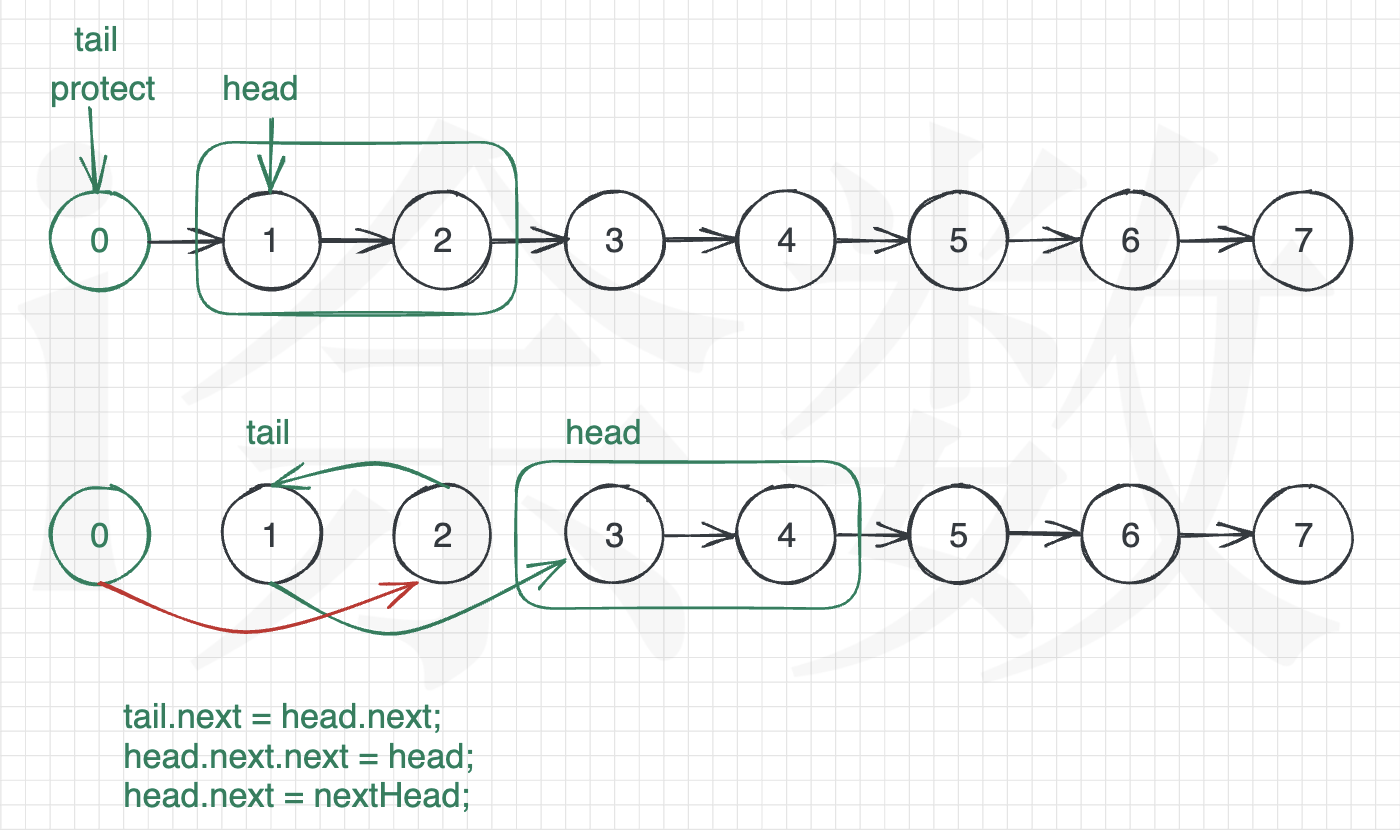
然后需要特别主要的是，因为上一组交换的时候还不知道下一组的结果，所以上一组和下一组的链接可能是错误的，需要在下一组交换完成后，修正一下上下两组的链接，即将上一组的 tail 节点指向当前组交换完后的新的 head 节点。

每次往后移动一组，head 节点变为下一组的头节点，tail 变成上一组结果的尾节点。

Java 代码实现

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode swapPairs(ListNode head) {

        if(head == null){
            return null;
        }

        // 保护节点
        ListNode protect = new ListNode(0, head);

        //已迭代过的尾巴节点
        ListNode tail = protect;

        // 当后面至少还有两个节点的时候，需要继续迭代
        while(tail.next != null && tail.next.next != null){
                
            // 交换
            // 上一组的末尾 --> 本组的第二个节点
            // 本组的第二个节点--> 本组的开头

            head = tail.next;
            ListNode secondNode = head.next;
            ListNode nextHead = secondNode.next;

            
            tail.next = head.next;
            head.next.next = head;
            head.next = nextHead;

            tail = head;
        }

        return protect.next;
    }
}

Go 代码实现

/**
 * Definition for singly-linked list.
 * type ListNode struct {
 *     Val int
 *     Next *ListNode
 * }
 */
func swapPairs(head *ListNode) *ListNode {

    if head == nil || head.Next == nil {
        return head
    }

    protect := &ListNode{0, head}
    tail := protect

    // 当后面至少还有两个节点的时候，需要继续迭代
    for tail.Next != nil && tail.Next.Next != nil {
        // 交换
        // 上一组的末尾 --> 本组的第二个节点
        // 本组的第二个节点--> 本组的开头

        head = tail.Next
        secondNode := head.Next
        nextHead := secondNode.Next

            
        tail.Next = head.Next
        head.Next.Next = head
        head.Next = nextHead

        tail = head;
    }

    return protect.Next


}