数据结构05：树的定义与双亲、孩子表示法[更新中]

news2024/11/6 21:41:17

参考用书：王道考研《2024年 数据结构考研复习指导》

参考用书配套视频：5.1.1 树的定义和基本术语_哔哩哔哩_bilibili

特别感谢： Chat GPT老师[部分名词解释、修改BUG]、BING老师[封面图]~

备注：博文目前是未完成的状态，如题，目前只写了树的存储结构~~本博文篇幅较长，完成时间初步预计为23.06.17~ 🥲

毕竟我的编程水平就是个两脚Bug生成兽，经常1段代码可以卡1天~

考研笔记整理，内容预计包含树、二叉树与森林的基本概念、存储结构，构造与遍历、树、森林与二叉树的转换，代码为C++~考研一起加油~ 🫡

第1版：查资料、写BUG、画导图、画配图ing~

目录

目录

目录

思维导图

树

树的概念

树的基本术语

树的基本性质

树的存储结构

双亲表示法

孩子表示法

结语

备注：此部分待二叉树、森林部分的博文完成后补充~

思维导图

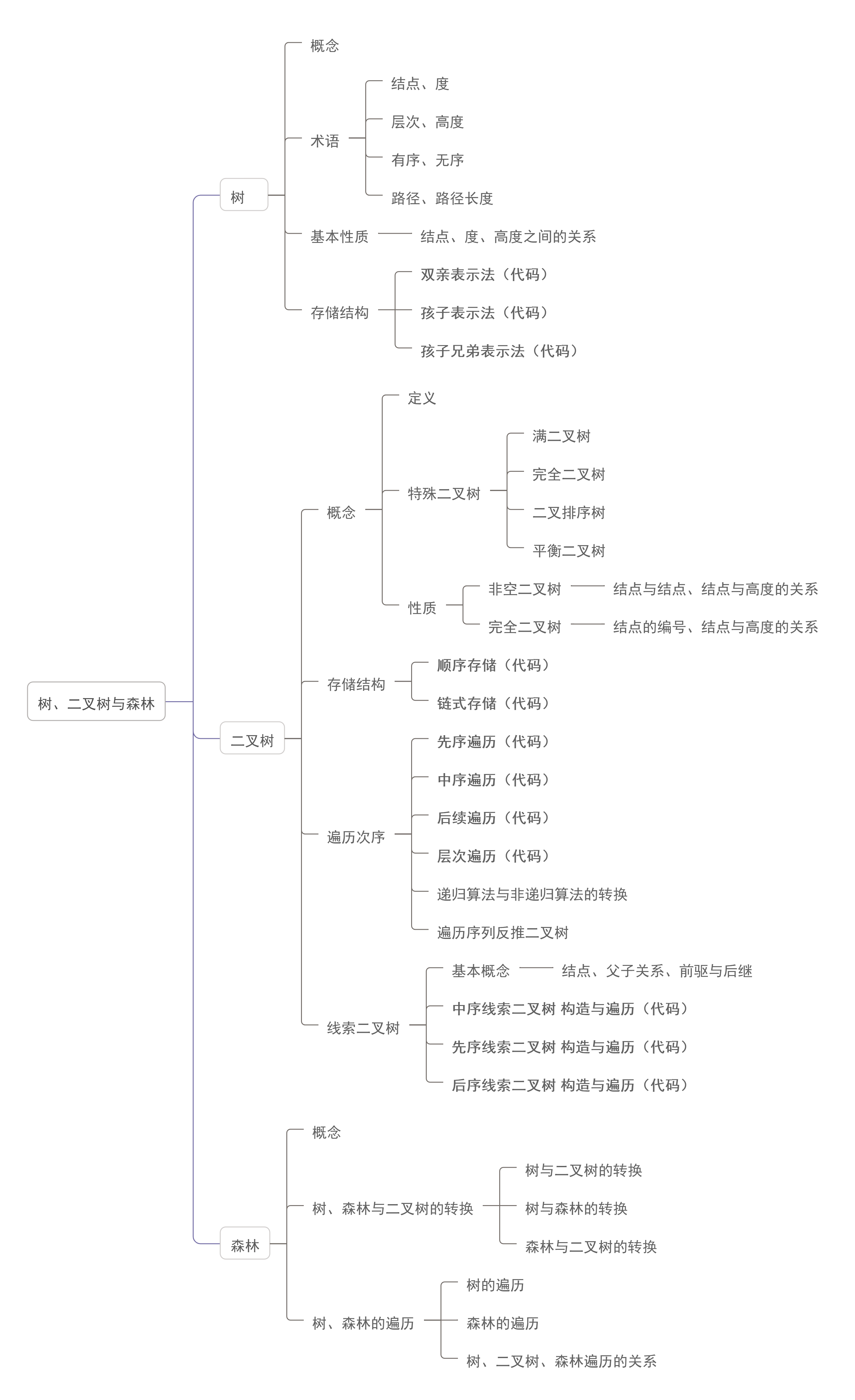
树

树的概念

树的定义：树是n（n≥0）个结点的有限集。当n=0时，称为空树。在任意一棵非空树应满足：

  • 有且仅有一个特定的称为根的结点。
  • 当n＞1时，其余结点可分为m(m>0)个互不相交的有限集T1，T2，...，Tm，其中每个集合本身又是一棵树，并且称为根的子树。 //因此，树是递归的数据结构

树的基本术语

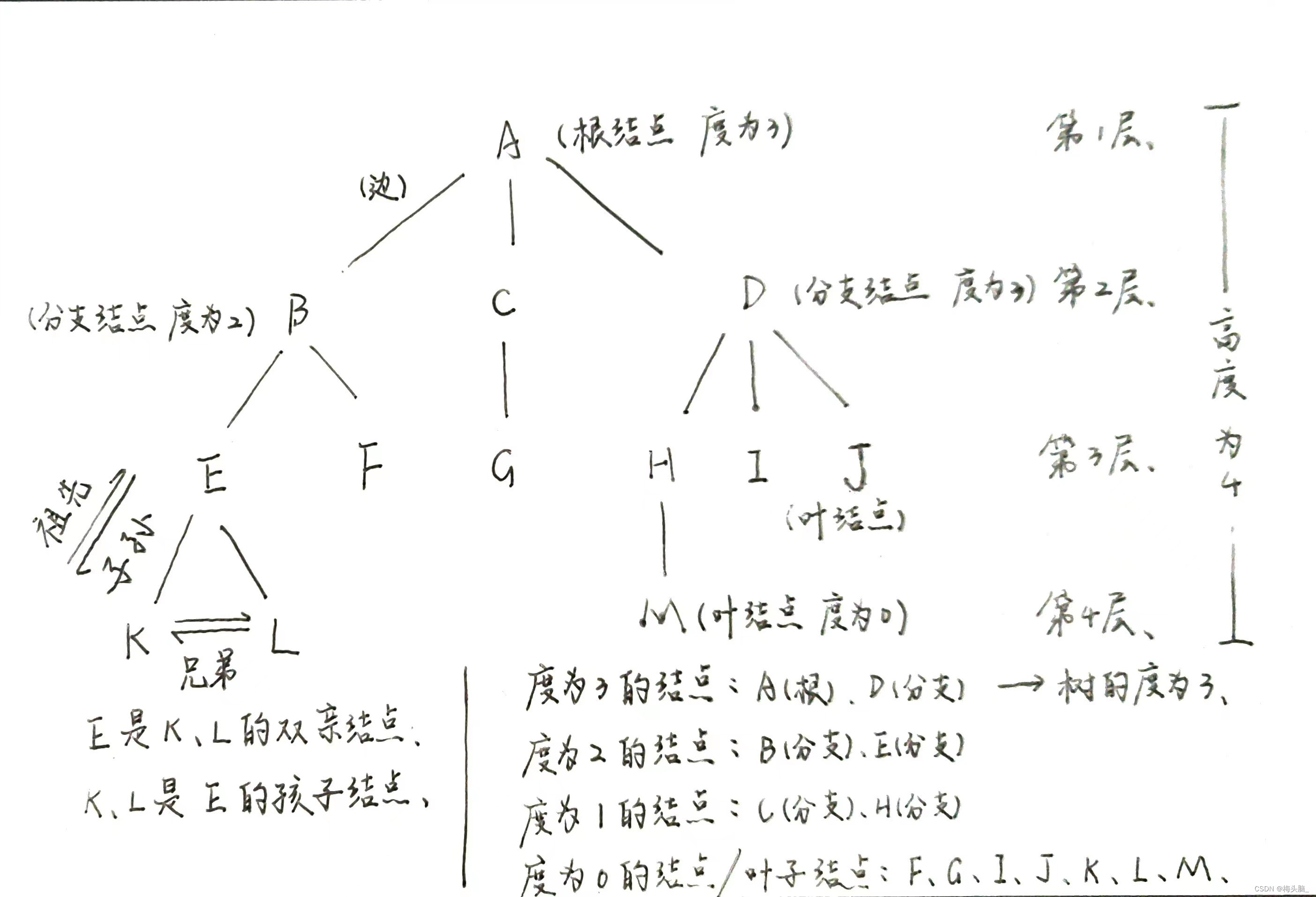
图：树的图形表示+术语注释 

 （1）结点、度

  • 结点：一种数据结构，包含数据和对一个或多个其他节点的引用（例如：指针）。
    • 根结点：树的根节点没有前驱，除根结点以外的所有结点有且仅有1个前驱；
    • 分支结点：除根节点外，度＞0的结点称为分支结点；
    • 分支结点：除根节点外，度 = 0的结点称为分支结点；
  • 结点关系：
    • 祖先结点：从根结点到指定结点的路径上的所有结点，例如结点A、B、E均为结点K的祖先结点；
    • 子孙结点：从指定结点到叶子点的路径上的所有结点，例如结点K、L、F均为结点B的子孙结点；
    • 双亲结点：祖先结点中最接近指定结点的结点，例如结点E是结点K、L的双亲结点。
    • 孩子结点：子孙结点中最接近指定结点的结点，例如结点E、F是结点B的孩子结点。
    • 兄弟结点：具有相同父节点的两个结点，例如结点K与结点L是兄弟结点。
  • 度数：
    • 结点的度：树中一个结点的孩子个数称为度数。
    • 树的度：树中结点的最大度数称为数的度。例如图中结点的度数为3，因此这棵树的结点就是3。

（2）层次、深度、高度：

  • 层次：一个节点的层级是从根节点到该节点的边数。
  • 高度：树中结点的最大层数。

（3）路径：

  • 路径：两个结点之间的路径是由这两个结点之间所经过的结点序列构成的；
  • 结点的路径长度：两个指定结点路径上经过的边的个数。
  • 树的路径长度：树根到每个结点的路径长度的总和。

（4）有序、无序：

  • 有序树：是节点按特定顺序排列的树，结点之间不能互换，例如二叉搜索树。
  • 无序树：是指节点未按任何特定顺序排列的树。

树的基本性质

（1）结点与结点、结点与边

  • n个结点的树 有 n-1条边；// 根节点无前驱，因此无指向根结点的边~
  • 树中的结点数 - 1 =\sum所有结点的度数； // 结点的度数代表孩子结点的个数，根节点为特殊的无前驱的结点，因此需要 -1；

（2）结点与度

  • 度为m的树，在第 i 层上结点数 ≤ m^(i-1)； // 按照结点的度均为m的情况考虑，第1层最多有m^(1-1)=1个结点，第2层最多有m^(2-1)=m个结点...递推可求~

（3）结点与高

  • 高度为h的m叉树 结点数 n ≤ （m^h -1）/（m-1）； // 等比公式可求，Sn=首项（1-公比的n次方）/（1-公比）

嗯，这个我们以满3叉树(m=3)举栗：

结点与高度的公式推算
层数(h)本层最多结点数首层累加至本层结点数
3叉树第1层m^（h-1）=3^（1-1）= 13^0 = 1
3叉树第2层m^（h-1）=3^（2-1）= 33^0 + 3^1 = 4
3叉树第3层m^（h-1）=3^（3-1）= 93^0 + 3^1 + 3^2 = 13
3叉树第4层m^（h-1）=3^（4-1）= 273^0 + 3^1 + 3^2+ 3^3 = 40
.........
3叉树第h层m^（h-1）=3^（h-1）

3^0 + 3^1 + 3^2+ ... +3^（h-1）

=  1 x（1- 3^h）/（1-3）

=（3^h -1）/ （3-1）

m叉树第h层m^（h-1）（m^h -1）/ （m-1）

树的存储结构

双亲表示法

描述：这种存储结构采用一组连续空间来存储每个结点，同时在每个结点中增加一个伪指针，指示其双亲结点在数组中的位置。

特点：

  • 简洁直观：相比其它存储方式易于理解与实现。
  • 存储结构：顺序存储和链式存储均可实现，其中顺序存储较为常见。
  • 存取效率：可以很快得到每个结点的双亲结点，但求孩子结点时需要遍历整个结构；不过这并不是硬伤，可以根据需要在结构体中增加一个用于存放孩子结点的伪指针。// 所以这里叫做顺序存储法是不是比双亲存储法更合适一些~~
  • 是否有序：双亲表示法不适合表示有序树，更适合表示无序树，因为无序树中节点的子节点没有明确的顺序关系。

图示：源于《王道》教材图5.14 树的双亲表示法

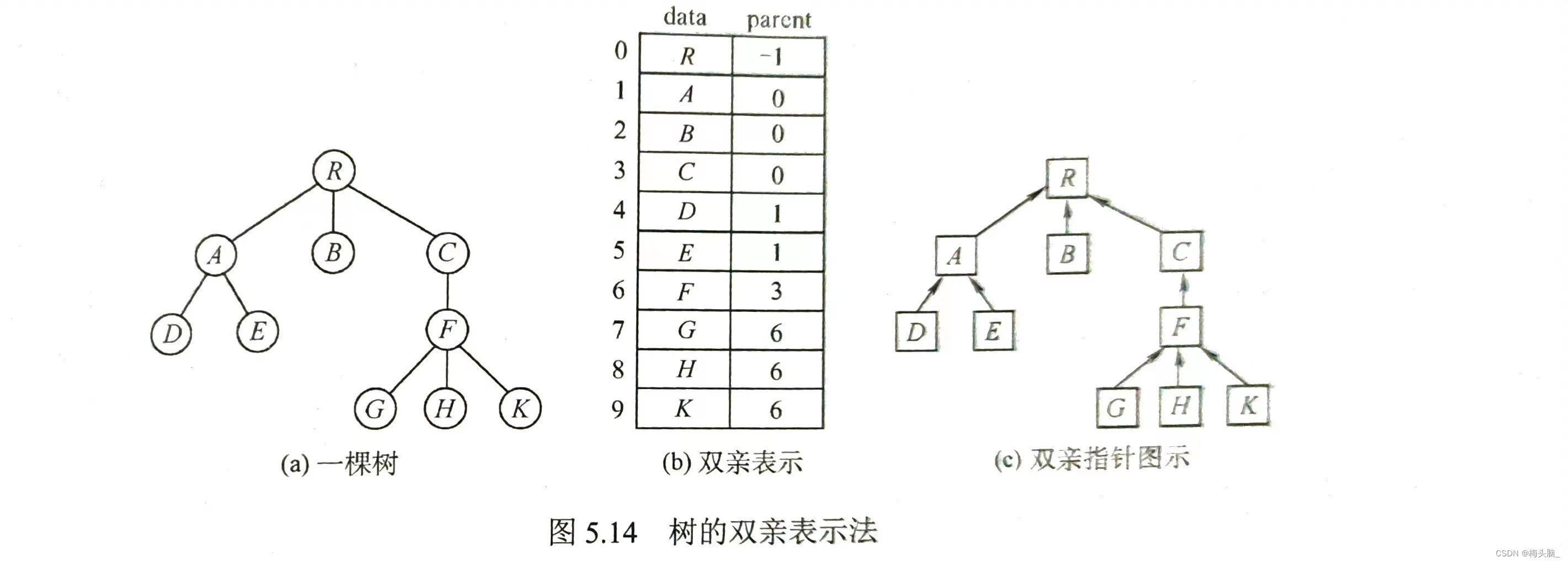
双亲表示法 核心代码：

#define MAX_TREE_SIZE 100   //树中可以存储的结点数

typedef struct{     //树中结点的结构，该结构有两个字段
    ElemType data;   //该字段存储结点的数据元素
    int parent;      //该字段存储结点的双亲指针（伪指针）
}PTNode;

typedef struct{     //树的结构，该结构有两个字段
    PTNode nodes[MAX_TREE_SIZE];   //结构数组，用于存储树中的结点
    int n;                         //树中的结点数
}PTree;

双亲表示法 案例：

要求：1 存储上面图示中的树，并顺序输出结点；2 按值查找某节点，并寻找其父结点与子节点；3 按位查找某节点，并输出其祖先结点与子孙结点~

思路：

LocateElem封装按值查找函数，并寻找双亲与孩子结点~

  1. 用参数i记录并遍历本结点的位序；

  2. 找到目标结点后，输出当前结点的信息，将父结点的信息赋值给j并输出；

  3. 通过循环寻找并输出孩子结点的信息，同时记录子结点的数量；如果子结点的数量为0，则输出没有子结点的提示信息；[这一步时间开销会很高，仅寻找相邻结点]；

  4. 如果遍历到末尾没有找到结点，则输出没有该结点的提示信息。

get封装按位查找函数，并寻找祖先与子孙结点~

  1. 判断树中是为空，如果是，返回错误；如果否，继续执行；
  2. 判断值是否越界，如果是，返回错误；如果否，继续执行；
  3. 输出目标结点的data与parent；

  4. 通过递归寻找并输出祖先/子孙结点的信息，同时记录子结点的数量；如果子结点的数量为0，则输出没有子结点的提示信息；如果父节点已为根结点，则反馈到第2步；[这一步时间开销会很高，可寻找所有祖先/子孙结点]； 

#include <iostream>
#define MAX_TREE_SIZE 100  // 树的最大节点数量

typedef struct {
    char data;  // 节点数据
    int parent;  // 双亲节点的索引
} PTNode;

typedef struct {
    PTNode nodes[MAX_TREE_SIZE];  // 节点数组
    int n;  // 当前节点数目
} PTree;

// 初始化树对象
void InitTree(PTree* tree) {
    for (int i = 0; i < MAX_TREE_SIZE; i++) {
        tree->nodes[i].data = 0;  // 将节点数据初始化为0
        tree->nodes[i].parent = -1;  // 将节点的双亲索引初始化为-1
    }
    tree->n = 0;  // 初始化节点数量为0
}

// 添加节点到树中
void addNode(PTree* tree, char data, int parentIndex) {
    if (tree->n >= MAX_TREE_SIZE) {  // 如果树已满，不能再添加数据
        std::cout << "错误：树已满，不能再添加数据。\n";
        return;
    }

    PTNode newNode;
    newNode.data = data;  // 设置新节点的数据

    if (parentIndex < 0) {
        newNode.parent = -1;  // 如果双亲索引小于0，则表示没有双亲节点
    }
    else {
        newNode.parent = parentIndex;  // 否则，将双亲索引设置为给定的索引值
    }

    tree->nodes[tree->n] = newNode;  // 将新节点添加到节点数组中
    tree->n++;  // 更新节点数量
}

// 按值查找节点
void LocateElem(const PTree* tree, char data) {
    int i, j;
    int childCount = 0;
    int firstChildPos = -1;

    for (i = 0, j = -1; i < tree->n; i++) {
        if (tree->nodes[i].data == data) {  // 如果找到匹配的节点
            std::cout << "找到结点 " << data << std::endl;
            std::cout << "当前结点信息：" << "位置: " << i << ", 数据: " << tree->nodes[i].data << ", 双亲位置: " << tree->nodes[i].parent << std::endl;

            j = tree->nodes[i].parent;
            if (j != -1) {
                std::cout << "父节点信息：" << "位置: " << j << ", 数据: " << tree->nodes[j].data << ", 双亲位置: " << tree->nodes[j].parent << std::endl;
            }

            for (int k = 0; k < tree->n; k++) {
                if (tree->nodes[k].parent == i) {
                    if (childCount == 0) {
                        firstChildPos = k;
                    }
                    std::cout << "子节点信息：" << "位置: " << k << ", 数据: " << tree->nodes[k].data << ", 双亲位置: " << tree->nodes[k].parent << std::endl;
                    childCount++;
                }
            }

            if (childCount == 0) {
                std::cout << "该结点没有子节点" << std::endl;
            }
            else {
                std::cout << "子节点数量: " << childCount << std::endl;
                //std::cout << "第一个子节点信息：" << "位置: " << firstChildPos << ", 数据: " << tree->nodes[firstChildPos].data << ", 双亲位置: " << tree->nodes[firstChildPos].parent << std::endl;
            }

            return;
        }
    }

    std::cout << "未找到结点 " << data << std::endl;
}

// 获取节点的子孙节点
void GetOffspring(const PTree& tree, int index) {
    if (index < 0 || index >= tree.n) {  // 检查索引是否越界
        std::cout << "错误：索引越界。\n";
        return;
    }

    const PTNode& currentNode = tree.nodes[index];

    std::cout << "结点位置: " << index << ", 数据: " << currentNode.data << ", 父节点位置: " << currentNode.parent << std::endl;

    int childCount = 0;

    for (int i = 0; i < tree.n; i++) {
        if (tree.nodes[i].parent == index) {  // 如果节点的双亲索引与给定索引相等，则表示是其子节点
            childCount++;
            GetOffspring(tree, i);  // 递归调用以获取孩子节点的子节点
        }
    }

    if (childCount == 0) {
        std::cout << "该结点没有孩子结点。\n";
    }
}

// 获取节点的祖先节点
void GetAncestors(const PTree& tree, int index) {
    if (index < 0 || index >= tree.n) {  // 检查索引是否越界
        std::cout << "错误：索引越界。\n";
        return;
    }

    const PTNode& currentNode = tree.nodes[index];

    std::cout << "结点位置: " << index << ", 数据: " << currentNode.data << ", 父节点位置: " << currentNode.parent << std::endl;

    int parentIndex = currentNode.parent;
    if (parentIndex >= 0) {
        GetAncestors(tree, parentIndex);  // 递归调用以获取祖先节点的祖先节点
    }
}

int main() {
    PTree newtree;
    // 初始化树对象
    InitTree(&newtree);

    // 增加节点
    char data;
    int parentIndex;
    while (std::cout << "输入结点: " && std::cin >> data && data != '\\') {
        std::cout << "输入结点的双亲位置: ";
        std::cin >> parentIndex;
        addNode(&newtree, data, parentIndex);
    }

    std::cout << std::endl;

    // 输出结点
    for (int i = 0; i < newtree.n; i++) {
        std::cout << "结点位置: " << i << ", 数据: " << newtree.nodes[i].data << ", 父节点位置: " << newtree.nodes[i].parent << std::endl;
    }

    std::cout << std::endl;

    // 输出按值查找结点信息
    char target1;
    std::cout << "请输入要按值查找的结点: ";
    std::cin >> target1;
    LocateElem(&newtree, target1);

    std::cout << std::endl;

    // 输出子孙结点
    int targetIndex1;
    std::cout << "寻找该位序的子孙结点: ";
    std::cin >> targetIndex1;
    GetOffspring(newtree, targetIndex1);

    std::cout << std::endl;

    // 输出祖先结点
    int targetIndex2;
    std::cout << "寻找该位序的祖先结点: ";
    std::cin >> targetIndex2;
    GetAncestors(newtree, targetIndex2);

    return 0;
}

运行的效果如下图所示：

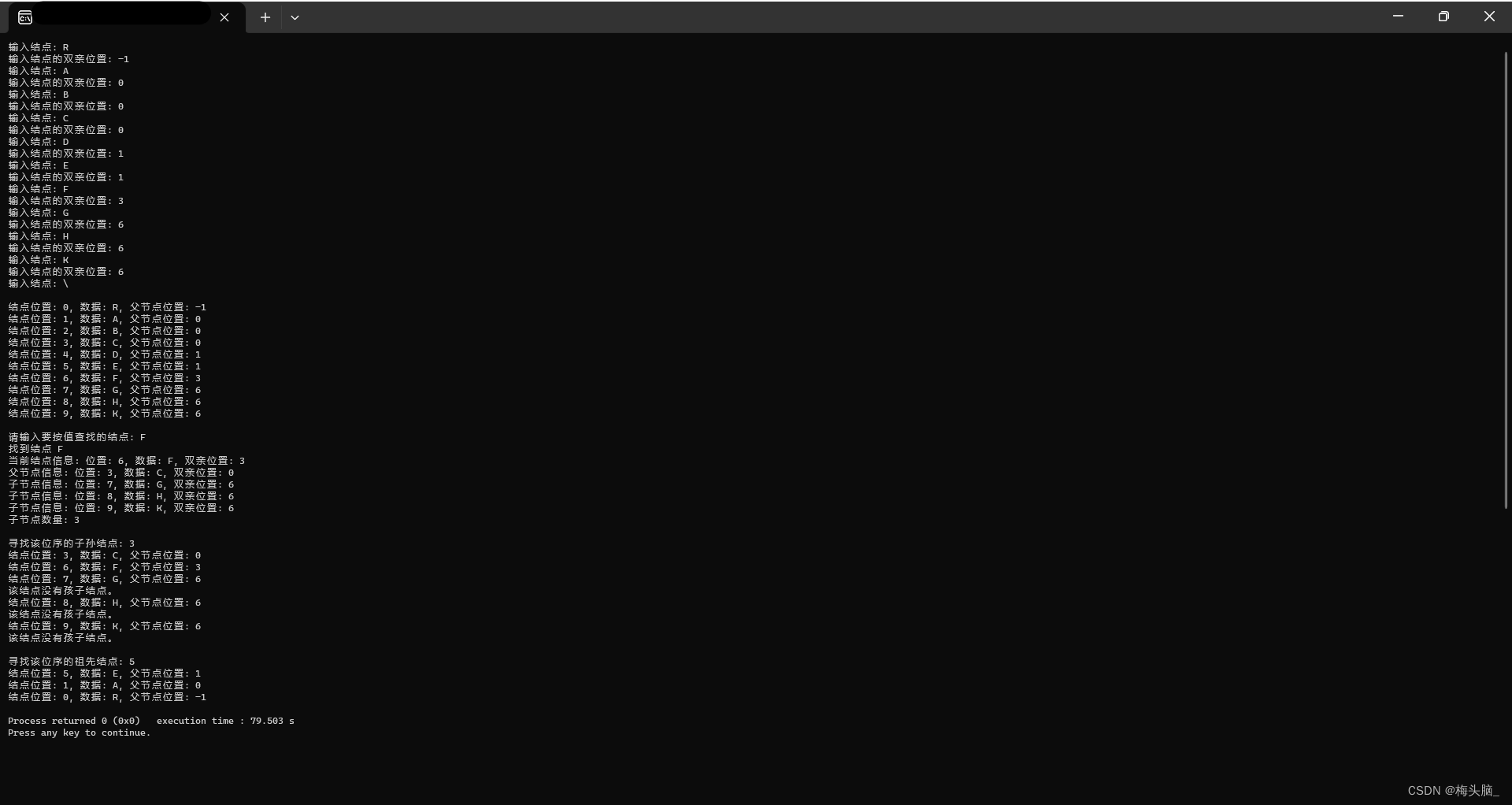
孩子表示法

描述：将每个结点都用单链表链接起来的线性结构，此时n个结点就有n个孩子链表（叶节点的孩子链表为空链表）。

特点：

  • 存储结构：顺序存储法通常由顺序表和链表共同构成。在这种存储方式中，树的整体结构使用顺序表来表示，而每个结点则使用链表来表示其孩子结点。
  • 存取效率：可以很快得到每个结点的孩子结点，方便地动态添加孩子节点，但求双亲结点时需要遍历指针域所指向的n个孩子链表。
  • 是否有序：适用于任意树的存储，包括有序树。由于每个节点的孩子节点都以单链表的形式链接，因此可以灵活地表示任意数量的子节点，并且可以按照节点在链表中的顺序确定子节点的顺序。

图示：源于《王道》教材图5.15 树的孩子表示法

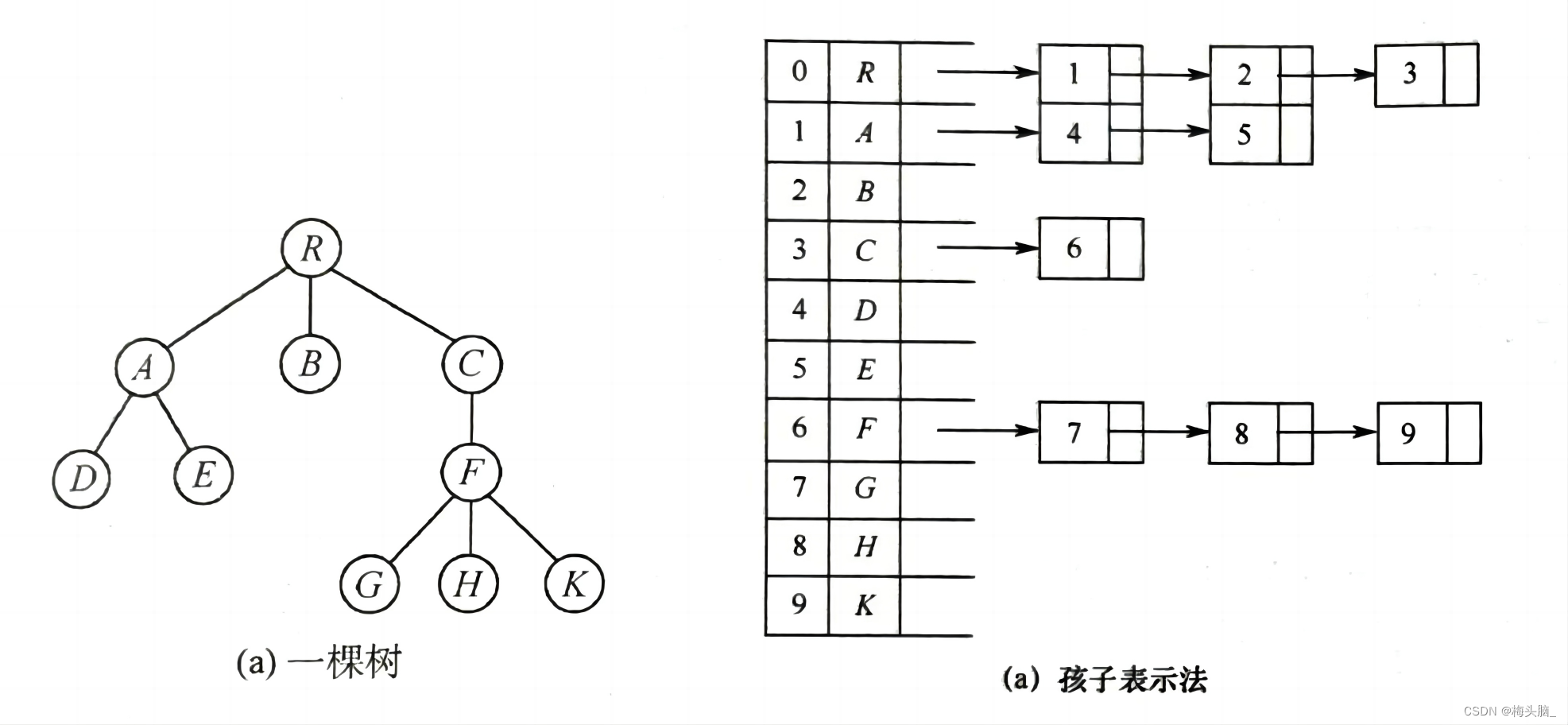
孩子表示法 案例：

要求：存储上面图示中的树，并顺序输出结点~

备注：

  1. 构建树的核心思想是队列~👉：数据结构03：栈、队列和数组_梅头脑-CSDN博客
  2. 采用其它方法构造树很麻烦且很容易出Bug的，真的~经过了多次的失败打击，考虑到时间有限，最后还是找gpt老师帮我重构逻辑重写了一份代码~😢😢
  3. 好像不是很重要的知识点~

思路：

  1. 定义了两个结构体：CTNode和CTree。CTNode结构体表示树的节点，包含了节点的数据元素和一个指向子节点的指针数组；CTree结构体表示整个树，包含了根节点的指针。

  2. 初始化树对象：initTree()函数用于创建一个空的树对象，并返回指向该对象的指针。

  3. 创建节点：createNode()函数用于创建一个新的节点，并返回指向该节点的指针。该函数接受节点的数据元素作为参数。

  4. 添加子节点：addChild()函数用于将一个节点添加为另一个节点的子节点。该函数接受父节点和子节点的指针作为参数，并将子节点添加到父节点的子节点指针数组中。

  5. 构建树：buildTree()函数用于根据用户的输入构建树。函数首先读取根节点的数据元素，然后使用循环来依次读取每个节点的子节点数量和数据元素，并将子节点添加到相应的父节点中。这个过程使用了一个结点队列来辅助构建树，确保树的每个节点都被正确处理。

  6. 输出树的结构：printTree()函数用于输出树的结构。函数使用了层次遍历的方式，从根节点开始，逐层输出节点的数据元素和子节点的数据元素。

#include <iostream>
#include <vector>

struct CTNode {
    char data;                 // 结点数据
    std::vector<CTNode*> children;  // 子节点指针
};

struct CTree {
    CTNode* root;  // 根节点指针
};

// 创建新的结点
CTNode* createNode(char data) {
    CTNode* newNode = new CTNode();
    newNode->data = data;
    return newNode;
}

// 添加子节点
void addChild(CTNode* parent, CTNode* child) {
    parent->children.push_back(child);
}

// 初始化树
CTree* initTree() {
    CTree* tree = new CTree();
    tree->root = nullptr;
    return tree;
}

// 构建树
void buildTree(CTree* tree) {
    char data;
    std::cout << "输入根节点数据: ";
    std::cin >> data;

    // 创建根节点
    CTNode* root = createNode(data);
    tree->root = root;

    std::vector<CTNode*> nodeQueue;  // 结点队列，用于辅助构建树
    nodeQueue.push_back(root);

    while (!nodeQueue.empty()) {
        CTNode* currentNode = nodeQueue.front();
        nodeQueue.erase(nodeQueue.begin());

        int childCount;
        std::cout << "输入节点 " << currentNode->data << " 的子节点数量: ";
        std::cin >> childCount;

        for (int i = 0; i < childCount; i++) {
            char childData;
            std::cout << "输入子节点 " << i + 1 << " 的数据: ";
            std::cin >> childData;

            // 创建子节点
            CTNode* childNode = createNode(childData);

            // 添加子节点到当前节点
            addChild(currentNode, childNode);

            // 将子节点加入队列，继续构建子树
            nodeQueue.push_back(childNode);
        }
    }
}

// 输出树的结构
void printTree(const CTree* tree) {
    if (tree->root == nullptr) {
        std::cout << "树为空。\n";
        return;
    }

    std::cout << "树的结构:\n";

    std::vector<const CTNode*> nodeQueue;  // 结点队列，用于层次遍历
    nodeQueue.push_back(tree->root);

    while (!nodeQueue.empty()) {
        const CTNode* currentNode = nodeQueue.front();
        nodeQueue.erase(nodeQueue.begin());

        std::cout << "结点数据: " << currentNode->data;

        if (!currentNode->children.empty()) {
            std::cout << "，子节点数据: ";
            for (const CTNode* child : currentNode->children) {
                std::cout << child->data << " ";
                nodeQueue.push_back(child);
            }
        }

        std::cout << "\n";
    }
}

int main() {
    CTree* tree = initTree();  // 初始化树

    buildTree(tree);  // 构建树

    std::cout << "\n";
    printTree(tree);  // 输出树的结构

    delete tree;  // 释放内存

    return 0;
}

 运行的效果如下图所示：

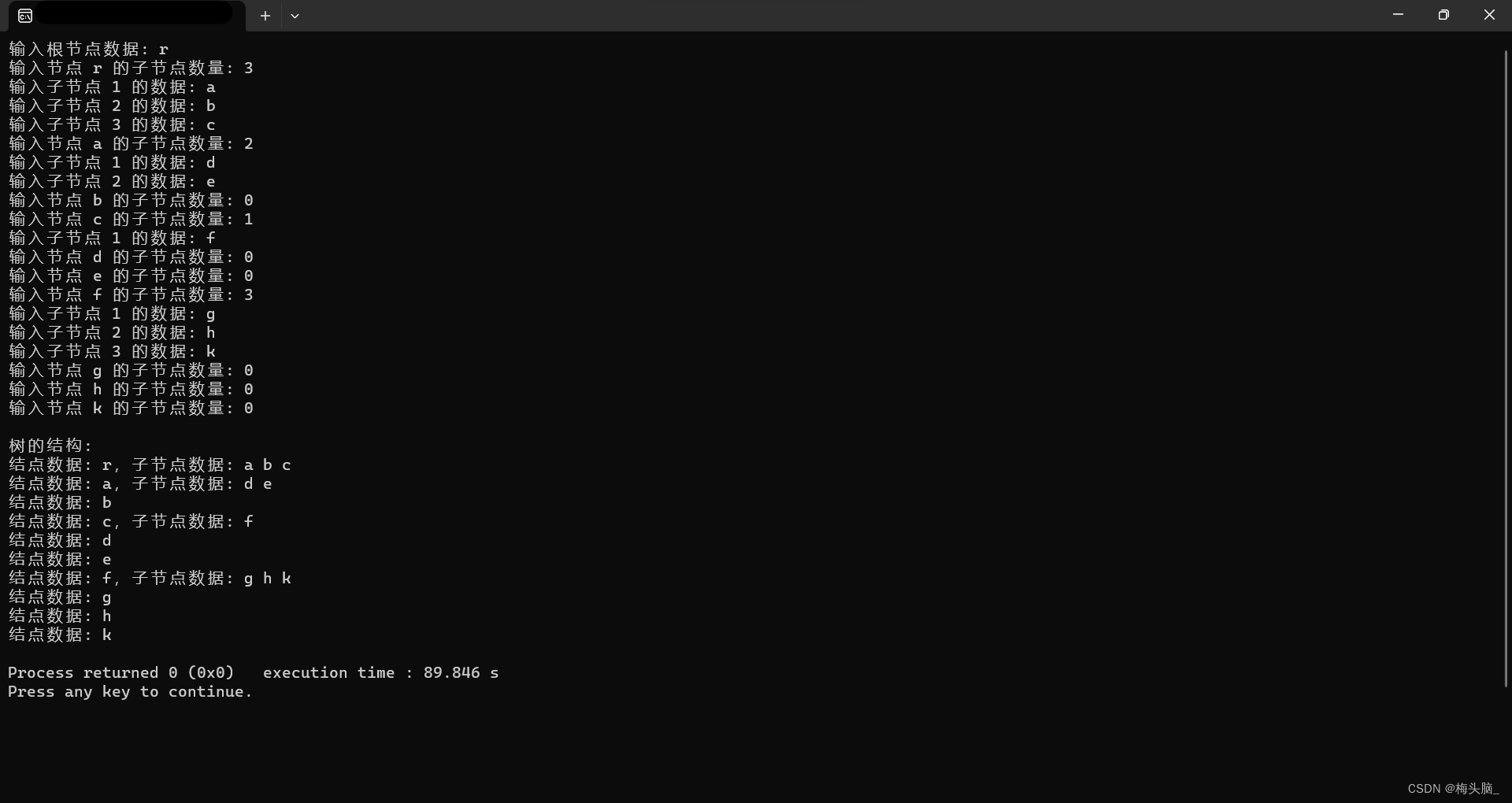
结语

博文未完待续，写得模糊或者有误之处，欢迎小伙伴留言讨论与批评~😶‍🌫️

码字不易，若有所帮助，可以点赞支持一下博主嘛？感谢~🫡

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/625032.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Web安全：拿到 Web 服务器 最高权限.（vulntarget 靶场 A）

Web安全：拿到 Web 服务器 最高权限.（vulntarget 靶场 A）

Web安全&#xff1a;拿到 Web 服务器 最高权限. Web 服务器一般指网站服务器&#xff0c;是指驻留于因特网上某种类型计算机的程序&#xff0c;可以处理浏览器等Web客户端的请求并返回相应响应&#xff0c;也可以放置网站文件&#xff0c;让全世界浏览&#xff1b;可以放置数据…
阅读更多...
43 最佳实践-性能最佳实践-IOThread配置

43 最佳实践-性能最佳实践-IOThread配置

文章目录 43 最佳实践-性能最佳实践-IOThread配置43.1 概述43.2 配置说明 43 最佳实践-性能最佳实践-IOThread配置 43.1 概述 KVM平台上&#xff0c;对虚拟磁盘的读写在后端默认由QEMU主线程负责处理。这样会造成如下问题&#xff1a; 虚拟机的I/O请求都由一个QEMU主线程进行…
阅读更多...
基于springboot的数码论坛系统设计（Java、MySQL、B/S）

基于springboot的数码论坛系统设计（Java、MySQL、B/S）

wx供重浩&#xff1a;创享日记 对话框发送&#xff1a;数码论坛 获取源码源文件论文报告PPT 网络的广泛应用给生活带来了十分的便利。所以把数码论坛与现在网络相结合&#xff0c;利用java技术建设数码论坛系统&#xff0c;实现数码论坛的信息化。则对于进一步提高数码论坛发展…
阅读更多...
Linux 下pause函数是如何实现的？

Linux 下pause函数是如何实现的？

当你在程序中调用 pause() 函数时&#xff0c;它会使得你的程序停止执行&#xff0c;直到有一个信号被捕获。这是通过系统调用实现的。系统调用会使得程序从用户模式切换到内核模式。 这里是 pause() 函数的基本工作原理&#xff1a; 当你的程序调用 pause() 函数时&#xff…
阅读更多...
python基础知识(十):类

python基础知识(十):类

目录 1. 类和方法的概念2. 类的定义3. 类的继承4. 重写父类的方法 1. 类和方法的概念 类&#xff1a;用来描述具有相同的属性和方法的对象的集合。它定义了该集合中每个对象所共有的属性和方法。对象是类的实例。举个例子&#xff0c;狗类就是狗的集合&#xff0c;每条狗都是狗…
阅读更多...
kali学习笔记（二）

kali学习笔记（二）

一、关闭自动锁屏 关闭自动锁屏对于测试人员来说&#xff0c;可以按照自己的习惯来设置&#xff0c;不然kali会过十分钟就锁屏&#xff0c;有的时候会比较不方便。 1、使用root账号登录&#xff0c;在display设置选项中做如下设置。 2、把休眠选项关掉。 二、创建快照 关机创…
阅读更多...
透视Linux内核，BPF 深度分析与案例讲解

透视Linux内核，BPF 深度分析与案例讲解

本次主要对BPF的部分原理、应用案例上进行一次分析记录。 BPF介绍 当内核触发事件时&#xff0c;BPF虚拟机能够运行相应的BPF程序指令&#xff0c;但是并不是意味着BPF程序能访问内核触发的所有事件。将BPF目标文件加载到BPF虚拟机时&#xff0c;需要确定特定的程序类型&…
阅读更多...
SpringBoot中的定时任务@Scheduled的使用

SpringBoot中的定时任务@Scheduled的使用

1.Scheduled注解介绍 在spring boot的项目中需要使用到定时任务的时候&#xff0c;可以使用Scheduled注解&#xff0c;这只是在一个JVM进程中很适用&#xff0c;如果涉及到服务器是集群的情况下&#xff0c;建议使用任务调度平台。这样任务调度平台会在多台服务器中选择一台进…
阅读更多...
【linux】在Ubuntu下部署nginx——nginx的安装与卸载

【linux】在Ubuntu下部署nginx——nginx的安装与卸载

介绍 这里是小编成长之路的历程&#xff0c;也是小编的学习之路。希望和各位大佬们一起成长&#xff01; 以下为小编最喜欢的两句话&#xff1a; 要有最朴素的生活和最遥远的梦想&#xff0c;即使明天天寒地冻&#xff0c;山高水远&#xff0c;路远马亡。 一个人为什么要努力&a…
阅读更多...
Think PHP6+Swagger3

Think PHP6+Swagger3

swagger是一个解决接口规范化、标准化、文档化的一个组件&#xff0c;既可以直接自动生成resutful接口文档又能进行功能测试的一个web服务。本文是think PHP6结合swagger3的一个记录过程。 composer安装ThinkPHP 一般安装最新稳定版本&#xff0c;不一定是最新版本 composer…
阅读更多...
怎么通过Fiddler对APP进行抓包？以及高级应用场景分析

怎么通过Fiddler对APP进行抓包？以及高级应用场景分析

目录 前言 简单说下Fiddler的抓包原理&#xff1a; 使用fiddler代理远程捕获APP请求 Fiddler高级应用场景介绍 1、url地址重写 fiddler抓包详细教程&#xff1a;全网抓包天花板教程&#xff0c;B站讲的最详细的Fiddler/Charles抓包教学视频。2小时包你学会_哔哩哔哩_bilibi…
阅读更多...
软件测试之路已不再是坦途

软件测试之路已不再是坦途

去年下半年才跳了槽&#xff0c;过程非常顺利&#xff0c;没有经历大家所说的工作荒的境地&#xff0c;所以一直没有直观地感受到软件测试就业形势到底有多严峻。 近来看到一些机构频频发出某某测试员在糟糕的就业形势下逆袭拿下XXW的某厂offer&#xff0c;然后推荐测试进阶课…
阅读更多...
Django学习笔记-配置Docker、Git环境与项目创建

Django学习笔记-配置Docker、Git环境与项目创建

笔记内容转载自AcWing的Django框架课讲义&#xff0c;课程链接&#xff1a;AcWing Django框架课。 CONTENTS 1. 配置Docker环境2. Django项目创建3. Django App创建 1. 配置Docker环境 首先拉取一个 Ubuntu 镜像&#xff1a; docker pull ubuntu:20.04创建容器后进入容器配置…
阅读更多...
Splunk：构建安全监控解决方案（第 1 部分）

Splunk：构建安全监控解决方案（第 1 部分）

在我的网络安全训练营的最后几周&#xff0c;我们的最终项目之一是使用 Splunk Enterprise 为一个名为 VSI&#xff08;虚拟空间工业&#xff09;的虚构组织构建安全监控环境&#xff0c;对于那些可能不知道的人来说&#xff0c;它是一个 SIEM&#xff08;安全信息和事件管理器…
阅读更多...
科一容易忘、容易混的点——图类

科一容易忘、容易混的点——图类

注意行人 和 人行横道区别 注意行人&#xff1a;黄色&#xff0c;里面是什么就注意什么 人行横道&#xff1a;正方形 “不得” xxx 的 就选择 【正确】 点火开关 1、LOCK档&#xff1a;这是一个锁止档&#xff0c;功能是当除了防盗系统和车内小灯以外&#xff0c;电路是完全关…
阅读更多...
【Redis应用】用户签到统计连续签到(三)

【Redis应用】用户签到统计连续签到(三)

&#x1f697;Redis应用学习第三站~ &#x1f6a9;本文已收录至专栏&#xff1a;Redis技术学习 签到功能是我们非常常见的一个功能&#xff0c;几乎在每个app中都能碰到&#xff0c;让我们一起看看如何实现吧~ 一.BitMap用法引入 我们针对签到功能完全可以通过mysql来完成&am…
阅读更多...
Python基于指定范围筛选并剔除Excel表格中的数据

Python基于指定范围筛选并剔除Excel表格中的数据

本文介绍基于Python语言&#xff0c;读取Excel表格文件&#xff0c;基于我们给定的规则&#xff0c;对其中的数据加以筛选&#xff0c;将不在指定数据范围内的数据剔除&#xff0c;保留符合我们需要的数据的方法。 首先&#xff0c;我们来明确一下本文的具体需求。现有一个Exce…
阅读更多...
【JavaScript】讲解JavaScript的基础知识并且配有案例讲解

【JavaScript】讲解JavaScript的基础知识并且配有案例讲解

&#x1f38a;专栏【 前端易错合集】 &#x1f354;喜欢的诗句&#xff1a;更喜岷山千里雪 三军过后尽开颜。 &#x1f386;音乐分享【如愿】 大一同学小吉&#xff0c;欢迎并且感谢大家指出我的问题&#x1f970; 目录 &#x1f381;JavaScript嵌入网页的方式 &#x1f354;a…
阅读更多...
LVS--DR集群部署

LVS--DR集群部署

LVS--DR集群 一、DR模式原理二、实验 一、DR模式原理 原理&#xff1a;首先负载均衡器接收到客户的请求数据包时&#xff0c;根据调度算法决定将请求发送给哪个后端的真实服务器&#xff08;RS&#xff09;。然后负载均衡器就把客户端发送的请求数据包的目标MAC地址改成后端真…
阅读更多...
PCI Express架构概述

PCI Express架构概述

目录 1. PCIe 总线概述 2. PCIe 拓扑结构 3. PCIe 分层结构 4. PCIe 事务层类型 5. PCIe 配置和地址空间 1. PCIe 总线概述 PCIe&#xff08;Peripheral Component Interconnect Express&#xff09;是一种用于连接计算机内部硬件设备的高速串行总线。它是在PCI&#xff08…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023