蚁群算法(ant colony algorithm,ACA)是由意大利学者M.Dorigo等人于20世纪90年代初提出的一种新的模拟进化算法,其真实地模拟了自然界蚂蚁群体的觅食行为。M.Dorigo等人将其用于解决旅行商问题(traveling salesman problem,TSP),并取得了较好的实验结果。
近年来,许多专家学者致力于蚁群算法的研究,并将其应用于交通、通信、化工、电力等领域,成功解决了许多组合优化问题,如调度问题(job-shop scheduling problem)、指派问题(quadratic assignment problem)、旅行商问题(traveling salesman problem)等。本章将详细阐述蚁群算法的基本思想及原理,并以实例的形式介绍其应用于解决中国旅行商问题(chineseTSP,CTSP)的情况。
1 理论基础
1.1 蚁群算法基本思想
生物学家研究发现,自然界中的蚂蚁觅食是一个群体性行为,并非单只蚂蚁自行寻找食物。蚂蚁在寻找食物源时,会在其经过的路径上释放一种信息素,并能够感知其他蚂蚁释放的信息素。信息素浓度的大小表征路径的远近,信息素浓度越高,表示对应的路径距离越短。通常,蚂蚁会以较大的概率优先选择信息素浓度较高的路径,并释放一定量的信息素,以增强该条路径上的信息素浓度,这样会形成一个正反馈。最终,蚂蚁能够找到一条从巢穴到食物源的最佳路径,即最短距离。值得一提的是,生物学家同时发现,路径上的信息素浓度会随着时间的推进而逐渐衰减。
将蚁群算法应用于解决优化问题的基本思路为:用蚂蚁的行走路径表示待优化问题的可行解,整个蚂蚁群体的所有路径构成待优化问题的解空间。路径较短的蚂蚁释放的信息素量较多,随着时间的推进,较短的路径上累积的信息素浓度逐渐增高,选择该路径的蚂蚁个数也愈来愈多。最终,整个蚂蚁会在正反馈的作用下集中到最佳的路径上,此时对应的便是待优化问题的最优解。
1.2 蚁群算法解决TSP问题基本原理
本节将用数学语言对上述蚁群算法的基本思想进行抽象描述,并详细阐述蚁群算法用于解决TSP问题的基本原理。
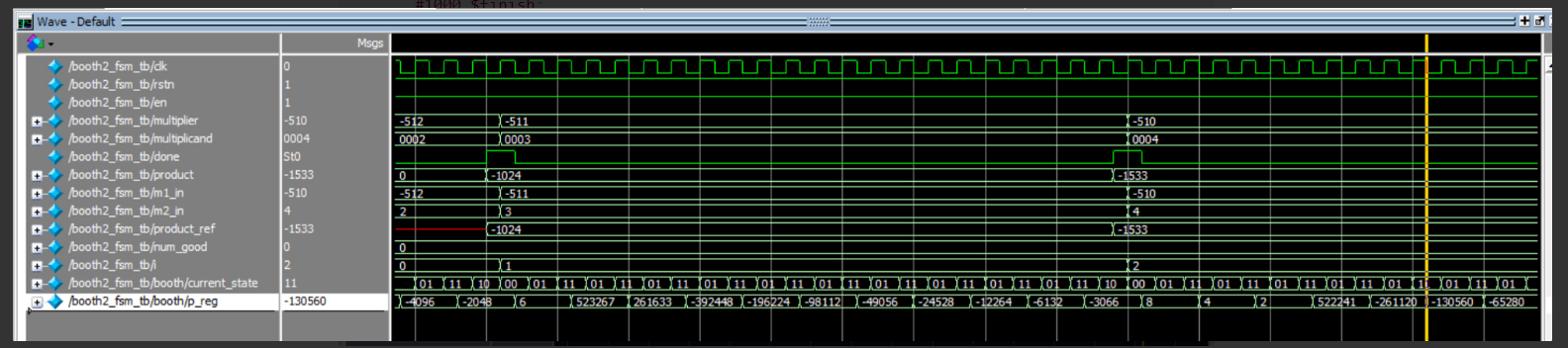
不失一般性,设整个蚂蚁群体中蚂蚁的数量为m,城市的数量为n,城市i与城市j之间的距离为dij(i,j=1,2,…,n),t时刻城市i与城市j连接路径上的信息素浓度为 。初始时刻,各个城市间连接路径上的信息素浓度相同,不妨设为
。初始时刻,各个城市间连接路径上的信息素浓度相同,不妨设为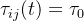 。
。
蚂蚁k(k=1,2,…,m)根据各个城市间连接路径上的信息素浓度决定其下一个访问城市,设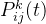 表示t时刻蚂蚁k从城市i转移到城市j的概率,其计算公式为
表示t时刻蚂蚁k从城市i转移到城市j的概率,其计算公式为
其中, 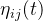 为启发函数,
为启发函数,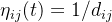 表示蚂蚁从城市i转移到城市j的期望程度;allowk(k=1,2,…,m)为蚂蚁k待访问城市的集合,开始时,allowk中有(n-1)个元素,即包括除了蚂蚁k出发城市的其他所有城市,随着时间的推进,allow;中的元素不断减少,直至为空,即表示所有的城市均访问完毕;α为信息素重要程度因子,其值越大,表示信息素的浓度在转移中起的作用越大;β为启发函数重要程度因子,其值越大,表示启发函数在转移中的作用越大,即蚂蚁会以较大的概率转移到距离短的城市。
表示蚂蚁从城市i转移到城市j的期望程度;allowk(k=1,2,…,m)为蚂蚁k待访问城市的集合,开始时,allowk中有(n-1)个元素,即包括除了蚂蚁k出发城市的其他所有城市,随着时间的推进,allow;中的元素不断减少,直至为空,即表示所有的城市均访问完毕;α为信息素重要程度因子,其值越大,表示信息素的浓度在转移中起的作用越大;β为启发函数重要程度因子,其值越大,表示启发函数在转移中的作用越大,即蚂蚁会以较大的概率转移到距离短的城市。
如前文所述,在蚂蚁释放信息素的同时,各个城市间连接路径上的信息素逐渐消失,设参数ρ(0<ρ<1)表示信息素的挥发程度。因此,当所有蚂蚁完成一次循环后,各个城市间连接路径上的信息素浓度需进行实时更新,即


上述3种模型中,ant cycle system模型利用蚂蚁经过路径的整体信息(经过路径的总长)计算释放的信息素浓度;ant quantity system模型则利用蚂蚁经过路径的局部信息(经过各个城市间的距离)计算释放的信息素浓度;而ant density system模型则更为简单地将信息素释放的浓度取为恒值,并没有考虑不同蚂蚁经过路径长短的影响。因此,一般选用ant cyclesystem模型计算释放的信息素浓度,即蚂蚁经过的路径越短,释放的信息素浓度越高。
1.3 蚁群算法解决TSP问题基本步骤
基于上述原理,将蚁群算法应用于解决TSP问题一般需要以下几个步骤,如图1所示。

图1 蚁群算法解决TSP问题基本步骤
1.初始化参数
在计算之初,需要对相关的参数进行初始化,如蚁群规模(蚂蚁数量)m、信息素重要程度因子α、启发函数重要程度因子β、信息素挥发因子ρ、信息素释放总量Q、最大迭代次数iter_max、迭代次数初值iter=1。
2.构建解空间
将各个蚂蚁随机地置于不同出发点,对每个蚂蚁k(k=1,2,…,m),按照式(22-1)计算其下一个待访问的城市,直到所有蚂蚁访问完所有的城市。
3.更新信息素
计算各个蚂蚁经过的路径长度Lk(k=1,2,…,m),记录当前迭代次数中的最优解(最短路径)。同时,根据式(22-2)和式(22-3)对各个城市连接路径上的信息素浓度进行更新。
4.判断是否终止
若iter<iter_max,则令iter=iter+1,清空蚂蚁经过路径的记录表,并返回步骤2;否则,终止计算,输出最优解。
1.4 蚁群算法的特点
基于蚁群算法的基本思想及解决TSP问题的基本原理,不难发现,与其他优化算法相比,蚁群算法具有以下几个特点:
(1)采用正反馈机制,使得搜索过程不断收敛,最终逼近最优解。
(2)每个个体可以通过释放信息素来改变周围的环境,且每个个体能够感知周围环境的实时变化,个体间通过环境进行间接地通讯。
(3)搜索过程采用分布式计算方式,多个个体同时进行并行计算,大大提高了算法的计算能力和运行效率。
(4)启发式的概率搜索方式不容易陷入局部最优,易于寻找到全局最优解。
2 案例背景
2.1 问题描述
按照枚举法,我国31个直辖市、省会和自治区首府的巡回路径应有约1.326×10^32种,其中一条路径如图2所示。试利用蚁群算法寻找到一条最佳或者较佳的路径。
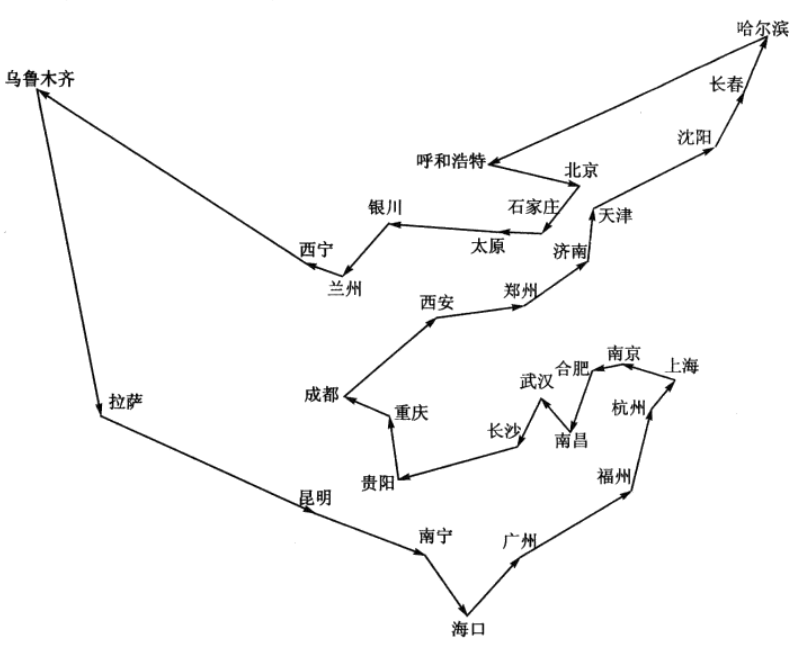
图2我国31个直辖市、省会和自治区首府(未包括我国香港、澳门及台湾)巡回路径
2.2 解题思路及步骤
依据蚁群算法解决TSP问题的基本原理及步骤,实现中国TSP问题求解大体上可以分为以下几个步骤,如图3所示。

图3蚁群算法求解TSP问题一般步骤
1.计算城市间相互距离
根据城市的位置坐标,计算两两城市间的相互距离,从而得到对称的距离矩阵(维数为31的方阵)。需要说明的是,计算出的矩阵对角线上的元素为0,然而如前文所述,由于启发函数ηij(t)=1/dij,因此,为了保证分母不为零,将对角线上的元素修正为一个非常小的正数(如10^(-4)或10^(-5)等)。
2.初始化参数
如前文所述,在计算之前,需要对相关的参数进行初始化,此处不再赘述。
3.迭代寻找最佳路径
首先构建解空间,即各个蚂蚁根据转移概率公式(22-1)访问所有的城市。然后计算各个蚂蚁经过路径的长度,并在每次迭代后根据式(22-2)和式(22-3)实时更新各个城市连接路径上的信息素浓度。经过循环迭代,记录下最优的路径及其长度。
4.结果分析
找到最优路径后,可以将之与其他方法得出的结果进行比较,从而对蚁群算法的性能进行评价。同时,也可以探究不同取值的参数对优化结果的影响,从而找到一组最佳或者较佳的参数组合。
3MATLAB程序实现
利用MATLAB中提供的函数,可以方便地在MATLAB环境下实现上述步骤。
%% 清空环境变量
clear all
clc
%% 导入数据
load citys_data.mat
%% 计算城市间相互距离
n = size(citys,1);
D = zeros(n,n);
for i = 1:n
for j = 1:n
if i ~= j
D(i,j) = sqrt(sum((citys(i,:) - citys(j,:)).^2));
else
D(i,j) = 1e-4;
end
end
end
%% 初始化参数
m = 50; % 蚂蚁数量
alpha = 1; % 信息素重要程度因子
beta = 5; % 启发函数重要程度因子
rho = 0.1; % 信息素挥发因子
Q = 1; % 常系数
Eta = 1./D; % 启发函数
Tau = ones(n,n); % 信息素矩阵
Table = zeros(m,n); % 路径记录表
iter = 1; % 迭代次数初值
iter_max = 200; % 最大迭代次数
Route_best = zeros(iter_max,n); % 各代最佳路径
Length_best = zeros(iter_max,1); % 各代最佳路径的长度
Length_ave = zeros(iter_max,1); % 各代路径的平均长度
%% 迭代寻找最佳路径
while iter <= iter_max
% 随机产生各个蚂蚁的起点城市
start = zeros(m,1);
for i = 1:m
temp = randperm(n);
start(i) = temp(1);
end
Table(:,1) = start;
% 构建解空间
citys_index = 1:n;
% 逐个蚂蚁路径选择
for i = 1:m
% 逐个城市路径选择
for j = 2:n
tabu = Table(i,1:(j - 1)); % 已访问的城市集合(禁忌表)
allow_index = ~ismember(citys_index,tabu);
allow = citys_index(allow_index); % 待访问的城市集合
P = allow;
% 计算城市间转移概率
for k = 1:length(allow)
P(k) = Tau(tabu(end),allow(k))^alpha * Eta(tabu(end),allow(k))^beta;
end
P = P/sum(P);
% 轮盘赌法选择下一个访问城市
Pc = cumsum(P);
target_index = find(Pc >= rand);
target = allow(target_index(1));
Table(i,j) = target;
end
end
% 计算各个蚂蚁的路径距离
Length = zeros(m,1);
for i = 1:m
Route = Table(i,:);
for j = 1:(n - 1)
Length(i) = Length(i) + D(Route(j),Route(j + 1));
end
Length(i) = Length(i) + D(Route(n),Route(1));
end
% 计算最短路径距离及平均距离
if iter == 1
[min_Length,min_index] = min(Length);
Length_best(iter) = min_Length;
Length_ave(iter) = mean(Length);
Route_best(iter,:) = Table(min_index,:);
else
[min_Length,min_index] = min(Length);
Length_best(iter) = min(Length_best(iter - 1),min_Length);
Length_ave(iter) = mean(Length);
if Length_best(iter) == min_Length
Route_best(iter,:) = Table(min_index,:);
else
Route_best(iter,:) = Route_best((iter-1),:);
end
end
% 更新信息素
Delta_Tau = zeros(n,n);
% 逐个蚂蚁计算
for i = 1:m
% 逐个城市计算
for j = 1:(n - 1)
Delta_Tau(Table(i,j),Table(i,j+1)) = Delta_Tau(Table(i,j),Table(i,j+1)) + Q/Length(i);
end
Delta_Tau(Table(i,n),Table(i,1)) = Delta_Tau(Table(i,n),Table(i,1)) + Q/Length(i);
end
Tau = (1-rho) * Tau + Delta_Tau;
% 迭代次数加1,清空路径记录表
iter = iter + 1;
Table = zeros(m,n);
end
%% 结果显示
[Shortest_Length,index] = min(Length_best);
Shortest_Route = Route_best(index,:);
disp(['最短距离:' num2str(Shortest_Length)]);
disp(['最短路径:' num2str([Shortest_Route Shortest_Route(1)])]);
%% 绘图
figure(1)
plot([citys(Shortest_Route,1);citys(Shortest_Route(1),1)],...
[citys(Shortest_Route,2);citys(Shortest_Route(1),2)],'o-');
grid on
for i = 1:size(citys,1)
text(citys(i,1),citys(i,2),[' ' num2str(i)]);
end
text(citys(Shortest_Route(1),1),citys(Shortest_Route(1),2),' 起点');
text(citys(Shortest_Route(end),1),citys(Shortest_Route(end),2),' 终点');
xlabel('城市位置横坐标')
ylabel('城市位置纵坐标')
title(['蚁群算法优化路径(最短距离:' num2str(Shortest_Length) ')'])
figure(2)
plot(1:iter_max,Length_best,'b',1:iter_max,Length_ave,'r:')
legend('最短距离','平均距离')
xlabel('迭代次数')
ylabel('距离')
title('各代最短距离与平均距离对比')
程序运行之前,清除工作空间Workspace中的变量及Command Window中的命令。31个城市的位置坐标(横坐标、纵坐标)保存在citys_data.mat文件中,变量citys为31行2列的数据,第1列表示各个城市的横坐标,第2列表示各个城市的纵坐标。利用城市的横、纵坐标,可以方便地计算出城市间的相互距离。如前文所述,距离矩阵D对角线上的元素设为10^(-4),以便于计算启发函数。计算之前,需要对参数进行初始化。同时,为了加快程序的执行速度,对于程序中涉及的一些过程变量,需要预分配其存储容量。迭代寻找最佳路径为整个算法的核心,首先逐个蚂蚁逐个城市访问,直至遍历所有城市,以构建问题的解空间,然后计算各个蚂蚁经过路径的长度,记录下当前迭代次数中的最佳路径,并实时对各个城市间连接路径上的信息素浓度进行更新,最终经过多次迭代,寻找到最佳路径。
说明:
(1)变量tabu中存储的是已经访问过的城市编号集合,即所谓的“禁忌表”,刚开始时其只存储起始城市编号,随着时间的推进,其中的元素愈来愈多,直至访问到最后一个城市为止。
(2)与变量tabu相反,变量allow中存储的是待访问的城市编号集合,刚开始时其存储了除起始城市编号外的所有城市编号,随着时间的推进,其中的元素愈来愈少,直至访问到最后一个城市为止.
(3)函数ismember用于判断一个变量中的元素是否在另一个变量中出现,具体用法请参考帮助文档,此处不再赘述。
(4)函数cumsum用于求变量中元素的累加和,具体用法请参考帮助文档,此处不再赘述。
(5)计算完城市间的转移概率后,采用与遗传算法中一样的轮盘赌方法选择下一个待访问的城市。
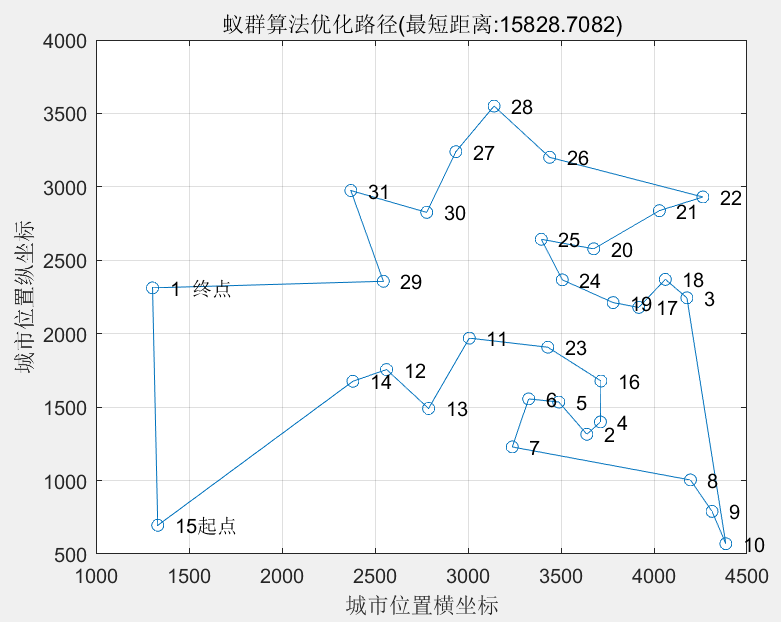
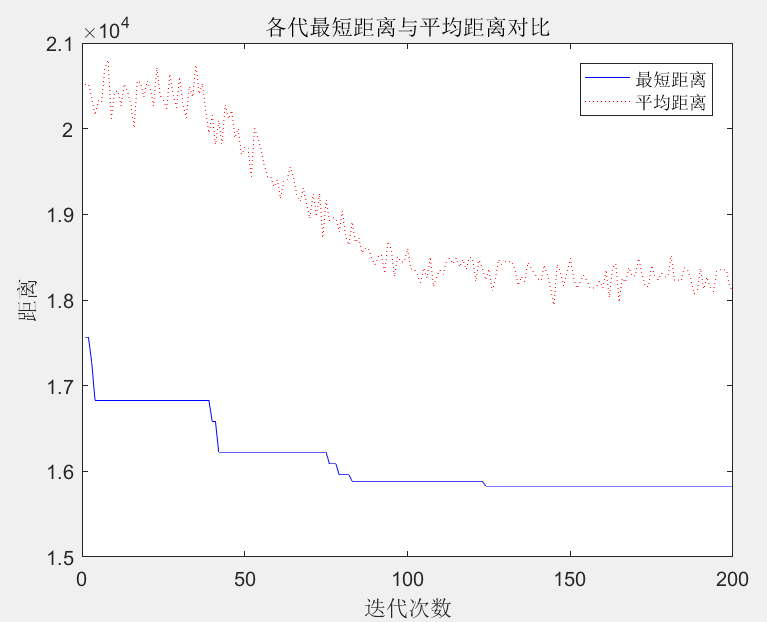
与运行结果对应的路径如图4所示。从图中可以清晰地看到,自起点出发,每个城市访问一次,遍历所有城市后,返回起点。寻找到的最短路径为15828.7082 km。各代的最短距离与平均距离如图5所示,从图中不难发现,随着迭代次数的增加,最短距离与平均距离均呈现不断下降的趋势。当迭代次数大于130时,最短距离已不再变化,表示已经寻找到最佳路径。最新研究成果表明,中国TSP问题的最优解为15377 km,因此,这里寻找到的最佳路径是局部最优解,而并非全局最优解。


4 延伸阅读
4.1 参数的影响及选择
1.蚂蚊个数m对结果的影响
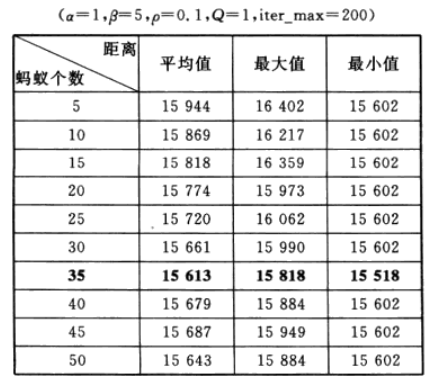
为了探究蚂蚁个数m对最优路径的影响,对比10组不同蚂蚁个数对应的最优路径情况。每组运行20次,结果如表1所列。由表1可以看出,当蚂蚁个数为35时,平均最短路径最短为15613km,此时有最短路径的最小值15518 km。

2.信息素重要程度因子α对结果的影响
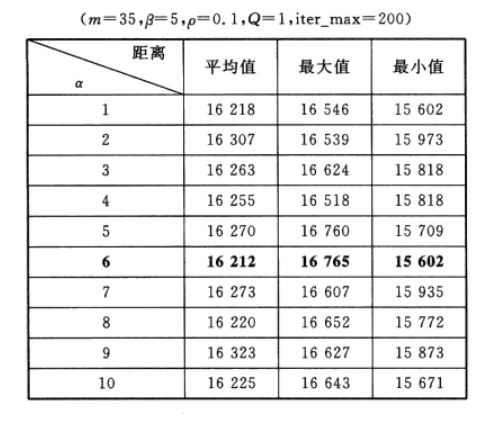
为了研究信息素重要程度因子α对最优路径的影响,对比10组不同α对应的寻找到的最优路径的情况,每组运行20次,结果见表2。可以看出,当α=6时,平均最短路径最小为16212 km。

3.启发函数重要程度因子β对结果的影响
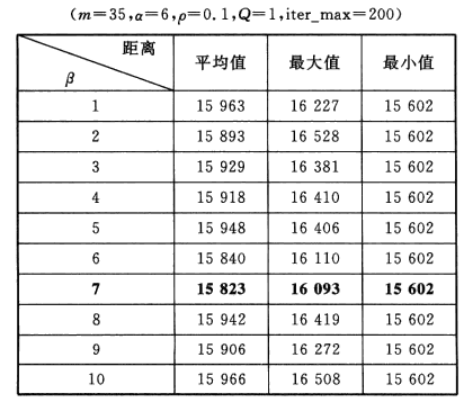
为了研究启发函数重要程度因子β对最优路径的影响,对比10组不同β对应的寻找到的最优路径的情况,每组运行20次,结果如表3所列。由表22-3可以直观地看出,当β=7时,平均最短路径最小为15823km, 此时对应的最短路径为15602 km。

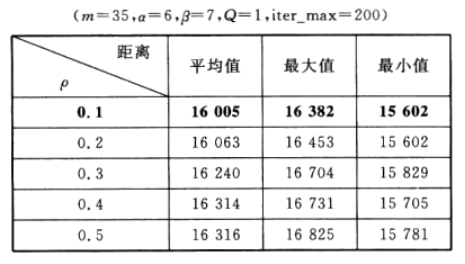
4.信息素挥发因子p对结果的影响
为了研究信息素挥发因子p对最优路径的影响,对比5组不同p对应的寻找到的最优路径的情况,每组运行20次,结果如表4所列。由表4可以直观地看出,当p=0.1时,平均最短路径最小为16005km,此时对应的最短路径为15602 km。
5.信息素释放总量Q对结果的影响
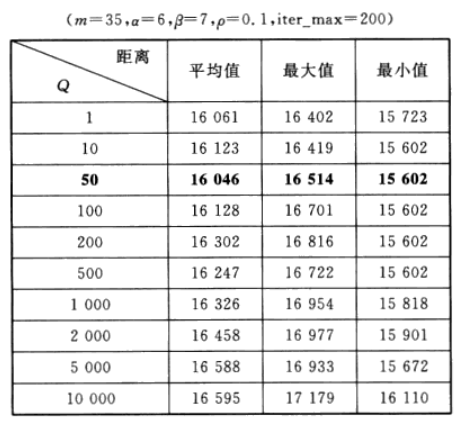
为了研究信息素释放总量Q对最优路径的影响,对比10组不同Q对应的寻找到的最优路径的情况,每组运行20次,结果如表5所列。由表5可以直观地看出,当Q=50时,平均最短路径最小为16046 km,此时对应的最短路径为15602 km。

4.2 总结
蚁群算法以其分布并行式计算、启发式搜索方式等特点,在各个领域中取得了广泛的应用,解决了诸多组合优化方面的难题。针对其可能陷入局部最优的缺点,不少专家和学者提出了许多改进的方法,并将其他算法(如遗传算法、粒子群算法等)与蚁群算法相结合,对蚂蚁个数m、信息素重要程度因子a、启发函数重要程度因子β、信息素挥发因子p、信息素释放总量Q等参数进行优化选择,取得了不错的效果。
5 完整代码获取
完整代码可以从下面的链接中获取:
基于蚁群算法的旅行商问题(TSP)求解(matlab实现)