阵列乘法器

实现乘法的比较常用的方法是类似与手工计算乘法的方式：

对应的硬件结构就是阵列乘法器（array multiplier）它有三个功能：产生部分积，累加部分积和最终相加。

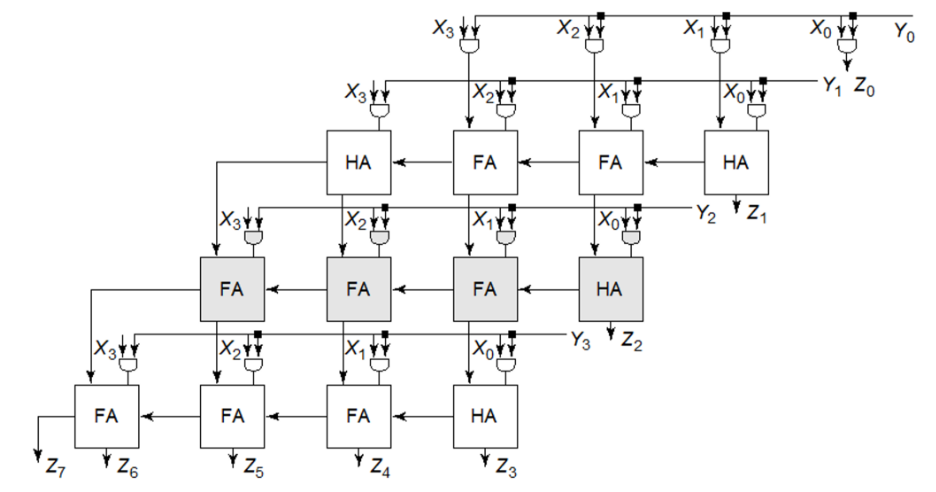
阵列乘法器的关键路径为(下图标出了两条可能的关键路径）：

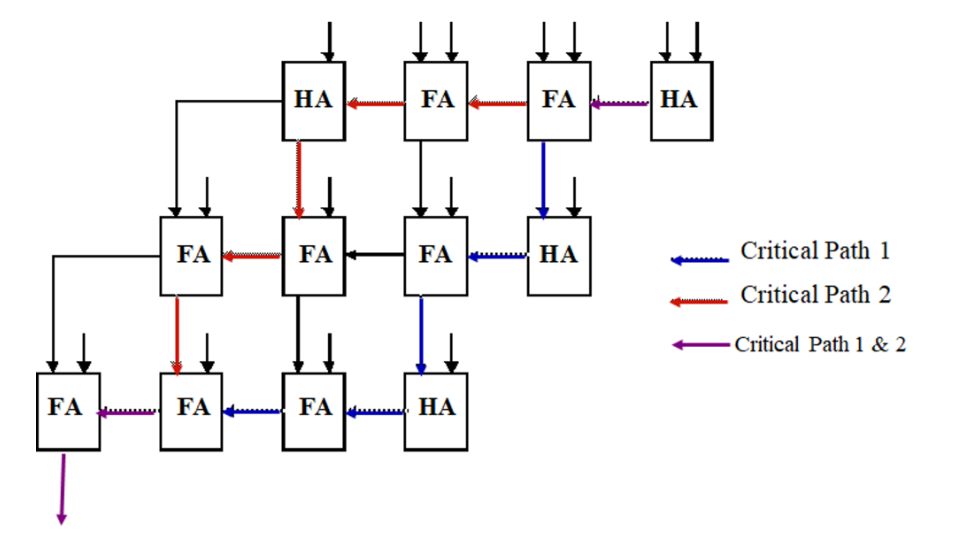
假设乘数为N,被乘数为M。则上面的乘法器产生N个部分积，乘法位数为M,则需要N×M个二输入AND门以及N−1个M位加法器。可以得到关键路径延时为：

$$t_{mult}=[(M-1)+(N-2)]t_{carry}+(N-1)t_{sum}+t_{and}$$

进位保留乘法器

背景：由于阵列乘法器中有许多几乎一样的关键路径，因此通过调整晶体管的尺寸来提高性能效果有限。

解决：进位输出可以沿着对角线传播而不是向左传递，这样传播并不改变结果，只需要加入额外的一排加法器（向量合并加法器vector-merging)来产生最终的结果。这样的乘法器叫做进位保留乘法器：

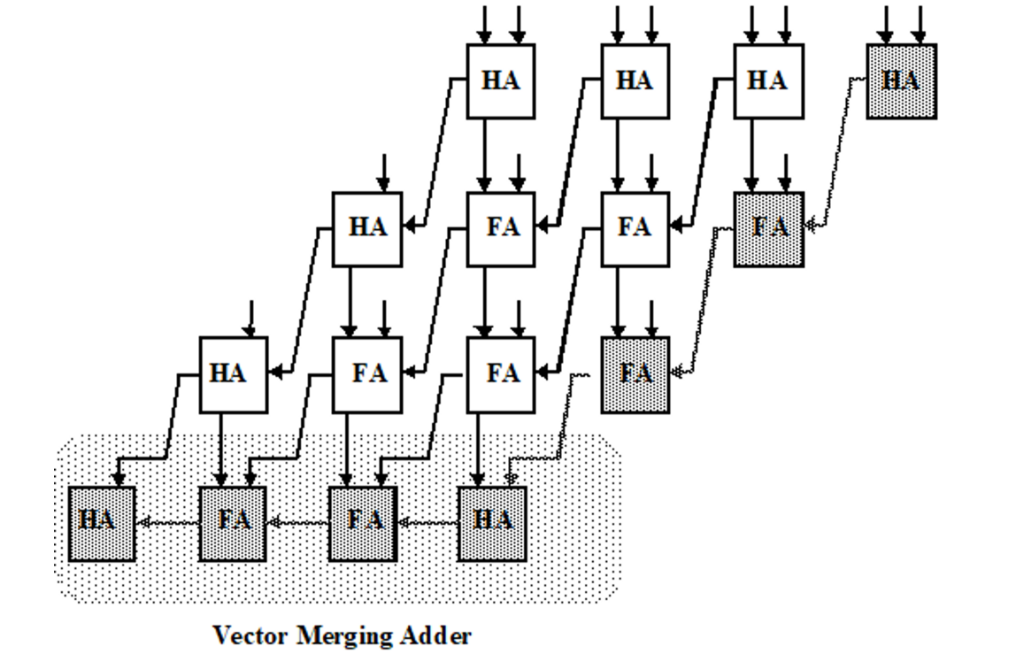
其关键路径为图中灰色部分，且只有一条。 其传播延时为：

$$t_{mult}=t_{and}+(N-1)t_{carry}+t_{merge}$$

可见，相比于阵列乘法器，进位保留乘法器增加了部分面积，但关键路径唯一确定。

下图是进位保留加法器的布图（floorplan)结构。其规整的结构适合自动化生成。

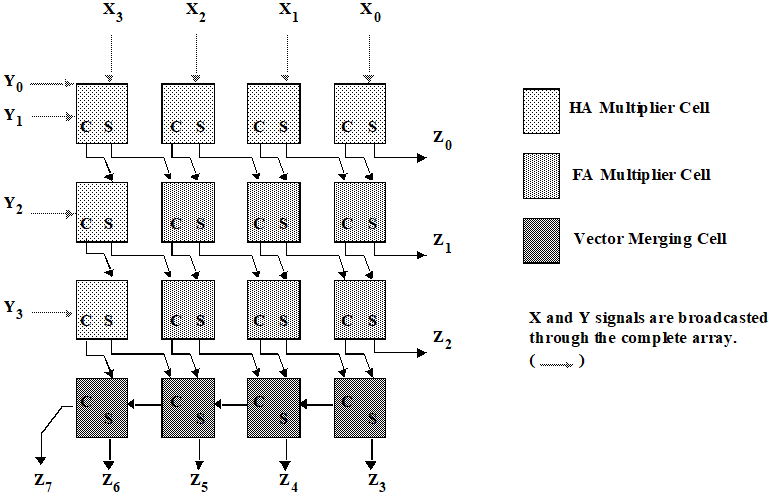
树形乘法器

部分积的求和加法器可以安排为树形以减少关键路径和减少加法器。其中两个点的是半加器，三个点的是全加器。其压缩过程可以分为下面几步：

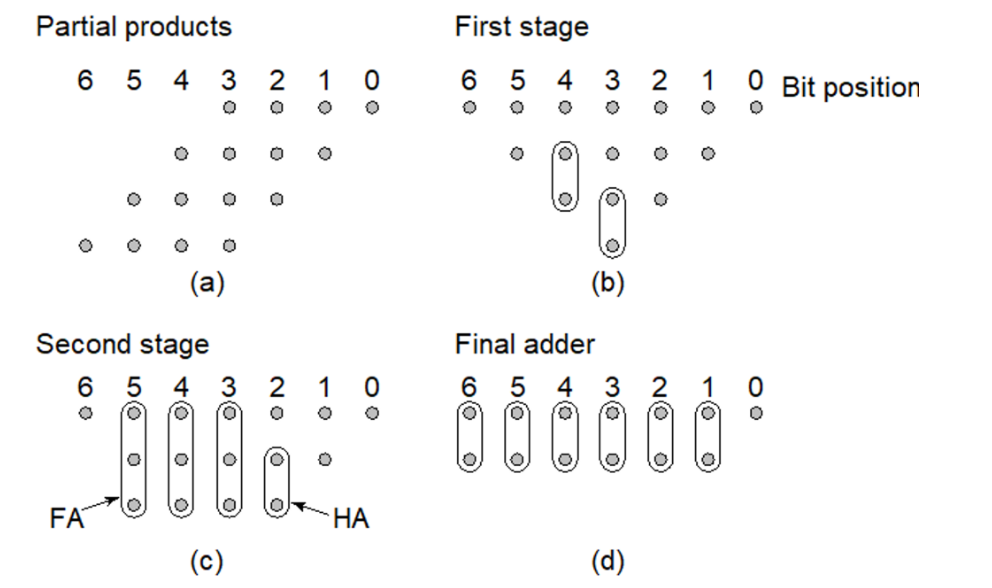
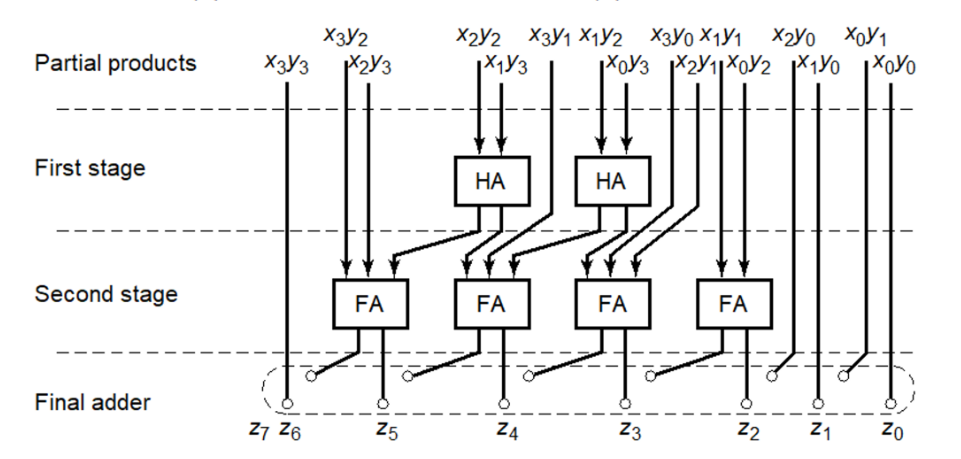
可见，前面的两部只需要三个半加器和三个全加器，最后一步是简单的加法器链。只比较前面部分的话，进位保留加法器的前面部分需要6个全加器和6个半加器！优点：除了节省乘法器需要的硬件，Wallace树形乘法器也可以减少传播延时，其延时$O(lo{g}_{1.5}(N))$。

缺点： 非常不规则，版图设计复杂。

Booth乘法器

假设A和B是乘数和被乘数，且有：

$$\begin{array}{rl}A& =a_{n-1}{a}_{n-2}\dots a_1{a}_0\\ B& =b_{n-1}{b}_{n-2}\dots b_1{b}_0\\ A\ast B& =(0-a_0)\times B\times 2^0+(a_0-a_1)\times B\times 2^1+\\ & (a_1-a_2)\times B\times 2^2+\cdots +(a_{n-2}-a_{n-1})\times B\times 2^n-1\\ & =B\times [-a_{n-1}\times 2^{n-1}+\sum _{i=0}^{n-2}{a}_i\times 2^i]\\ & =B\times Val(A)\end{array}$$

上述是以补码形式进行的

上面的公式推导了booth乘法对乘数的分解原理，实际上在编码时只需要公式3，可以做如下的编码表：

$a_i$	$a_{i-1}$	$a_{i-1}-a_i$	操作
0	0	0	+0，右移一位
1	0	-1	减B,右移一位
1	1	0	+0,右移一位
0	1	1	加B,右移一位

例： $N=7,B=22=(0010110{)}_2,A=-34=-(0100010{)}_2$

首先计算-B的补码(算法中要用到）： $\overline{-B}=(1101010{)}_2$以及A的补码： $\overline{A}=(1011110{)}_2$

硬件计算过程如下：

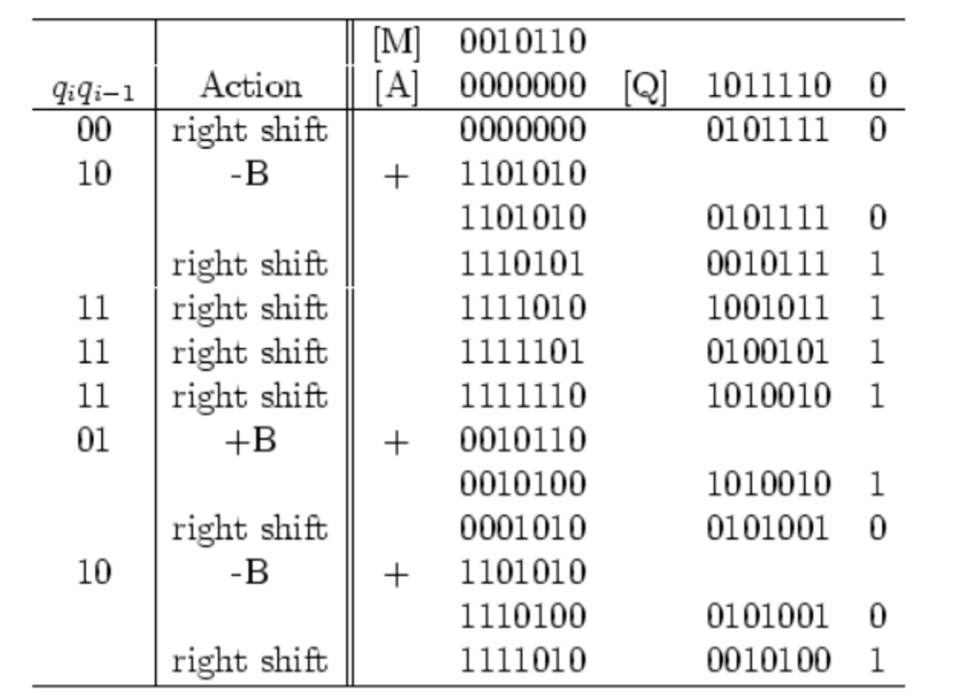
1、被乘数B与乘数A均以补码的形式参加乘法运算，运算结果是积的补码 。

2、部分积和被乘数B采用双符号位，乘数A采用单符号位 。

3、初始部分积为0。运算前，在乘数A的补码末位添加一位附加位An+1，初始值为0 。

4、根据AnAn+1的值，按照上表进行累加右移操作，右移时遵循补码的移位规则 。

5、累加n+1次，右移n次，最后一次不右移 。

6、实际上，对于公式中的每一项 $(a_{i-1}-a_i)\times B\times 2^i$都对应实际算法中的每一步。 $(a_{i-1}-a_i)$决定了B的系数，右移操作因为作用在[A][Q]寄存器上，所以实际上是相当于将积右移，等价于B左移，所以这一步对应 $\times 2^i$操作。加减B的操作都作用在[A]寄存器上，保证了 $\times 2^i$后的B能够作用在正确的位上。

基2booth乘法器设计

`timescale 1ns/1ps
module booth_fsm
# (parameter DATAWIDTH = 8)
(
  input                        clk,
  input                        rstn,
  input                        en,
  input        [DATAWIDTH-1:0] multiplier,                            
  input        [DATAWIDTH-1:0] multiplicand,
  output reg                   done,
  output reg [2*DATAWIDTH-1:0] product
);

parameter   IDLE   = 2'b00,
            ADD    = 2'b01,
            SHIFT  = 2'b11,
            OUTPUT = 2'b10;

reg  [1:0]              current_state, next_state;  // state registers.
reg  [2*DATAWIDTH+1:0]  a_reg,s_reg,p_reg,sum_reg;  // computational values.
reg  [DATAWIDTH-1:0]    iter_cnt;                   // iteration count for determining when done.
wire [DATAWIDTH:0]      multiplier_neg;             // negative value of multiplier

always @(posedge clk or negedge rstn)
  if (!rstn) current_state = IDLE;
  else current_state <= next_state;

// state transform
always @(*) begin
  next_state = 2'bx;
  case (current_state)
    IDLE  : if (en) next_state = ADD;
            else    next_state = IDLE;
    ADD   : next_state = SHIFT;
    SHIFT : if (iter_cnt==DATAWIDTH) next_state = OUTPUT;
            else            next_state = ADD;
    OUTPUT: next_state = IDLE;
  endcase
end

// negative value of multiplier.
assign multiplier_neg = -{multiplier[DATAWIDTH-1],multiplier}; 
// algorithm implemenation details.
always @(negedge clk or negedge rstn) begin
  if (!rstn) begin
    {a_reg,s_reg,p_reg,iter_cnt,done,sum_reg,product} <= 0;
  end else begin
  case (current_state)
    IDLE :  begin
      a_reg    <= {multiplier[DATAWIDTH-1],multiplier,{(DATAWIDTH+1){1'b0}}};
      s_reg    <= {multiplier_neg,{(DATAWIDTH+1){1'b0}}};
      p_reg    <= {{(DATAWIDTH+1){1'b0}},multiplicand,1'b0};
      iter_cnt <= 0;
      done     <= 1'b0;
    end
    ADD  :  begin
      case (p_reg[1:0])
        2'b01       : sum_reg <= p_reg+a_reg; // + multiplier
        2'b10       : sum_reg <= p_reg+s_reg; // - multiplier
        2'b00,2'b11 : sum_reg <= p_reg;       // nop
      endcase
      iter_cnt <= iter_cnt + 1;
    end
    SHIFT :  begin
      p_reg <= {sum_reg[2*DATAWIDTH+1],sum_reg[2*DATAWIDTH+1:1]}; // right shift 
    end
    OUTPUT : begin
      product <= p_reg[2*DATAWIDTH:1];
      done <= 1'b1;
    end
  endcase
 end
end

endmodule

testbench:

`timescale 1ns/1ps

// Basic exhaustive self checking test bench.
`define TEST_WIDTH 10
module booth_fsm_tb;

reg clk;
reg rstn;
reg en;
//integer multiplier1;
//integer multiplicand1;
reg [`TEST_WIDTH-1:0] multiplier;
reg [`TEST_WIDTH-1:0] multiplicand;
wire    done;

//输入 ：要定义有符号和符号，输出：无要求
wire signed [2*`TEST_WIDTH-1:0] product;
wire signed [`TEST_WIDTH-1:0]                m1_in;
wire signed [`TEST_WIDTH-1:0]                m2_in;

reg  signed [2*`TEST_WIDTH-1:0] product_ref;
reg  [2*`TEST_WIDTH-1:0] product_ref_u;
assign m1_in = multiplier[`TEST_WIDTH-1:0];
assign m2_in = multiplicand[`TEST_WIDTH-1:0];

booth_fsm #(.DATAWIDTH(`TEST_WIDTH)) booth 
(
  .clk(clk),
  .rstn(rstn),
  .en(en),
  .multiplier(multiplier),                            
  .multiplicand(multiplicand),
  .done  (done),
  .product(product)
 );

always #1 clk = ~clk;

integer num_good;
integer i;
initial begin
  clk = 1;
  en = 0;
  rstn = 1;
  #2 rstn = 0; #2 rstn = 1;
  
  num_good = 0;
  multiplier=0;
  multiplicand=0;
  #8;

  for(i=0;i<4;i=i+1) begin
    en = 1;
    multiplier=10'b10000_00000+i;
    multiplicand=10'b00000_00010+i;

    wait (done == 0);
    wait (done == 1);
	product_ref=m1_in*m2_in;
    product_ref_u=m1_in*m2_in;
    if (product_ref !== product) 
         $display("multiplier = %d multiplicand = %d proudct =%d",m1_in,m2_in,product);
        @(posedge clk);
  end		
  $display("sim done. num good = %d",num_good);

end

initial begin
	$fsdbDumpfile("tb.fsdb");
    $fsdbDumpvars();
    $fsdbDumpMDA();
    $dumpvars();
    #1000 $finish;
 end
endmodule

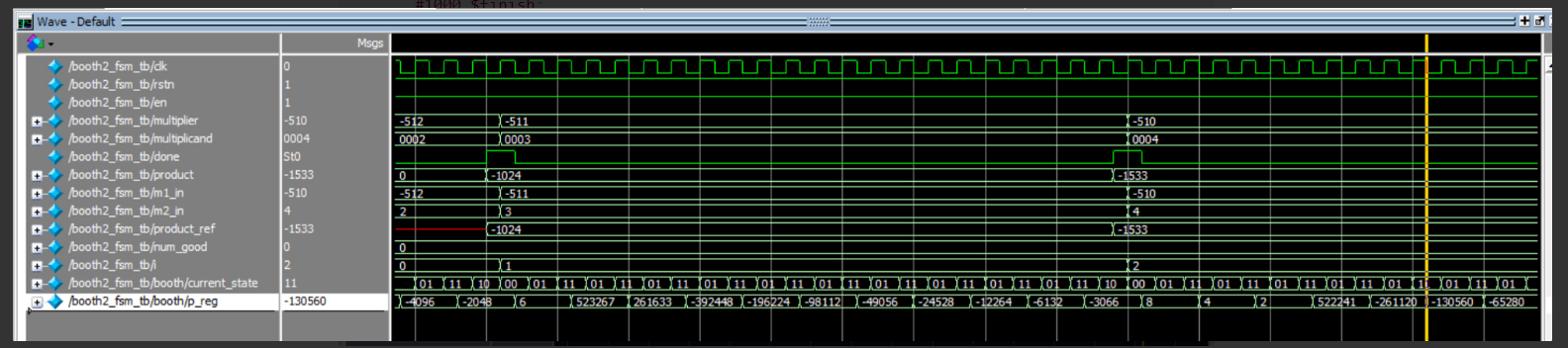
仿真波形: