神经网络

感知机的缺点是需要人工设定即确定合适的、能符合预期的输入与输出的权重，而神经网络可以自动地从数据中学习到合适的权重参数。

从感知机到神经网络

神经网络的例子

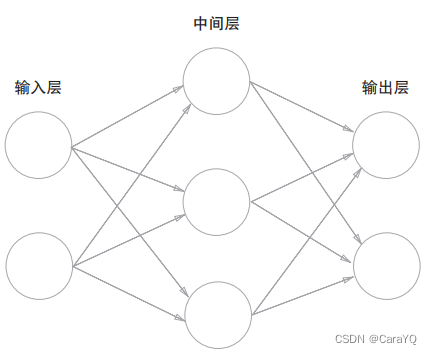
本书约定：

1. 图3-1中，第0层对应输入层，第1层对应中间层，第2层对应输出层
   图3-1中的网络一共由3层神经元构成，但实质上只有2层神经元有权重，因此将其称为“2层网络”。有的书也会根据构成网络的层数，把图 3-1的网络称为3层网络。本书将根据
   实质上拥有权重的层数（输入层、隐藏层、输出层的总数减去 1后的数量）来表示网络的名称。

复习感知机

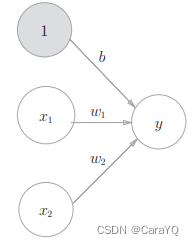
图3-2中的感知机接收x1、x2、1三个输入信号，输出y。b是被称为偏置的参数，用于控制神经元被激活的容易程度；而w1和w2是表示各个信号的权重的参数，用于控制各个信号的重要性。用数学式来表示则如式（3.1）所示

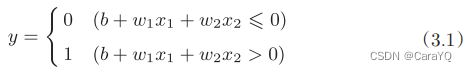
图3-2将x1、x2、1三个信号作为神经元的输入，将其和各自的权重相乘后，传送至下一个神经元。在下一个神经元中，计算这些加权信号的总和。如果这个总和超过0，则输出1，否则输出0，我们用一个函数来表示这种分情况的动作，引入新函数h(x)，将式（3.1）改写成下面的式（3.2）和式（3.3）。

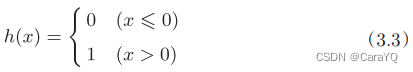
激活函数登场

刚才登场的h（x）函数会将输入信号的总和转换为输出信号，这种函数一般称为激活函数，用于决定如何来激活输入信号的总和。
如果将式（3.2）写得详细一点，则可以分成下面两个式子：

如果要在图中明确表示出式（3.4）和式（3.5），则可以像图3-4这样做。

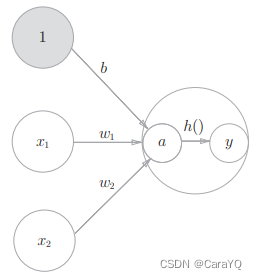
如图3-4所示，表示神经元的○中明确显示了激活函数的计算过程，即信号的加权总和为神经元a，然后神经元a被激活函数h()转换成神经元y

激活函数是连接感知机和神经网络的桥梁。本书在使用“感知机”一词时，没有严格统一它所指的算法。一般而言，“朴素感知机”是指单层网络，指的是激活函数使用了阶跃函数A 的模型。“多层感知机”是指神经网络，即使用 sigmoid函数（后述）等平滑的激活函数的多层网络。

激活函数

式（3.3）表示的激活函数以阈值为界，一旦输入超过阈值，就切换输出。这样的函数称为“阶跃函数”。因此，可以说感知机中使用了阶跃函数作为激活函数。如果将激活函数从阶跃函数换成其他函数，就可以进入神经网络的世界了。下面我们就来介绍一下神经网络使用的激活函数

sigmoid函数

神经网络中经常使用的一个激活函数就是式（3.6）表示的sigmoid函数

阶跃函数的实现

阶跃函数如式（3.3）所示，当输入超过0时，输出1，否则输出0。可以像下面这样简单地实现阶跃函数。

def step_function(x):
 if x > 0:
 return 1
 else:
 return 0

上述实现中，参数x只能接受实数（浮点数），不允许参数取NumPy数组。为了便于后面的操作，我们把它修改为支持NumPy数组的实现，先准备一个NumPy数组x，并对这个NumPy数组进行了不等号运算。

>>> import numpy as np
>>> x = np.array([-1.0, 1.0, 2.0])
>>> x
array([-1., 1., 2.])
>>> y = x > 0
>>> y
array([False, True, True], dtype=bool)

对NumPy数组进行不等号运算后，数组的各个元素都会进行不等号运算，生成一个布尔型数组。这里，数组x中大于0的元素被转换为True，小于等于0的元素被转换为False，从而生成一个新的数组y。
数组y是一个布尔型数组，但是我们想要的阶跃函数是会输出int型的0或1的函数。因此，需要把数组y的元素类型从布尔型转换为int型。

>>> y = y.astype(np.int)
>>> y
array([0, 1, 1])

如上所示，可以用astype()方法转换NumPy数组的类型。astype()方法通过参数指定期望的类型，这个例子中是np.int型。Python中将布尔型转换为int型后，True会转换为1，False会转换为0

sigmoid函数的实现

def sigmoid(x):
 return 1 / (1 + np.exp(-x))

参数x为NumPy数组时，结果也能被正确计算，这是因为NumPy的广播功能

sigmoid函数和阶跃函数的比较

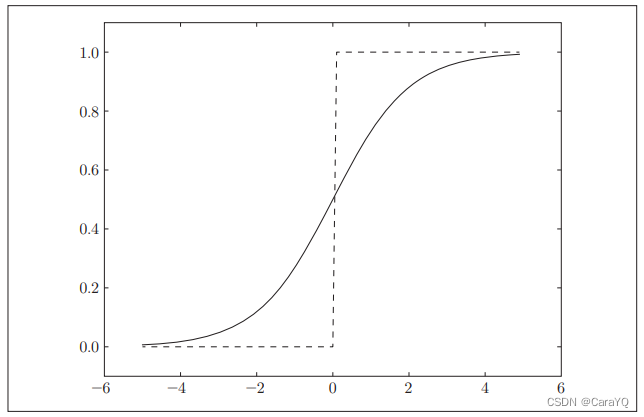
相同点：

1. 具有相似的形状。实际上，两者的结构均是“输入小时，输出接近0（为0）；随着输入增大，输出向1靠近（变成1）”。也就是说，当输入信号为重要信息时，阶跃函数和sigmoid函数都会输出较大的值；当输入信号为不重要的信息时，两者都输出较小的值。
2. 不管输入信号有多小，或者有多大，输出信号的值都在0到1之间
3. 两者均为非线性函数。

神经网络的激活函数必须使用非线性函数。因为使用线性函数的话，加深神经网络的层数就没有意义了。线性函数的问题在于，不管如何加深层数，总是存在与之等效的“无隐藏层的神经网络”。

不同点：

1. “平滑性”的不同。sigmoid函数是一条平滑的曲线，输出随着输入发生连续性的变化。而阶跃函数以0为界，输出发生急剧性的变化。
2. 相对于阶跃函数只能返回0或1，sigmoid函数可以返回0.731 …、0.880 …等实数（这一点和刚才的平滑性有关）。也就是说，感知机中神经元之间流动的是0或1的二元信号，而神经网络中流动的是连续的实数值信号。

ReLU函数

在神经网络发展的历史上，sigmoid函数很早就开始被使用了，而最近则主要使用ReLU（Rectified Linear Unit）函数。ReLU函数在输入大于0时，直接输出该值；在输入小于等于0时，输
出0（图3-9）。ReLU函数可以表示为下面的式(3.7)。


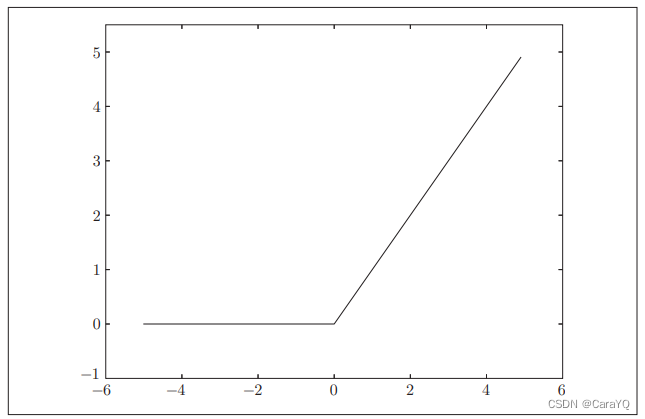
ReLU函数的实现：

def relu(x):
 return np.maximum(0, x)

3层神经网络的实现

符号确认

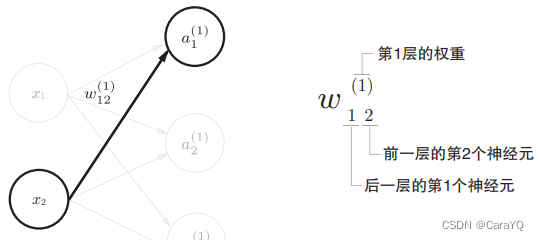
权重和隐藏层的神经元的右上角有一个“(1)”，它表示权重和神经元的层号（即第1层的权重、第1层的神经元）。此外，权重的右下角有两个数字，它们是后一层的神经元和前一层的神经元的索引号。

代码实现

# 保存每一层所需的参数（权重和偏置）
def init_network():
 network = {}
 network['W1'] = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])
 network['b1'] = np.array([0.1, 0.2, 0.3])
 network['W2'] = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]])
 network['b2'] = np.array([0.1, 0.2])
 network['W3'] = np.array([[0.1, 0.3], [0.2, 0.4]])
network['b3'] = np.array([0.1, 0.2])
 return network
def forward(network, x):
 W1, W2, W3 = network['W1'], network['W2'], network['W3']
 b1, b2, b3 = network['b1'], network['b2'], network['b3']
 a1 = np.dot(x, W1) + b1
 z1 = sigmoid(a1)
 a2 = np.dot(z1, W2) + b2
 z2 = sigmoid(a2)
 a3 = np.dot(z2, W3) + b3
 y = identity_function(a3)
 return y
network = init_network()
x = np.array([1.0, 0.5])
y = forward(network, x)
print(y) # [ 0.31682708 0.69627909]

输出层的设计

神经网络可以用在分类问题和回归问题上，不过需要根据情况改变输出层的激活函数。一般而言，回归问题用恒等函数，分类问题用softmax函数。

机器学习的问题大致可以分为分类问题和回归问题。分类问题是数据属于哪一个类别的问题。比如，区分图像中的人是男性还是女性的问题就是分类问题。而回归问题是根据某个输入预测一个（连续的）数值的问题。比如，根据一个人的图像预测这个人的体重的问题就是回归问题（类似“57.4kg”这样的预测）

恒等函数和softmax函数

恒等函数会将输入按原样输出，对于输入的信息，不加以任何改动地直接输出。
分类问题中使用的softmax函数可以用下面的式（3.10）表示，其输出可以理解为“概率”

实现softmax函数

>>> a = np.array([0.3, 2.9, 4.0])
>>>
>>> exp_a = np.exp(a) # 指数函数
>>> print(exp_a)
[ 1.34985881 18.17414537 54.59815003]
>>>
>>> sum_exp_a = np.sum(exp_a) # 指数函数的和
>>> print(sum_exp_a)
74.1221542102
>>>
>>> y = exp_a / sum_exp_a
>>> print(y)
[ 0.01821127 0.24519181 0.73659691]

上面的实现虽然正确描述了式（3.10），但在计算机的运算上可能出现溢出问题。softmax函数的实现中要进行指数函数的运算，但是此时指数函数的值很容易变得非常大。比如，e10的值会超过20000，e100会变成一个后面有40多个0的超大值，e1000的结果会返回一个表示无穷大的inf。如果在这些超大值之间进行除法运算，结果会出现“不确定”的情况。据此，我们做以下改进：

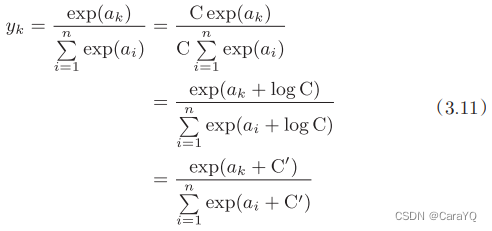
首先，式（3.11）在分子和分母上都乘上C这个任意的常数。然后，把这个C移动到指数函数（exp）中，记为log C。最后，把log C替换为另一个符号C’。式（3.11）说明，在进行softmax的指数函数的运算时，加上（或者减去）某个常数并不会改变运算的结果。这里的C’可以使用任何值，但是为了防止溢出，一般会使用输入信号中的最大值。综上，我们可以像下面这样实现softmax函数。

def softmax(a):
 c = np.max(a)
 exp_a = np.exp(a - c) # 溢出对策
 sum_exp_a = np.sum(exp_a)
 y = exp_a / sum_exp_a
 return y

一般而言，神经网络只把输出值最大的神经元所对应的类别作为识别结果。并且，即便使用softmax函数，输出值最大的神经元的位置也不会变。因此，神经网络在进行分类时，输出层的softmax函数可以省略。在实际的问题中，由于指数函数的运算需要一定的计算机运算量，因此输出层的softmax函数一般会被省略。

求解机器学习问题的步骤可以分为“学习”A 和“推理”两个阶段。首先，在学习阶段进行模型的学习B，然后，在推理阶段，用学到的模型对未知的数据进行推理（分类）。如前所述，推理阶段一般会省略输出层的 softmax函数。在输出层使用 softmax函数是因为它和神经网络的学习有关系

输出层的神经元数量

对于分类问题，输出层的神经元数量一般设定为类别的数量。

手写数字识别

和求解机器学习问题的步骤（分成学习和推理两个阶段进行）一样，使用神经网络解决问题时，也需要首先使用训练数据（学习数据）进行权重参数的学习；进行推理时，使用刚才学习到的参数，对输入数据进行分类，推理处理也称为神经网络的前向传播

MNIST数据集

MNIST数据集的一般使用方法是，先用训练图像进行学习，再用学习到的模型度量能在多大程度上对测试图像进行正确的分类。MNIST的图像数据是28像素 × 28像素的灰度图像（1通道），各个像素
的取值在0到255之间。每个图像数据都相应地标有“7”“2”“1”等标签。
本书提供了便利的Python脚本mnist.py，该脚本支持从下载MNIST数据集到将这些数据转换成NumPy数组等处理（mnist.py在dataset目录下），使用mnist.py中的load_mnist()函数，就可以按下述方式轻松读入MNIST数据。

import sys, os
sys.path.append(os.pardir) # 为了导入父目录中的文件而进行的设定
from dataset.mnist import load_mnist
# 第一次调用会花费几分钟 ……
(x_train, t_train), (x_test, t_test) = load_mnist(flatten=True,
normalize=False)
# 输出各个数据的形状
print(x_train.shape) # (60000, 784)
print(t_train.shape) # (60000,)
print(x_test.shape) # (10000, 784)
print(t_test.shape) # (10000,)

上述代码在mnist_show.py文件中。mnist_show.py文件的当前目录是ch03，但包含load_mnist()函数的mnist.py文件在dataset目录下。因此，mnist_show.py文件不能跨目录直接导入mnist.py文件。sys.path.append(os.pardir)语句实际上是把父目录deep-learning-from-scratch加入到sys.path（Python的搜索模块的路径集）中，从而可以导入deep-learning-from-scratch下的任何目录（包括dataset目录）中的任何文件
load_mnist函数以“(训练图像 ,训练标签 )，(测试图像，测试标签 )”的形式返回读入的MNIST数据。此外，还可以像load_mnist(normalize=True, flatten=True, one_hot_label=False) 这 样，设 置 3 个 参 数。第 1 个参数normalize设置是否将输入图像正规化为0.0～1.0的值。如果将该参数设置为False，则输入图像的像素会保持原来的0～255。第2个参数flatten设置是否展开输入图像（变成一维数组）。如果将该参数设置为False，则输入图像为1 × 28 × 28的三维数组；若设置为True，则输入图像会保存为由784个元素构成的一维数组。第3个参数one_hot_label设置是否将标签保存为one-hot表示（one-hot representation）。one-hot表示是仅正确解标签为1，其余皆为0的数组，就像[0,0,1,0,0,0,0,0,0,0]这样。当one_hot_label为False时，只是像7、2这样简单保存正确解标签；当one_hot_label为True时，标签则保存为one-hot表示

Python有 pickle这个便利的功能。这个功能可以将程序运行中的对象保存为文件。如果加载保存过的 pickle文件，可以立刻复原之前程序运行中的对象。用于读入MNIST数据集的load_mnist()函数内部也使用了 pickle功能（在第 2次及以后读入时）。利用 pickle功能，可以高效地完成MNIST数据的准备工作。

显示一张MNIST图像（源代码在ch03/mnist_show.py中）

import sys, os
sys.path.append(os.pardir)
import numpy as np
from dataset.mnist import load_mnist
from PIL import Image
def img_show(img):
 pil_img = Image.fromarray(np.uint8(img))
 pil_img.show()
(x_train, t_train), (x_test, t_test) = load_mnist(flatten=True,
normalize=False)
img = x_train[0]
label = t_train[0]
print(label) # 5
print(img.shape) # (784,)
img = img.reshape(28, 28) # 把图像的形状变成原来的尺寸
print(img.shape) # (28, 28)
img_show(img)

这里需要注意的是，flatten=True时读入的图像是以一列（一维）NumPy数组的形式保存的。因此，显示图像时，需要把它变为原来的28像素 × 28像素的形状。可以通过reshape()方法的参数指定期望的形状，更改NumPy数组的形状。此外，还需要把保存为NumPy数组的图像数据转换为PIL用的数据对象，这个转换处理由Image.fromarray()来完成。

神经网络的推理处理

6.13号前，周一

开始述职，周末写好
7分钟=5分钟履职+2分钟计划